Multiply matrices of complex numbers using NumPy in Python

In this article, we will discuss how to multiply two matrices containing complex numbers using NumPy but first, let’s know what is a complex number. A Complex Number is any number that can be represented in the form of x+yj where x is the real part and y is the imaginary part. Multiplication of two complex numbers can be done using the below formula – 

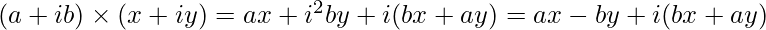
NumPy provides the vdot() method that returns the dot product of vectors a and b. This function handles complex numbers differently than dot(a, b).

Syntax:

numpy.vdot(vector_a, vector_b)

Example 1:

Python3

# importing numpy as library
import numpy as np


# creating matrix of complex number
x = np.array([2+3j, 4+5j])
print("Printing First matrix:")
print(x)

y = np.array([8+7j, 5+6j])
print("Printing Second matrix:")
print(y)

# vector dot product of two matrices
z = np.vdot(x, y)
print("Product of first and second matrices are:")
print(z)

Output:

Printing First matrix:
[2.+3.j 4.+5.j]
Printing Second matrix:
[8.+7.j 5.+6.j]
Product of first and second matrices are:
(87-11j)

Time complexity: O(1)
Auxiliary space: O(1)

Example 2: Now suppose we have 2D matrix: 

Python3

# importing numpy as library
import numpy as np


# creating matrix of complex number
x = np.array([[2+3j, 4+5j], [4+5j, 6+7j]])
print("Printing First matrix:")
print(x)

y = np.array([[8+7j, 5+6j], [9+10j, 1+2j]])
print("Printing Second matrix:")
print(y)

# vector dot product of two matrices
z = np.vdot(x, y)
print("Product of first and second matrices are:")
print(z)

Output:

Printing First matrix:
[[2.+3.j 4.+5.j]
 [4.+5.j 6.+7.j]]
Printing Second matrix:
[[8. +7.j 5. +6.j]
 [9.+10.j 1. +2.j]]
Product of first and second matrices are:
(193-11j)

Time complexity: O(n^2), where n is the dimension of the matrices.
Auxiliary space: O(1), as the matrices and their product are stored in memory and no additional space is used.