Multiple Linear Regression Model with Normal Equation
Last Updated :
08 May, 2021
Prerequisite: NumPy
Consider a data set,
| area (x1) | rooms (x2) | age (x3) | price (y) |
| 23 | 3 | 8 | 6562 |
| 15 | 2 | 7 | 4569 |
| 24 | 4 | 9 | 6897 |
| 29 | 5 | 4 | 7562 |
| 31 | 7 | 6 | 8234 |
| 25 | 3 | 10 | 7485 |
let us consider,
Here area, rooms, age are features / independent variables and price is the target / dependent variable. As we know the hypothesis for multiple linear regression is given by:
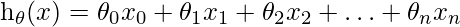

where, 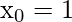
NOTE: Here our target is to find the optimum value for the parameters θ. To find the optimum value for θ we can use the normal equation. So after finding the values for θ, our linear hypothesis or linear model will be ready to predict the price for new features or inputs.
Normal Equation is :
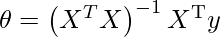
Considering the above data set we can write,
X: an array of all independent features with size (n x m) where m is a total number of training samples and n is the total number of features including (x0 = 1)
XT: Transpose of array X
y: y is 1D array/column array/vector of target/dependent variable with size m where m is a total number of training samples.
So for the above example we can write :
X = [[ 1, 23, 3, 8],
[ 1, 15, 2, 7],
[ 1, 24, 4, 9],
[ 1, 29, 5, 4],
[ 1, 31, 7, 6],
[ 1, 25, 3, 10]]
X T= [[ 1, 1, 1, 1, 1, 1],
[23, 15, 24, 29, 31, 25],
[ 3, 2, 4, 5, 7, 3],
[ 8, 7, 9, 4, 6, 10]]
y= [6562, 4569, 6897, 7562, 8234, 7485]
Code: Implementation of Linear Regression Model with Normal Equation
Python
import numpy as np
class LinearRegression:
def __init__(self):
pass
def __compute(self, x, y):
try:
self.__thetas = np.dot(np.dot(np.linalg.inv(np.dot(x.T,x)),x.T),y)
except Exception as e:
raise e
def fit(self, x, y):
x = np.array(x)
ones_ = np.ones(x.shape[0])
x = np.c_[ones_,x]
y = np.array(y)
self.__compute(x,y)
@property
def coef_(self):
return self.__thetas[0]
@property
def intercept_(self):
return self.__thetas[1:]
def predict(self, x):
try:
x = np.array(x)
ones_ = np.ones(x.shape[0])
x = np.c_[ones_,x]
result = np.dot(x,self.__thetas)
return result
except Exception as e:
raise e
x_train = [[2,40],[5,15],[8,19],[7,25],[9,16]]
y_train = [194.4, 85.5, 107.1, 132.9, 94.8]
x_test = [[12,32],[2,40]]
y_test = []
lr = LinearRegression()
lr.fit(x,y)
print(lr.coef_,lr.intercept_)
print(lr.predict(x_t))
|
Output :
Value of Intercept = 305.3333333334813
Coefficients are = [236.85714286 -4.76190476 102.9047619 ]
Actual value of Test Data = [8234, 7485]
Predicted value of Test Data = [8232. 7241.52380952]
Share your thoughts in the comments
Please Login to comment...