Minimum product of k integers in an array of positive Integers
Last Updated :
18 Jan, 2024
Given an array of n positive integers. We are required to write a program to print the minimum product of k integers of the given array.
Examples:
Input : 198 76 544 123 154 675
k = 2
Output : 9348
We get minimum product after multiplying
76 and 123.
Input : 11 8 5 7 5 100
k = 4
Output : 1400
An approach using Sorting:
- Sort the array in increasing order.
- Take the product of the first K elements of the array
- Return the result.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minProduct(int arr[], int n, int k)
{
sort(arr, arr + n);
long long result = 1;
for (int i = 0; i < k; i++) {
result = ((long long)arr[i] * result);
}
return result;
}
int main()
{
int arr[] = { 198, 76, 544, 123, 154, 675 };
int k = 2;
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Minimum product is " << minProduct(arr, n, k);
return 0;
}
|
Java
import java.util.Arrays;
public class Main {
public static int minProduct(int[] arr, int n, int k)
{
Arrays.sort(arr);
long result = 1;
for (int i = 0; i < k; i++) {
result = (arr[i] * result);
}
return (int)result;
}
public static void main(String[] args)
{
int[] arr = { 198, 76, 544, 123, 154, 675 };
int k = 2;
int n = arr.length;
System.out.println("Minimum product is "
+ minProduct(arr, n, k));
}
}
|
Python
def minProduct(arr, n, k):
arr.sort()
result = 1
for i in range(k):
result = (arr[i] * result)
return result
arr = [198, 76, 544, 123, 154, 675]
k = 2
n = len(arr)
print("Minimum product is", minProduct(arr, n, k))
|
C#
using System;
using System.Collections.Generic;
public class GFG
{
public static long minProduct(int[] arr, int n, int k)
{
Array.Sort(arr);
long result = 1;
for(int i = 0; i<k; i++){
result = ((long)arr[i] * result);
}
return result;
}
public static void Main(String[] args)
{
int []arr = {198, 76, 544, 123, 154, 675};
int k = 2;
int n = arr.Length;
Console.Write("Minimum product is " + minProduct(arr, n, k));
}
}
|
Javascript
function minProduct(arr, n, k) {
arr.sort((a, b) => a - b);
let result = 1;
for (let i = 0; i < k; i++) {
result = (arr[i] * result);
}
return result;
}
let arr = [198, 76, 544, 123, 154, 675];
let k = 2;
let n = arr.length;
console.log(`Minimum product is ${minProduct(arr, n, k)}`);
|
Output
Minimum product is 9348
Time Complexity: O(n*log(n))
Auxiliary Space: O(1)
An approach using Heap data structure: The idea is simple, we find the smallest k elements and print multiplication of them. In the below implementation, we have used a simple Heap-based approach where we insert array elements into a min-heap and then find product of top k elements.
Flowchart:
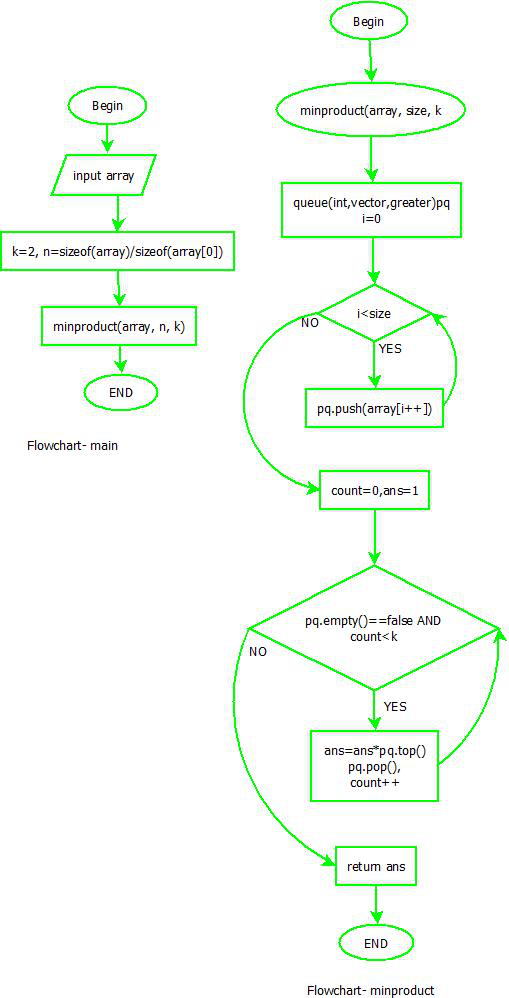
Flowchart
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int minProduct(int arr[], int n, int k)
{
priority_queue<int, vector<int>, greater<int> > pq;
for (int i = 0; i < n; i++)
pq.push(arr[i]);
int count = 0, ans = 1;
while (pq.empty() == false && count < k) {
ans = ans * pq.top();
pq.pop();
count++;
}
return ans;
}
int main()
{
int arr[] = { 198, 76, 544, 123, 154, 675 };
int k = 2;
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Minimum product is " << minProduct(arr, n, k);
return 0;
}
|
Java
import java.util.PriorityQueue;
class GFG
{
public static int minProduct(int[] arr, int n, int k)
{
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int i = 0; i < n; i++)
pq.add(arr[i]);
int count = 0;
long ans = 1;
while(pq.isEmpty() == false && count < k)
{
ans = ans * pq.element()%1000000007;
pq.remove();
count++;
}
return (int)ans;
}
public static void main(String[] args)
{
int arr[] = {198, 76, 544, 123, 154, 675};
int k = 2;
int n = arr.length;
System.out.print("Minimum product is " +
minProduct(arr, n, k));
}
}
|
Python3
import math
import heapq
def minProduct(arr, n, k):
heapq.heapify(arr)
count = 0
ans = 1
while ( arr ) and count < k:
x = heapq.heappop(arr)
ans = ans * x
count = count + 1
return ans;
arr = [198, 76, 544, 123, 154, 675]
k = 2
n = len(arr)
print ("Minimum product is",
minProduct(arr, n, k))
|
C#
using System;
using System.Collections.Generic;
public class GFG
{
public static int minProduct(int[] arr, int n, int k)
{
List<int> pq = new List<int>();
for (int i = 0; i < n; i++)
pq.Add(arr[i]);
int count = 0, ans = 1;
while(pq.Count!=0 && count < k)
{
pq.Sort();
ans = ans * pq[0];
pq.RemoveAt(0);
count++;
}
return ans;
}
public static void Main(String[] args)
{
int []arr = {198, 76, 544, 123, 154, 675};
int k = 2;
int n = arr.Length;
Console.Write("Minimum product is " +
minProduct(arr, n, k));
}
}
|
Javascript
<script>
function minProduct(arr, n, k) {
let pq = new Array();
for (let i = 0; i < n; i++)
pq.push(arr[i]);
let count = 0, ans = 1;
while (pq.length != 0 && count < k) {
pq.sort((a, b) => a - b);
ans = ans * pq[0];
pq.shift(0);
count++;
}
return ans;
}
let arr = [198, 76, 544, 123, 154, 675];
let k = 2;
let n = arr.length;
document.write("Minimum product is " + minProduct(arr, n, k));
</script>
|
Output
Minimum product is 9348
Time Complexity: O(n * log n),
Auxiliary Space: O(n) for priority queue
Note: The above problem can be solved in O(n) time using methods discussed here and here.
Share your thoughts in the comments
Please Login to comment...