Minimum number of integers required such that each Segment contains at least one of them
Last Updated :
14 Apr, 2023
Given two arrays start[] and end[] consisting of positive integers denoting the starting and ending points of a segment respectively, the task is to find the minimum number of integers which lies in at least one of the given segments and each segment contains at least one of them.
Examples:
Input: start[] = {1, 2, 3}, end[] = { 3, 5, 6}
Output: 3
Explanation:
All three ranges ([1, 3], [2, 5], [3, 6]) contains the integer 3.
Input: start[] = {4, 1, 2, 5}, end[] = {7, 3, 5, 6}
Output: 3 6
Explanation:
Segments {1, 3} and {2, 5} are contains the integer 3.
Segments {4, 7} and {5, 6} contains the integer 6.
Mathematical formulation:
The mathematical way of describing the problem is to consider each given range of integers to be a line segment defined by two integer coordinates [ai, bi] on a line. Then the minimum number of integers required to cover each of the given range is the minimum number of points such that each segment contains at least one point.
The representation of Example 1 is shown below:
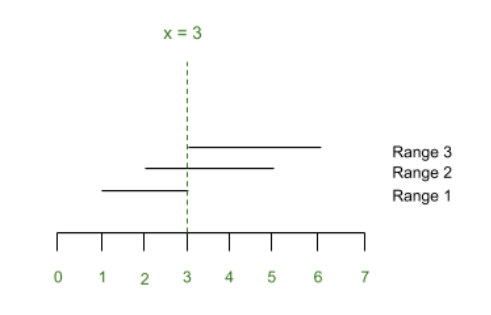
Naive approach:
The simplest way to solve the problem is to find the least value of all the starting points and maximum value of all ending points of all segments. Iterate over this range, and for each point in this range keep track of the number of segments which can be covered using this point. Use an array to store the number of segments as:
arr[point] = number of segments that can be covered using this point
- Find the maximum value in the array arr[].
- If this maximum value is equal to N, the index corresponding to this value is the point which covers all segments.
- If this maximum value is less than N, then the index corresponding to this value is a point which covers some segments.
- Repeat the steps 1 to 3 for array arr[] excluding this maximum value until the sum of all the maximum values found is equal to N.
Time Complexity: O((A-B+1)*N), where A is maximum of ending points of segments and B is the minimum of the starting points of the segments.
Auxiliary Space: O(1)
Efficient Approach:
Approach 1:
The problem can be solved efficiently by using the Greedy Technique. Follow the steps given below to solve the problem:
- Sort the segments by their end points.
- Select the point(or coordinate) corresponding to minimum end point of all segments.
- Now, All the segments whose starting point are less than this selected point and whose ending points are greater than this selected point can be covered by this point.
- Then print the minimum number of points.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool sortcol(const pair<int, int> p1,
const pair<int, int> p2)
{
return p1.second < p2.second;
}
void minPoints(pair<int, int> points[], int n)
{
sort(points, points + n, sortcol);
vector<int> coordinates;
int i = 0;
while (i < n)
{
int seg = points[i].second;
coordinates.push_back(seg);
int p = i + 1;
if (p >= n)
break;
int arrived = points[p].first;
while (seg >= arrived)
{
p += 1;
if (p >= n)
break;
arrived = points[p].first;
}
i = p;
}
for(auto point : coordinates)
cout << point << " ";
}
int main()
{
int n = 4;
int start[] = { 4, 1, 2, 5 };
int end[] = { 7, 3, 5, 6 };
pair<int, int> points[n];
for(int i = 0; i < n; i++)
{
points[i] = { start[i], end[i] };
}
minPoints(points, n);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void minPoints(int[][] points, int n)
{
Arrays.sort(points, (a, b) -> a[1] - b[1]);
ArrayList<Integer> coordinates = new ArrayList<>();
int i = 0;
while (i < n)
{
int seg = points[i][1];
coordinates.add(seg);
int p = i + 1;
if (p >= n)
break;
int arrived = points[p][0];
while (seg >= arrived)
{
p += 1;
if (p >= n)
break;
arrived = points[p][0];
}
i = p;
}
for(Integer point : coordinates)
System.out.print(point + " ");
}
public static void main(String[] args)
{
int n = 4;
int[] start = { 4, 1, 2, 5 };
int[] end = { 7, 3, 5, 6 };
int[][] points = new int[n][2];
for(int i = 0; i < n; i++)
{
points[i][0] = start[i];
points[i][1] = end[i];
}
minPoints(points, n);
}
}
|
Python3
def minPoints(points):
points.sort(key = lambda x: x[1])
coordinates = []
i = 0
while i < n:
seg = points[i][1]
coordinates.append(seg)
p = i + 1
if p >= n:
break
arrived = points[p][0]
while seg >= arrived:
p += 1
if p >= n:
break
arrived = points[p][0]
i = p
for point in coordinates:
print(point, end =" ")
n = 4
start = [4, 1, 2, 5]
end = [7, 3, 5, 6]
points = []
for i in range(n):
tu = (start[i], end[i])
points.append(tu)
minPoints(points)
|
C#
using System;
using System.Linq;
using System.Collections.Generic;
class GFG{
static void minPoints(List<int []> points, int n)
{
points = points.OrderBy(p => p[1]).ToList();
List<int> coordinates = new List<int>();
int i = 0;
while (i < n)
{
int seg = points[i][1];
coordinates.Add(seg);
int p = i + 1;
if (p >= n)
break;
int arrived = points[p][0];
while (seg >= arrived)
{
p += 1;
if (p >= n)
break;
arrived = points[p][0];
}
i = p;
}
foreach (int point in coordinates)
Console.Write(point + " ");
}
public static void Main(string[] args)
{
int n = 4;
int[] start = { 4, 1, 2, 5 };
int[] end = { 7, 3, 5, 6 };
List<int []> points = new List<int []>();
for(int i = 0; i < n; i++)
{
points.Add( new [] {start[i], end[i]});
}
minPoints(points, n);
}
}
|
Javascript
<script>
function minPoints(points){
points.sort((a,b)=>a[1]-b[1])
let coordinates = []
let i = 0
while(i < n){
let seg = points[i][1]
coordinates.push(seg)
let p = i + 1
if(p >= n)
break
let arrived = points[p][0]
while(seg >= arrived){
p += 1
if(p >= n)
break
arrived = points[p][0]
}
i = p
}
for(let point of coordinates)
document.write(point," ")
}
let n = 4
let start = [4, 1, 2, 5]
let end = [7, 3, 5, 6]
let points = []
for(let i = 0; i < n; i++){
let tu = [start[i], end[i]]
points.push(tu)
}
minPoints(points)
</script>
|
Time Complexity: O(N*log N)
Auxiliary Space: O(N)
Another approach to solve the problem of finding the minimum number of points needed to cover a set of intervals, which uses a divide and conquer algorithm.
- The idea behind the divide and conquer algorithm is to recursively divide the intervals into two halves and find the minimum number of points needed to cover each half.
- Then, we can combine the solutions for the two halves by using a point to cover the intervals that overlap.
Follow the Below steps to solve the above approach:
- If there is only one interval, return 1.
- Divide the intervals into two halves.
- Recursively find the minimum number of points needed to cover the left and right halves.
- Initialize the minimum number of points to cover the overlapping intervals to the maximum of the two halves.
- Iterate through the left and right halves.
- If the intervals overlap, update the minimum number of points to cover the overlapping intervals.
- Return the minimum number of points to cover the overlapping intervals.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minimumPoints(vector<pair<int, int> > intervals)
{
sort(intervals.begin(), intervals.end(),
[](pair<int, int> a, pair<int, int> b) {
return a.second < b.second;
});
vector<int> points;
points.push_back(intervals[0].second);
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i].first > points.back()) {
points.push_back(intervals[i].second);
}
}
return points.size();
}
int main()
{
vector<pair<int, int> > intervals
= { { 1, 3 }, { 2, 4 }, { 3, 5 }, { 6, 8 } };
cout << minimumPoints(intervals) << endl;
intervals = { { 1, 2 }, { 3, 4 }, { 2, 5 }, { 5, 8 } };
cout << minimumPoints(intervals) << endl;
}
|
Java
import java.util.Arrays;
import java.util.Comparator;
public class GFG {
public static int minimumPoints(int[][] intervals)
{
Arrays.sort(intervals, new Comparator<int[]>() {
public int compare(int[] a, int[] b)
{
return a[1] - b[1];
}
});
int[] points = new int[intervals.length];
int index = 0;
points[index] = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] > points[index]) {
points[++index] = intervals[i][1];
}
}
return index + 1;
}
public static void main(String[] args)
{
int[][] intervals
= { { 1, 3 }, { 2, 4 }, { 3, 5 }, { 6, 8 } };
System.out.println(
minimumPoints(intervals));
int[][] intervals1
= { { 1, 2 }, { 3, 4 }, { 2, 5 }, { 5, 8 } };
System.out.println(
minimumPoints(intervals1));
}
}
|
Python3
from typing import List, Tuple
def minimumPoints(intervals: List[Tuple[int, int]]) -> int:
intervals.sort(key=lambda x: x[1])
points = [intervals[0][1]]
for i in range(1, len(intervals)):
if intervals[i][0] > points[-1]:
points.append(intervals[i][1])
return len(points)
if __name__ == "__main__":
intervals = [(1, 3), (2, 4), (3, 5), (6, 8)]
minPoints = minimumPoints(intervals)
print(minPoints)
intervals = [(1, 2), (3, 4), (2, 5), (5, 8)]
minPoints = minimumPoints(intervals)
print(minPoints)
|
C#
using System;
using System.Collections.Generic;
using System.Linq;
class GFG {
public static int MinimumPoints(int[][] intervals)
{
Array.Sort(intervals,
new Comparison<int[]>(
(a, b) => a[1].CompareTo(b[1])));
int[] points = new int[intervals.Length];
int index = 0;
points[index] = intervals[0][1];
for (int i = 1; i < intervals.Length; i++) {
if (intervals[i][0] > points[index]) {
points[++index] = intervals[i][1];
}
}
return index + 1;
}
public static void Main(string[] args)
{
int[][] intervals
= { new[] { 1, 3 }, new[] { 2, 4 },
new[] { 3, 5 }, new[] { 6, 8 } };
Console.WriteLine(
MinimumPoints(intervals));
int[][] intervals1
= { new[] { 1, 2 }, new[] { 3, 4 },
new[] { 2, 5 }, new[] { 5, 8 } };
Console.WriteLine(
MinimumPoints(intervals1));
}
}
|
Javascript
function minimumPoints(intervals) {
intervals.sort((a, b) => a[1] - b[1]);
const points = [intervals[0][1]];
for (let i = 1; i < intervals.length; i++) {
if (intervals[i][0] > points[points.length - 1]) {
points.push(intervals[i][1]);
}
}
return points.length;
}
let intervals = [[1, 3], [2, 4], [3, 5], [6, 8]];
console.log(minimumPoints(intervals));
intervals = [[1, 2], [3, 4], [2, 5], [5, 8]]
console.log(minimumPoints(intervals));
|
Complexity Analysis:
Time complexity: O(N*logN), due to the recursive nature of the algorithm, where N is the number of intervals.
Auxiliary Space: O(N), since we need to store the intervals in each recursive call.
Another approach to solve the problem of finding the minimum number of integers required such that each Segment contains at least one of them, which uses a dynamic programming algorithm.
- The idea behind the dynamic programming algorithm is to iterate through the intervals and, for each interval, compute the minimum number of integers required such that each Segment contains at least one of them.
- To do this, we can use a two-dimensional array, where the first dimension represents the index of the interval and the second dimension represents the number of points.
At each step, we have two options: We can either use a new point to cover the current interval, or we can use one of the points that we have already used to cover a previous interval. If we use a new point, we need to increment the number of points by 1. If we use an existing point, we do not need to increment the number of points.
- We can compute the minimum number of points needed to cover the intervals using the following recurrence:
- dp[i][j] = min(dp[i-1][j], dp[i-1][j-1] + 1)
- The base case is when i is equal to 0, in which case dp[i][j] is equal to j.
- Using this recurrence, we can compute the minimum number of points needed to cover the intervals in O(nk) time, where n is the number of intervals and k is the maximum number of points needed to cover the intervals.
Follow the Below steps to solve the above approach:
- Sort the intervals by their starting point.
- Initialize a list minPoints with the length of the intervals, and set all elements to 1.
- Iterate through the intervals from the second to the last.
- For each interval, iterate through the minPoints list from the first element to the current interval.
- If the ending point of the previous interval is greater than or equal to the starting point of the current interval, update the current element of minPoints as the minimum of itself and the previous element plus 1.
- Return the last element of minPoints.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minimumPoints(vector<pair<int, int> > intervals)
{
sort(intervals.begin(), intervals.end());
int n = intervals.size();
vector<int> minPoints(n, 1);
for (int i = 1; i < n; i++)
for (int j = 0; j < i; j++) {
if (intervals[j].second <= intervals[i].first)
minPoints[i]
= max(minPoints[i], minPoints[j] + 1);
else
minPoints[i] = 1;
}
return minPoints[n - 1];
}
int main()
{
vector<pair<int, int> > intervals
= { { 1, 3 }, { 2, 4 }, { 3, 5 }, { 6, 8 } };
cout << minimumPoints(intervals) << endl;
intervals = { { 1, 2 }, { 3, 4 }, { 2, 5 }, { 5, 8 } };
cout << minimumPoints(intervals) << endl;
}
|
Java
import java.util.Arrays;
import java.util.Comparator;
public class GFG {
public static int minimumPoints(int[][] intervals)
{
Arrays.sort(intervals, new Comparator<int[]>() {
public int compare(int[] a, int[] b)
{
return a[0] - b[0];
}
});
int n = intervals.length;
int[] minPoints = new int[n];
Arrays.fill(minPoints, 1);
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (intervals[j][1] <= intervals[i][0])
minPoints[i] = Math.max(
minPoints[i], minPoints[j] + 1);
else
minPoints[i] = 1;
}
}
return minPoints[n - 1];
}
public static void main(String[] args)
{
int[][] intervals
= { { 1, 3 }, { 2, 4 }, { 3, 5 }, { 6, 8 } };
System.out.println(
minimumPoints(intervals));
int[][] intervals1
= { { 1, 2 }, { 3, 4 }, { 2, 5 }, { 5, 8 } };
System.out.println(
minimumPoints(intervals1));
}
}
|
Python3
from typing import List, Tuple
def minimumPoints(intervals: List[Tuple[int, int]]) -> int:
intervals.sort(key=lambda x: x[0])
n = len(intervals)
minPoints = [1] * n
for i in range(1, n):
for j in range(i):
if intervals[j][1] <= intervals[i][0]:
minPoints[i] = max(minPoints[i], minPoints[j] + 1)
else:
minPoints[i] = 1
return minPoints[-1]
if __name__ == "__main__":
intervals = [(1, 3), (2, 4), (3, 5), (6, 8)]
minPoints = minimumPoints(intervals)
print(minPoints)
intervals = [(1, 2), (3, 4), (2, 5), (5, 8)]
minPoints = minimumPoints(intervals)
print(minPoints)
|
C#
using System;
using System.Collections.Generic;
using System.Linq;
class GFG {
static int
MinimumPoints(List<Tuple<int, int> > intervals)
{
intervals
= intervals.OrderBy(t => t.Item1).ToList();
int n = intervals.Count;
List<int> minPoints
= Enumerable.Repeat(1, n).ToList();
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (intervals[j].Item2
<= intervals[i].Item1)
minPoints[i] = Math.Max(
minPoints[i], minPoints[j] + 1);
else
minPoints[i] = 1;
}
}
return minPoints[n - 1];
}
static void Main(string[] args)
{
List<Tuple<int, int> > intervals
= new List<Tuple<int, int> >() {
Tuple.Create(1, 3), Tuple.Create(2, 4),
Tuple.Create(3, 5), Tuple.Create(6, 8)
};
Console.WriteLine(
MinimumPoints(intervals));
intervals = new List<Tuple<int, int> >() {
Tuple.Create(1, 2), Tuple.Create(3, 4),
Tuple.Create(2, 5), Tuple.Create(5, 8)
};
Console.WriteLine(
MinimumPoints(intervals));
}
}
|
Javascript
function minimumPoints(intervals)
{
intervals.sort((a, b) => a[0] - b[0]);
const n = intervals.length;
const minPoints = new Array(n).fill(1);
for (let i = 1; i < n; i++) {
for (let j = 0; j < i; j++) {
if (intervals[j][1] <= intervals[i][0]) {
minPoints[i] = Math.max(minPoints[i],
minPoints[j] + 1);
}
else {
minPoints[i] = 1;
}
}
}
return minPoints[n - 1];
}
const intervals = [
[ 1, 3 ],
[ 2, 4 ],
[ 3, 5 ],
[ 6, 8 ],
];
console.log(minimumPoints(intervals));
const intervals2 = [
[ 1, 2 ],
[ 3, 4 ],
[ 2, 5 ],
[ 5, 8 ],
];
console.log(minimumPoints(intervals2));
|
Complexity Analysis:
Time complexity: O(N2), due to the nested loops, where N is the number of intervals.
Auxiliary Space: O(N), since we need to store the minPoints list.
Share your thoughts in the comments
Please Login to comment...