Minimum number of edges required to be removed from an Undirected Graph to make it acyclic
Last Updated :
21 Jun, 2021
Given an undirected graph consisting of N nodes containing values from the range [1, N] and M edges in a matrix Edges[][], the task is to determine the minimum number of edges required to be removed such that the resulting graph does not contain any cycle.
Examples:
Input: N = 3, M = 3, edges[][] = [[1, 2], [2, 3], [3, 1]]
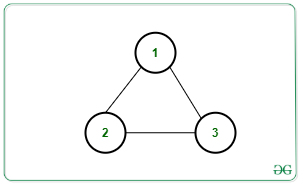
Output: 1
Explanation:
Removing any one of the edges will make the graph acyclic. Therefore, at least one edge needs to be removed.
Input: N = 3, M = 2, edges[][] = [[1, 2], [2, 3]]

Output: 0
Explanation: Graph is already acyclic. Therefore, no edge removal is required.
Naive Approach: The simplest approach is to try deleting all possible combination of sequence of edges from the given graph one by one and for each combination, count the number of removals required to make the graph acyclic. Finally, among these combinations, choose the one which deletes the minimum number of edges to obtain an acyclic graph.
Time Complexity: O(M!)
Auxiliary Space: O(N + M)
Efficient Approach: The above approach can be optimized based on the following observations:
- A graph is acyclic when it is a Tree or a forest of trees(disconnected groups of trees).
- A tree with C nodes will have (C – 1) edges.
- If there are K connected components from C1 to CK, then minimum number of edges to be removed is equal to:
M – (C1 – 1) – (C2 – 1) … (Ck -1 )
=> M – (C1 + … + CK) + K
=> M – N + K
Follow the steps below to solve the problem:
- Find the number of connected components from the given graph using DFS.
- Considering the count of connected components to be K, then print M – N + K as the required minimum number of edges to be removed to make the resulting graph acyclic.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> vec[100001];
bool vis[100001];
int cc = 1;
void dfs(int node)
{
vis[node] = true;
for (auto x : vec[node]) {
if (!vis[x]) {
cc++;
dfs(x);
}
}
}
void addEdge(int u, int v)
{
vec[u].push_back(v);
vec[v].push_back(u);
}
void minEdgeRemoved(int N, int M,
int Edges[][2])
{
for (int i = 0; i < M; i++) {
addEdge(Edges[i][0],
Edges[i][1]);
}
memset(vis, false, sizeof(vis));
int k = 0;
for (int i = 1; i <= N; i++) {
if (!vis[i]) {
cc = 1;
dfs(i);
k++;
}
}
cout << M - N + k << endl;
}
int main()
{
int N = 3, M = 2;
int Edges[][2] = { { 1, 2 }, { 2, 3 } };
minEdgeRemoved(N, M, Edges);
}
|
Java
import java.util.*;
class GFG{
@SuppressWarnings("unchecked")
static Vector<Integer> []vec = new Vector[100001];
static boolean []vis = new boolean[100001];
static int cc = 1;
static void dfs(int node)
{
vis[node] = true;
for(int x : vec[node])
{
if (!vis[x])
{
cc++;
dfs(x);
}
}
}
static void addEdge(int u, int v)
{
vec[u].add(v);
vec[v].add(u);
}
static void minEdgeRemoved(int N, int M,
int Edges[][])
{
for(int i = 0; i < M; i++)
{
addEdge(Edges[i][0],
Edges[i][1]);
}
int k = 0;
for(int i = 1; i <= N; i++)
{
if (!vis[i])
{
cc = 1;
dfs(i);
k++;
}
}
System.out.print(M - N + k + "\n");
}
public static void main(String[] args)
{
int N = 3, M = 2;
int Edges[][] = { { 1, 2 }, { 2, 3 } };
for(int i = 0; i < vec.length; i++)
vec[i] = new Vector<Integer>();
minEdgeRemoved(N, M, Edges);
}
}
|
Python3
vec = [[] for i in range(100001)]
vis = [False] * 100001
cc = 1
def dfs(node):
global cc
vis[node] = True
for x in vec[node]:
if (vis[x] == 0):
cc += 1
dfs(x)
def addEdge(u, v):
vec[u].append(v)
vec[v].append(u)
def minEdgeRemoved(N, M, Edges):
global cc
for i in range(M):
addEdge(Edges[i][0], Edges[i][1])
k = 0
for i in range(1, N + 1):
if (not vis[i]):
cc = 1
dfs(i)
k += 1
print(M - N + k)
if __name__ == '__main__':
N = 3
M = 2
Edges = [ [ 1, 2 ], [ 2, 3 ] ]
minEdgeRemoved(N, M, Edges)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static List<int> []vec = new List<int>[100001];
static bool []vis = new bool[100001];
static int cc = 1;
static void dfs(int node)
{
vis[node] = true;
foreach(int x in vec[node])
{
if (!vis[x])
{
cc++;
dfs(x);
}
}
}
static void addEdge(int u, int v)
{
vec[u].Add(v);
vec[v].Add(u);
}
static void minEdgeRemoved(int N, int M,
int [,]Edges)
{
for(int i = 0; i < M; i++)
{
addEdge(Edges[i, 0],
Edges[i, 1]);
}
int k = 0;
for(int i = 1; i <= N; i++)
{
if (!vis[i])
{
cc = 1;
dfs(i);
k++;
}
}
Console.Write(M - N + k + "\n");
}
public static void Main(String[] args)
{
int N = 3, M = 2;
int [,]Edges = { { 1, 2 }, { 2, 3 } };
for(int i = 0; i < vec.Length; i++)
vec[i] = new List<int>();
minEdgeRemoved(N, M, Edges);
}
}
|
Javascript
<script>
let vec = new Array(100001);
let vis = new Array(100001);
vis.fill(false);
let cc = 1;
function dfs(node)
{
vis[node] = true;
for(let x = 0; x < vec[node].length; x++)
{
if (!vis[vec[node][x]])
{
cc++;
dfs(vec[node][x]);
}
}
}
function addEdge(u, v)
{
vec[u].push(v);
vec[v].push(u);
}
function minEdgeRemoved(N, M, Edges)
{
for(let i = 0; i < M; i++)
{
addEdge(Edges[i][0], Edges[i][1]);
}
let k = 0;
for(let i = 1; i <= N; i++)
{
if (!vis[i])
{
cc = 1;
dfs(i);
k++;
}
}
document.write((M - N + k) + "</br>");
}
let N = 3, M = 2;
let Edges = [ [ 1, 2 ], [ 2, 3 ] ];
for(let i = 0; i < vec.length; i++)
vec[i] = [];
minEdgeRemoved(N, M, Edges);
</script>
|
Time Complexity: O(N + M)
Auxiliary Space: O(N + M)
Share your thoughts in the comments
Please Login to comment...