Minimum number of cuts required to pay salary from N length Gold Bar

Given a gold bar of length N with N equal markings, the task is to find the minimum number of cuts required to pay the salary in N days such that on any i^th day the worker has i parts of the gold bar.
Examples:

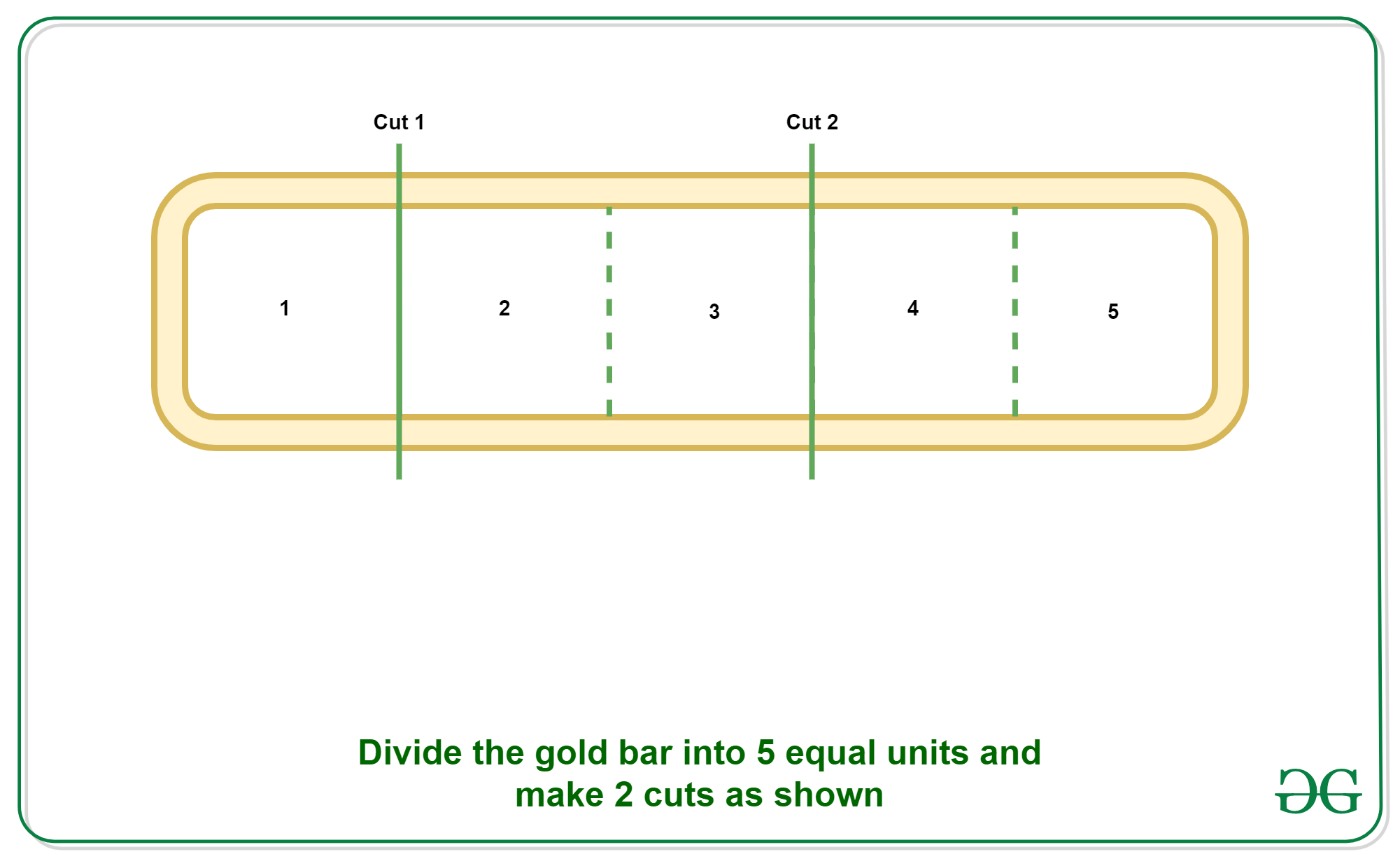
Input: N = 5 
Output: 2 
Explanation:
Divide the 5 length Gold bar into 3 part of length 1, 2, 2 by making 2 cuts. Then salary for each day will be as: 
For Day 1 = 1 (Give 1 length bar) 
For Day 2 = 2 – 1 = 1 (Give 2 length bar and take back 1 length bar) 
For Day 3 = 1 (Give 1 length bar) 
For Day 4 = 2 – 1 = 1 (Give 2 length bar and take back 1 length bar) 
For Day 5 = 1 (Give 1 length bar) 

Input: N = 15 
Output: 3 
Explanation:
Divide the 15 length Gold bar into 4 part of length 1, 2, 4, 8 by making 3 cuts. Then salary for each day will be as: 
For Day 1 = 1 (Give 1 length bar) 
For Day 2 = 2 – 1 = 1 (Give 2 length bar and take back 1 length bar) 
For Day 3 = 1 (Give 1 length bar) 
For Day 4 = 4 – 2 – 1 = 1 (Give 4 length bar and take back 1 and 2 length bar) 
For Day 5 = 1 (Give 1 length bar) 
For Day 6 = 2 – 1 = 1 (Give 2 length bar and take back 1 length bar) 
For Day 7 = 1 (Give 1 length bar) 
For Day 8 = 8 – 4 – 2 – 1 = 1 (Give 8 length bar and take back 1, 2 and 4 length bar) 
For Day 9 = 1 (Give 1 length bar) 
For Day 10 = 2 – 1 = 1 (Give 2 length bar and take back 1 length bar) 
For Day 11 = 1 (Give 1 length bar) 
For Day 12 = 4 – 2 – 1 = 1 (Give 4 length bar and take back 1 and 2 length bar) 
For Day 13 = 1 (Give 1 length bar) 
For Day 14 = 2 – 1 = 1 (Give 2 length bar and take back 1 length bar) 
For Day 15 = 1 (Give 1 length bar) 

Approach:
As we know any number can be represented with the help of the numbers in the form of powers of 2. So If we cut the length of Gold Bar into the nearest integer to log₂ (N) then we can represent any number up to N. 
For example: When N = 15, we can divide the number into the parts 1, 2, 4, 8 and using these numbers we can represent any number from 1 to 15, as shown below: 

For 1 - 1
For 2 - 2
For 3 - 2 + 1
For 4 - 4
For 5 - 4 + 1
For 6 - 4 + 2
For 7 - 4 + 2 + 1
For 8 - 8
For 9 - 8 + 1
For 10 - 8 + 2
For 11 - 8 + 2 + 1
For 12 - 8 + 4
For 13 - 8 + 4 + 1
For 14 - 8 + 4 + 2
For 15 - 8 + 4 + 2 + 1

Below is the implementation of the above approach.

C++

// CPP Implementation to find
// the minimum number of cuts to
// pay the worker.
#include <bits/stdc++.h>

using namespace std;

// Function to find the minimum
// number of cuts to pay the worker.
int pay(int n)
{

    // Nearest Integer to the Log
    // value of the number N
    int cuts = int(log(n)/log(2));

    return cuts;
}

// Driver code
int main()
{
    int n = 5;
    int cuts = pay(n);
    cout << cuts << endl;

    // Cuts Required in the
    // Length of 15
    n = 15;
    cuts = pay(n);
    cout<<(cuts);

    return 0;
}

// This code is contributed by mohit kumar 29

Java

// JAVA Implementation to find
// the minimum number of cuts to
// pay the worker.
class GFG
{

// Function to find the minimum
// number of cuts to pay the worker.
static int pay(int n)
{

    // Nearest Integer to the Log
    // value of the number N
    int cuts = (int) (Math.log(n)/Math.log(2));

    return cuts;
}

// Driver code
public static void main(String[] args)
{
    int n = 5;
    int cuts = pay(n);
    System.out.print(cuts +"\n");

    // Cuts Required in the
    // Length of 15
    n = 15;
    cuts = pay(n);
    System.out.print(cuts);
}
}

// This code is contributed by 29AjayKumar

Python

# Python Implementation to find
# the minimum number of cuts to
# pay the worker.

import math

# Function to find the minimum
# number of cuts to pay the worker.
def pay(n):

    # Nearest Integer to the Log
    # value of the number N
    cuts = int(math.log(n, 2))

    return cuts

# Driver Code
if __name__ == "__main__":
    n = 5
    cuts = pay(n)
    print(cuts)

    # Cuts Required in the
    # Length of 15
    n = 15
    cuts = pay(n)
    print(cuts)

C#

// C# Implementation to find
// the minimum number of cuts to
// pay the worker.
using System;

class GFG
{

// Function to find the minimum
// number of cuts to pay the worker.
static int pay(int n)
{

    // Nearest int to the Log
    // value of the number N
    int cuts = (int) (Math.Log(n)/Math.Log(2));

    return cuts;
}

// Driver code
public static void Main(String[] args)
{
    int n = 5;
    int cuts = pay(n);
    Console.Write(cuts +"\n");

    // Cuts Required in the
    // Length of 15
    n = 15;
    cuts = pay(n);
    Console.Write(cuts);
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>

// JavaScript Implementation to find
// the minimum number of cuts to
// pay the worker.

// Function to find the minimum
// number of cuts to pay the worker.
function pay(n)
{

    // Nearest Integer to the Log
    // value of the number N
    let cuts = parseInt(Math.log(n)/Math.log(2));

    return cuts;
}

// Driver code
    let n = 5;
    let cuts = pay(n);
    document.write(cuts + "<br>");

    // Cuts Required in the
    // Length of 15
    n = 15;
    cuts = pay(n);
    document.write(cuts + "<br>");

</script>

Output:

2
3

Time Complexity: O(1)

Auxiliary Space: O(1)