Minimum cuts required to convert a palindromic string to a different palindromic string
Last Updated :
06 Nov, 2021
Given palindromic string s, the task is to find minimum k, such that you can cut this string into k+1 parts, and then unite them in such a way that the final string will be a palindrome and it won’t be equal to the initial string s. If it is impossible then print -1.
Examples:
Input : string = "civic"
Output : 2
Explanation : ci | v | ic --> ic | v | ci --> icvci
Input : string = "gggg"
Output : -1
Input : string = "redder"
Output : 1
Explanation : red | der --> der | red --> derred
Input : string = "aaaasaaaa"
Output : -1
Approach 1: It is given that formed palindromic string should be different from the given string.
So when our string consists of n or n-1 (when n is odd) equal characters, then there is no way to get the answer. For example –
String : "aaaasaaaa"
String : "aaaa"
Above strings can not form palindrome other than the given one.
Otherwise, cut the longest prefix of s of length l, that consists of equal characters of length equal to l-1. Now similarly cut suffix of length l-1, and call remaining part as mid.
Now we have prefix = s[1..l] and suff = s[(n-l+1)..n]. Swap prefix and suffix, then unite all three parts together and keep mid as it is.
prefix + mid + suffix 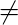 [Tex]suffix + mid + prefix[/Tex]
[Tex]suffix + mid + prefix[/Tex]
So clearly we can get the answer in two cuts. Finally you just have to check if it is possible to get answer in one cut. For that just cut one element from end and append it at front and continue this cyclic shift. During this if we get a palindromic string other then the given one then it means we can get answer in just one cut.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPalindrome(string s)
{
for (int i = 0; i < s.length(); ++i) {
if (s[i] != s[s.length() - i - 1]) {
return false;
}
}
return true;
}
bool ans(string s)
{
string s2 = s;
for (int i = 0; i < s.length(); ++i) {
s2 = s2.back() + s2;
s2.pop_back();
if (s != s2 && isPalindrome(s2)) {
return true;
}
}
return false;
}
int solve(string s)
{
if (s.length() <= 3) {
return -1;
}
int cnt[25] = {};
for (int i = 0; i < s.length(); i++) {
cnt[s[i] - 'a']++;
}
if (*max_element(cnt, cnt + 25) >= (s.length() - 1)) {
return -1;
}
else {
return (ans(s) ? 1 : 2);
}
}
int main()
{
string s = "nolon";
cout << solve(s);
return 0;
}
|
Java
import java.util.Arrays;
class GFG
{
static boolean isPalindrome(String s)
{
for (int i = 0; i < s.length(); ++i)
{
if (s.charAt(i) != s.charAt(s.length() - i - 1))
{
return false;
}
}
return true;
}
static boolean ans(String s)
{
String s2 = s;
for (int i = 0; i < s.length(); ++i)
{
s2 = s2.charAt(s2.length()-1) + s2;
s2 = s2.substring(0,s2.length()-1);
if ((s == null ? s2 != null : !s.equals(s2)) &&
isPalindrome(s2))
{
return true;
}
}
return false;
}
static int solve(String s)
{
if (s.length() <= 3)
{
return -1;
}
int cnt[] = new int[25];
for (int i = 0; i < s.length(); i++)
{
cnt[s.charAt(i) - 'a']++;
}
if (Arrays.stream(cnt).max().getAsInt() >=
(s.length() - 1))
{
return -1;
}
else
{
return (ans(s) ? 1 : 2);
}
}
public static void main(String[] args)
{
String s = "nolon";
System.out.println(solve(s));
}
}
|
Python3
def isPalindrome(s):
for i in range(len(s)):
if (s[i] != s[len(s) - i - 1]):
return False
return true
def ans(s):
s2 = s
for i in range(len(s)):
s2 = s2[len(s2) - 1] + s2
s2 = s2[0:len(s2) - 1]
if (s != s2 and isPalindrome(s2)):
return True
return False
def solve(s):
if (len(s) <= 3):
return -1
cnt = [0 for i in range(26)]
for i in range(len(s)):
cnt[ord(s[i]) - ord('a')] += 1
max = cnt[0]
for i in range(len(cnt)):
if cnt[i]>max:
max = cnt[i]
if (max >= len(s) - 1):
return -1
else:
if ans(s) == True:
return 1
else:
return 2
if __name__ == '__main__':
s = "nolon"
print(solve(s))
|
C#
using System;
using System.Linq;
class GFG
{
static bool isPalindrome(string s)
{
for (int i = 0; i < s.Length; ++i)
{
if (s[i] != s[s.Length - i - 1])
{
return false;
}
}
return true;
}
static bool ans(string s)
{
string s2 = s;
for (int i = 0; i < s.Length; ++i)
{
s2 = s2[s2.Length-1] + s2;
s2 = s2.Substring(0,s2.Length-1);
if ((s == null ? s2 != null : !s.Equals(s2)) &&
isPalindrome(s2))
{
return true;
}
}
return false;
}
static int solve(string s)
{
if (s.Length <= 3)
{
return -1;
}
int[] cnt = new int[25];
for (int i = 0; i < s.Length; i++)
{
cnt[s[i] - 'a']++;
}
if (cnt.Max() >=(s.Length - 1))
{
return -1;
}
else
{
return (ans(s) ? 1 : 2);
}
}
static void Main()
{
string s = "nolon";
Console.WriteLine(solve(s));
}
}
|
Javascript
<script>
function isPalindrome(s)
{
for (let i = 0; i < s.length; ++i)
{
if (s[i] != s[s.length - i - 1])
{
return false;
}
}
return true;
}
function ans(s)
{
let s2 = s;
for (let i = 0; i < s.length; ++i)
{
s2 = s2[s2.length-1] + s2;
s2 = s2.substring(0,s2.length-1);
if ((s == null ? s2 != null : !s == (s2)) &&
isPalindrome(s2))
{
return true;
}
}
return false;
}
function solve(s)
{
if (s.length <= 3)
{
return -1;
}
let cnt = new Array(25);
for(let i=0;i<25;i++)
cnt[i]=0;
for (let i = 0; i < s.length; i++)
{
cnt[s[i].charCodeAt(0) - 'a'.charCodeAt(0)]++;
}
if (Math.max(...cnt) >= (s.length - 1))
{
return -1;
}
else
{
return (ans(s) ? 1 : 2);
}
}
let s = "nolon";
document.write(solve(s));
</script>
|
Time Complexity: O(N2)
Auxiliary Space: O(N)
Efficient Approach: Again if our string consists of n or n-1 (when n is odd) equal characters, then there is no way to get the answer.
Now, divide this problem into two parts that whether the string length is even or odd.
If the string length is odd then we always have a middle element in it so just make 2 cuts around the middle element and split the string into three segments and swap first and third segments.
Say, we have a string:
nolon --> no | l | on --> on | l | no --> onlno
If the string length is even then check whether the half string is itself a palindromic string or not.
If so then:
- Split a string recursively into two parts and check whether the resulting half string is a palindrome or not.
- If string became of odd length then simply return 2.
asaasa --> as | aa | sa --> sa | aa | as --> saaaas
- If resulting string is not a palindrome then return 1.
toottoot --> to | ottoot --> ottoot | to --> ottootto
Else we can cut this string from the middle, form two segments and swap each other.
For Example:
voov --> vo | ov --> ov | vo --> ovvo
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int solveEven(string s)
{
if (s.length() % 2 == 1)
return 2;
string ls = s.substr(0, s.length() / 2);
string rs = s.substr(s.length() / 2, s.length());
if (ls != rs)
return 1;
return solveEven(ls);
}
int solveOdd(string s)
{
return 2;
}
int solve(string s)
{
if (s.length() <= 3) {
return -1;
}
int cnt[25] = {};
for (int i = 0; i < s.length(); i++) {
cnt[s[i] - 'a']++;
}
if (*max_element(cnt, cnt + 25) >= s.length() - 1) {
return -1;
}
if (s.length() % 2 == 0)
return solveEven(s);
if (s.length() % 2 == 1)
return solveOdd(s);
}
int main()
{
string s = "nolon";
cout << solve(s);
return 0;
}
|
Java
import java.util.Arrays;
class GFG
{
static int solveEven(String s)
{
if (s.length() % 2 == 1)
{
return 2;
}
String ls = s.substring(0, s.length() / 2);
String rs = s.substring(s.length() / 2, s.length());
if (ls != rs)
{
return 1;
}
return solveEven(ls);
}
static int solveOdd(String s)
{
return 2;
}
static int solve(String s)
{
if (s.length() <= 3)
{
return -1;
}
int cnt[] = new int[25];
for (int i = 0; i < s.length(); i++)
{
cnt[s.charAt(i) - 'a']++;
}
if (Arrays.stream(cnt).max().getAsInt() >= s.length() - 1)
{
return -1;
}
if (s.length() % 2 == 0)
{
return solveEven(s);
}
if (s.length() % 2 == 1)
{
return solveOdd(s);
}
return Integer.MIN_VALUE;
}
public static void main(String[] args)
{
String s = "nolon";
System.out.println(solve(s));
}
}
|
Python3
def solveEven(s):
if len(s) % 2 == 1:
return 2
ls = s[0 : len(s) // 2]
rs = s[len(s) // 2 : len(s)]
if ls != rs:
return 1
return solveEven(ls)
def solveOdd(s):
return 2
def solve(s):
if len(s) <= 3:
return -1
cnt = [0] * 25
for i in range(0, len(s)):
cnt[ord(s[i]) - ord('a')] += 1
if max(cnt) >= len(s) - 1:
return -1
if len(s) % 2 == 0:
return solveEven(s)
if len(s) % 2 == 1:
return solveOdd(s)
if __name__ == "__main__":
s = "nolon"
print(solve(s))
|
C#
using System;
using System.Linq;
class GFG
{
static int solveEven(String s)
{
if (s.Length % 2 == 1)
{
return 2;
}
String ls = s.Substring(0, s.Length / 2);
String rs = s.Substring(s.Length / 2, s.Length);
if (ls != rs)
{
return 1;
}
return solveEven(ls);
}
static int solveOdd(String s)
{
return 2;
}
static int solve(String s)
{
if (s.Length <= 3)
{
return -1;
}
int []cnt = new int[25];
for (int i = 0; i < s.Length; i++)
{
cnt[s[i] - 'a']++;
}
if (cnt.Max() >= s.Length - 1)
{
return -1;
}
if (s.Length % 2 == 0)
{
return solveEven(s);
}
if (s.Length % 2 == 1)
{
return solveOdd(s);
}
return int.MinValue;
}
public static void Main()
{
String s = "nolon";
Console.WriteLine(solve(s));
}
}
|
Javascript
<script>
function solveEven(s)
{
if (s.length % 2 == 1)
{
return 2;
}
let ls = s.substring(0, s.length / 2);
let rs = s.substring(s.length / 2, s.length);
if (ls != rs)
{
return 1;
}
return solveEven(ls);
}
function solveOdd(s)
{
return 2;
}
function solve(s)
{
if (s.length <= 3)
{
return -1;
}
let cnt = new Array(25);
for(let i=0;i<25;i++)
cnt[i]=0;
for (let i = 0; i < s.length; i++)
{
cnt[s[i].charCodeAt(0) - 'a'.charCodeAt(0)]++;
}
if (Math.max(...cnt) >= s.length - 1)
{
return -1;
}
if (s.length % 2 == 0)
{
return solveEven(s);
}
if (s.length % 2 == 1)
{
return solveOdd(s);
}
return Number.MIN_VALUE;
}
let s = "nolon";
document.write(solve(s));
</script>
|
Time Complexity : O(N)
Auxiliary Space: O(max(26,N))
Share your thoughts in the comments
Please Login to comment...