Minimum increments or decrements required to convert a sorted array into a power sequence

Given a sorted array arr[] consisting of N positive integers, the task is to minimize the total number of increments or decrements of each array element required to convert the given array into a power sequence of any arbitrary integer X.

A sequence is called a power sequence of any integer X, if and only if for every i^th element (0 ≤ i < N), arr[i] = Xⁱ, where N is length of the given array.

Examples:

Input: arr[] = {1, 3, 4}
Output: 1
Explanation: Decreasing arr[1] by 1 modifies array to {1, 2, 4}, which is a power sequence of 2. Therefore, the total number of increments or decrements required is 1.

Input: arr[] = {1, 5, 7}
Output: 6
Explanation:
Operation 1: Decreasing arr[1] by 1 modifies array to {1, 4, 7}
Operation 2: Decreasing arr[1] by 1 modifies array to {1, 3, 7}
Operation 3: Increasing arr[2] by 1 modifies array to {1, 3, 8}
Operation 4: Increasing arr[2] by 1 modifies array to {1, 3, 9}, which is the power sequence of 3. Therefore, the total number of increments or decrements required is 4.

Approach: The given problem can be solved based on the following observations:

• As the given array needs to be converted into a power sequence for any arbitrary integer X, then the mathematical relations can be written as:

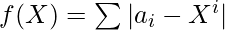
where, 0 <= i < N, N is the number of elements in the array.

• The minimum value of f(X) is the minimum number of operations required to convert it into a power sequence of X and the maximum value of X can be calculated as follows:

=> 
=>

• Therefore, the idea is to iterate for all possible values of X starting from 1, and check if the following equation satisfies or not: 
  
  If found to be true, then find all possible values of 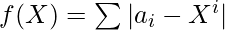and return the minimum among all the values obtained.

Follow the steps below to solve the given problem:

• Initialize a variable, say ans as (the sum of array elements – N), that stores the minimum number of increments or decrements required to make the array a power sequence.
• Iterate a loop, starting from 1, using the variable X and perform the following steps: 
  • Initialize two variables, say currCost as 0 and currPower as 1, that stores the sum of the expression 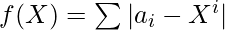and power of the integer X.
  • Iterate over the range [0, N – 1] and update the value of currCost as currCost + abs(arr[i] – currPower) and the value of currPower as X * currPower.
  • If the expression is not satisfied, then break out of the loop. Otherwise, update the value of ans to the minimum of ans and currCost.
• After completing the above steps, print the value of ans as the required minimum number of operations.

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to find the minimum number
// of increments or decrements required
// to convert array into a power sequence
int minOperations(int a[], int n)
{
    // Initialize the count to f(X) for X = 1
    int ans = accumulate(a, a + n, 0) - n;

    // Calculate the value of f(X)
    // X ^ (n - 1) <= f(1) + a[n - 1]
    for (int x = 1;; x++) {

        int curPow = 1, curCost = 0;

        // Calculate F(x)
        for (int i = 0; i < n; i++) {
            curCost += abs(a[i] - curPow);
            curPow *= x;
        }

        // Check if X ^ (n - 1) > f(1) + a[n - 1]
        if (curPow / x > ans + a[n - 1])
            break;

        // Update ans to store the
        // minimum of ans and F(x)
        ans = min(ans, curCost);
    }

    // Return the minimum number
    // of operations required
    return ans;
}

// Driver Code
int main()
{
    int arr[] = { 1, 5, 7 };
    int N = sizeof(arr) / sizeof(arr[0]);

    cout << minOperations(arr, N);

    return 0;
}

Java

// Java program for the above approach
class GFG{

// Function to find the minimum number
// of increments or decrements required
// to convert array into a power sequence
static int minOperations(int a[], int n)
{

    // Initialize the count to f(X) for X = 1
    int ans = 0;
    for(int i = 0; i < n; i++)
    {
        ans += a[i];
    }
    ans -= n;

    // Calculate the value of f(X)
    // X ^ (n - 1) <= f(1) + a[n - 1]
    for(int x = 1;; x++)
    {
        int curPow = 1, curCost = 0;

        // Calculate F(x)
        for(int i = 0; i < n; i++)
        {
            curCost += Math.abs(a[i] - curPow);
            curPow *= x;
        }

        // Check if X ^ (n - 1) > f(1) + a[n - 1]
        if (curPow / x > ans + a[n - 1])
            break;

        // Update ans to store the
        // minimum of ans and F(x)
        ans = Math.min(ans, curCost);
    }

    // Return the minimum number
    // of operations required
    return ans;
}

// Driver Code
public static void main(String[] args)
{
    int arr[] = { 1, 5, 7 };
    int N = arr.length;

    System.out.print(minOperations(arr, N));
}
}

// This code is contributed by avijitmondal1998

Python3

# Python3 program for the above approach

# Function to find the minimum number
# of increments or decrements required
# to convert array into a power sequence
def minOperations(a, n):

    # Initialize the count to f(X) for X = 1
    ans = 0
    for i in range(n):
        ans += a[i]

    ans -= n

    # Calculate the value of f(X)
    # X ^ (n - 1) <= f(1) + a[n - 1]
    x = 1
    while(1):
        curPow = 1
        curCost = 0

        # Calculate F(x)
        for i in range(n):
            curCost += abs(a[i] - curPow)
            curPow *= x

        # Check if X ^ (n - 1) > f(1) + a[n - 1]
        if (curPow / x > ans + a[n - 1]):
            break

        # Update ans to store the
        # minimum of ans and F(x)
        ans = min(ans, curCost)
        x += 1

    # Return the minimum number
    # of operations required
    return ans

# Driver Code
if __name__ == '__main__':

    arr =  [1, 5, 7]
    N = len(arr)

    print(minOperations(arr, N))

# This code is contributed by ipg2016107

C#

// C# program for the above approach
using System;

class GFG{

// Function to find the minimum number
// of increments or decrements required
// to convert array into a power sequence
static int minOperations(int []a, int n)
{

    // Initialize the count to f(X) for X = 1
    int ans = 0;
    for(int i = 0; i < n; i++)
    {
        ans += a[i];
    }
    ans -= n;

    // Calculate the value of f(X)
    // X ^ (n - 1) <= f(1) + a[n - 1]
    for(int x = 1;; x++)
    {
        int curPow = 1, curCost = 0;

        // Calculate F(x)
        for(int i = 0; i < n; i++)
        {
            curCost += Math.Abs(a[i] - curPow);
            curPow *= x;
        }

        // Check if X ^ (n - 1) > f(1) + a[n - 1]
        if (curPow / x > ans + a[n - 1])
            break;

        // Update ans to store the
        // minimum of ans and F(x)
        ans = Math.Min(ans, curCost);
    }

    // Return the minimum number
    // of operations required
    return ans;
}

// Driver Code
public static void Main()
{
    int []arr = { 1, 5, 7 };
    int N = arr.Length;

    Console.WriteLine(minOperations(arr, N));
}
}

// This code is contributed by mohit kumar 29

Javascript

<script>

// JavaScript program for the above approach

// Function to find the minimum number
// of increments or decrements required
// to convert array into a power sequence
    function minOperations(a , n) {

        // Initialize the count to f(X) for X = 1
        var ans = 0;
        for (i = 0; i < n; i++) {
            ans += a[i];
        }
        ans -= n;

        // Calculate the value of f(X)
        // X ^ (n - 1) <= f(1) + a[n - 1]
        for (x = 1;; x++) {
            var curPow = 1, curCost = 0;

            // Calculate F(x)
            for (i = 0; i < n; i++) {
                curCost += Math.abs(a[i] - curPow);
                curPow *= x;
            }

            // Check if X ^ (n - 1) > f(1) + a[n - 1]
            if (curPow / x > ans + a[n - 1])
                break;

            // Update ans to store the
            // minimum of ans and F(x)
            ans = Math.min(ans, curCost);
        }

        // Return the minimum number
        // of operations required
        return ans;
    }

    // Driver Code

        var arr = [ 1, 5, 7 ];
        var N = arr.length;

        document.write(minOperations(arr, N));

// This code contributed by aashish1995

</script>

Output:

4

Time Complexity: O(N*(S)^{(1/(N – 1))})
Auxiliary Space: O(1)