Minimize number of cuts required to break N length stick into N unit length sticks
Last Updated :
31 Mar, 2021
Given an integer N denoting the length of a given stick, the task is to minimize the time required to split the stick into pieces of unit length, given that, a single cut is possible for any portion of stick at any instance of time.
Examples:
Input: N = 100
Output: 7
Explanation:
(100 units) —> (2 portions of 50 units) —> (4 portions of 25 units) —> (4 portions of 12 units, 4 portions of 13 units) —> (12 portions of 6 units, 4 portions of 7 units) —> (28 portions of 3 units, 4 portions of 4 units) —> (28 portions of 1 unit, 36 portions of 2 units) —> (100 portions of 1 unit)
Input: N = 65
Output: 7
Explanation:
(65 units) —> (1 portion of 32 units, 1 portion of 33 units) —> (3 portions of 16 units, 1 portion of 17 units) —> (7 portions of 8 units, 1 portions of 9 units) —> (15 portions of 4 units, 1 portion of 5 units) —> (31 portions of 2 units, 1 portions of 3 units) —> (63 portions of 1 unit, 1 portion of 2 units) —> (65 portions of 1 unit)
Approach:
Since we can cut any portion of the stick once at a particular instance of time, we need to maximize the portions after every cut. So, we will cut the stick into two parts of the longest possible length with the first cut. In the next instance, further cut both the obtained parts into two longest parts each in the next cut. Repeat this until N unit pieces are obtained.
Illustration:
N = 100
1st Cut: (50) + (50)
2nd Cut: (25) + (25) + (25) + (25)
3rd Cut: (12) + (13) + (12) + (13) + (12) + (13) + (12) + (13)
4th Cut: (6) + (6) + (6) + (7) + (6) + (6) + (6) + (7) + (6) + (6) + (6) + (7) + (6) + (6) + (6) + (7)
5th Cut: (3) + (3) + (3) + (3) + (3) + (3) + (3) + (4) + (3) + (3) + (3) + (3) + (3) + (3) + (3) + (4) + (3) + (3) + (3) + (3) + (3) + (3) + (3) + (4) + (3) + (3) + (3) + (3) + (3) + (3) + (3) + (4)
6th Cut: 28 portions of 1 unit, 36 portions of 2 units
7th Cut: 100 portions of 1 unit
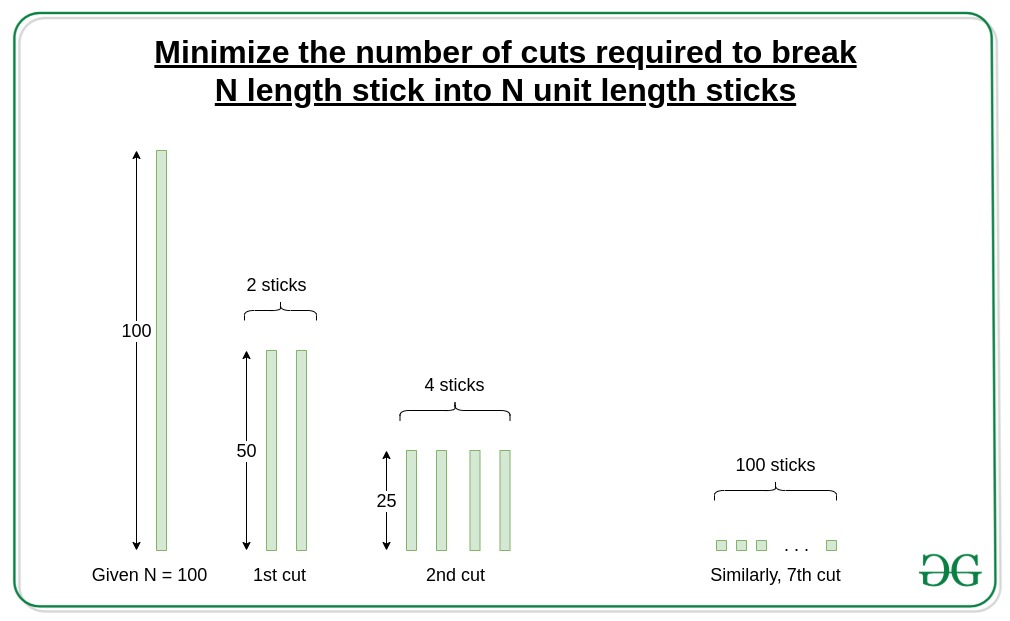
Hence, the minimum time required to split an N length stick into 1 unit pieces is ceil(log2N).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int min_time_to_cut(int N)
{
if (N == 0)
return 0;
return ceil(log2(N));
}
int main()
{
int N = 100;
cout << min_time_to_cut(N);
return 0;
}
|
Java
import java.lang.*;
class GFG{
static int min_time_to_cut(int N)
{
if (N == 0)
return 0;
return (int)Math.ceil(Math.log(N) /
Math.log(2));
}
public static void main(String[] args)
{
int N = 100;
System.out.print(min_time_to_cut(N));
}
}
|
Python3
import math
def min_time_to_cut(N):
if (N == 0):
return 0
return int(math.log2(N)) + 1
N = 100
print(min_time_to_cut(N))
|
C#
using System;
class GFG{
static int min_time_to_cut(int N)
{
if (N == 0)
return 0;
return (int)Math.Ceiling(Math.Log(N) /
Math.Log(2));
}
public static void Main()
{
int N = 100;
Console.Write(min_time_to_cut(N));
}
}
|
Javascript
<script>
function min_time_to_cut(N)
{
if (N == 0)
return 0;
return Math.ceil(Math.log(N) /
Math.log(2));
}
let N = 100;
document.write(min_time_to_cut(N));
</script>
|
Time Complexity: O (1)
Auxiliary Space: O (1)
Share your thoughts in the comments
Please Login to comment...