Maximum number of region in which N non-parallel lines can divide a plane

Given N‘, the number of non-parallel lines. The task is to find the maximum number of regions in which these lines can divide a plane.
Examples:

Input : N = 3
Output : 7
Input : N = 2
Output : 4

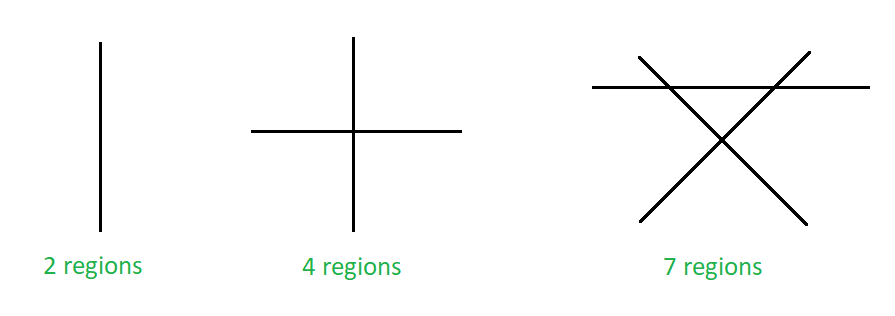
Maximum number of regions on a plane formed due to non-parallel lines

Approach: The above image shows the maximum number of regions a line can divide a plane. One line can divide a plane into two regions, two non-parallel lines can divide a plane into 4 regions and three non-parallel lines can divide into 7 regions, and so on. When the n^th line is added to a cluster of (n-1) lines then the maximum number of extra regions formed is equal to n.
Now solve the recursion as follows:

L(2) – L(1) = 2 … (i)
L(3) – L(2) = 3 … (ii)
L(4) – L(3) = 4 … (iii)
. . .
. . .
L(n) – L(n-1) = n ; … (n)
Adding all the above equation we get,
L(n) – L(1) = 2 + 3 + 4 + 5 + 6 + 7 + …… + n ;
L(n) = L(1) + 2 + 3 + 4 + 5 + 6 + 7 + …… + n ;
L(n) = 2 + 2 + 3 + 4 + 5 + 6 + 7 + …… + n ;
L(n) = 1 + 2 + 3 + 4 + 5 + 6 + 7 + …… + n + 1 ;
L(n) = n ( n + 1 ) / 2 + 1 ;

The number of region in which N non-parallel lines can divide a plane is equal to N*( N + 1 )/2 + 1.
Below is the implementation of the above approach:

C++

// C++ program to implement the above problem
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the maximum
// number of regions on a plane
void maxRegions(int n)
{
    int num;
    num = n * (n + 1) / 2 + 1;
 
    // print the maximum number of regions
    cout << num;
}
 
// Driver code
int main()
{
    int n = 10;
 
    maxRegions(n);
 
    return 0;
}

Java

// Java program to implement the above problem
class GFG
{
 
    // Function to find the maximum
    // number of regions on a plane
    static void maxRegions(int n)
    {
        int num;
        num = n * (n + 1) / 2 + 1;
 
        // print the maximum number of regions
        System.out.println(num);;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 10;
        maxRegions(n);
    }
}
 
// This code is contributed by 29AjayKumar

Python3

# Python3 program to implement
# the above problem
 
# Function to find the maximum
# number of regions on a plane
def maxRegions(n):
    num = n * (n + 1) // 2 + 1
 
    # print the maximum number
    # of regions
    print(num)
 
# Driver code
n = 10
 
maxRegions(n)
 
# This code is contributed
# by Mohit Kumar

C#

// C# program to implement the above problem
using System;
     
class GFG
{
 
    // Function to find the maximum
    // number of regions on a plane
    static void maxRegions(int n)
    {
        int num;
        num = n * (n + 1) / 2 + 1;
 
        // print the maximum number of regions
        Console.WriteLine(num);
    }
 
    // Driver code
    public static void Main(String[] args)
    {
        int n = 10;
        maxRegions(n);
    }
}
 
// This code is contributed by 29AjayKumar

Javascript

<script>
 
// Javascript program to implement the above problem
 
// Function to find the maximum
// number of regions on a plane
function maxRegions(n)
{
    let num;
    num = parseInt( n * (n + 1) / 2) + 1;
 
    // print the maximum number of regions
    document.write(num);
}
 
// Driver code
    let n = 10;
 
    maxRegions(n);
 
</script>