Mathematical Approach to PCA
Last Updated :
25 Aug, 2022
The main guiding principle for Principal Component Analysis is FEATURE EXTRACTION i.e. “Features of a data set should be less as well as the similarity between each other is very less.” In PCA, a new set of features are extracted from the original features which are quite dissimilar in nature. So, an n-dimensional feature space gets transformed into an m-dimensional feature space., where the dimensions are orthogonal to each other.
Concept of Orthogonality: (In order to understand this topic, we have to go to the vector space concept in linear algebra) Vector Space is a set of vectors. They can be represented as a linear combination of the smaller set of vectors called BASIS VECTORS. So any vector ‘v’ in a vector space can be represented as:
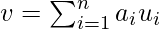
where a represent ‘n’ scalars and u represents the basis vectors. Basis vectors are orthogonal to each other. Orthogonality of vectors can be thought of an extension of the vectors being perpendicular in a 2-D vector space. So our feature vector (data-set) can be transformed into a set of principal components (just like the basis vectors).
Objectives of PCA:
- The new features are distinct i.e. the covariance between the new features (in case of PCA, they are the principal components) is 0.
- The principal components are generated in order of the variability in the data that it captures. Hence, the first principal component should capture the maximum variability, the second one should capture the next highest variability etc.
- The sum of the variance of the new features / the principal components should be equal to the sum of the variance of the original features.
Working of PCA:
PCA works on a process called Eigenvalue Decomposition of a covariance matrix of a data set. The steps are as follows:
- First, calculate the covariance matrix of a data set.
- Then, calculate the eigenvectors of the covariance matrix.
- The eigenvector having the highest eigenvalue represents the direction in which there is the highest variance. So this will help in identifying the first principal component.
- The eigenvector having the next highest eigenvalue represents the direction in which data has the highest remaining variance and also orthogonal to the first direction. So, this helps in identifying the second principal component.
- Like this, identify the top ‘k’ eigenvectors having top ‘k’ eigenvalues to get the ‘k’ principal components.
Numerical for PCA :
Consider the following dataset
| x1 | 2.5 | 0.5 | 2.2 | 1.9 | 3.1 | 2.3 | 2.0 | 1.0 | 1.5 | 1.1 |
| x2 | 2.4 | 0.7 | 2.9 | 2.2 | 3.0 | 2.7 | 1.6 | 1.1 | 1.6 | 0.9 |
Step 1: Standardize the Dataset
Mean for 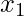 = 1.81 =
= 1.81 = 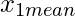
Mean for 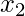 = 1.91 =
= 1.91 = 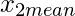
We will change the dataset.
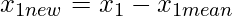 | 0.69 | -1.31 | 0.39 | 0.09 | 1.29 | 0.49 | 0.19 | -0.81 | -0.31 | -0.71 |
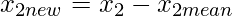 | 0.49 | -1.21 | 0.99 | 0.29 | 1.09 | 0.79 | -0.31 | -0.81 | -0.31 | -1.01 |
Step 2: Find the Eigenvalues and eigenvectors
Correlation Matrix c = 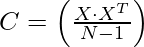
where, X is the Dataset Matrix (In this numerical, it is a 10 X 2 matrix)
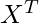 is the transpose of the X (In this numerical, it is a 2 X 10 matrix) and N is the number of elements = 10
is the transpose of the X (In this numerical, it is a 2 X 10 matrix) and N is the number of elements = 10
So, 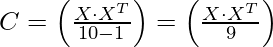
{So in order to calculate the Correlation Matrix, we have to do the multiplication of the Dataset Matrix with its transpose}
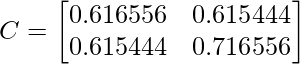
Using the equation, | C – 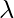 I | = 0– equation (i) where { \lambda is the eigenvalue and I is the Identity Matrix }
I | = 0– equation (i) where { \lambda is the eigenvalue and I is the Identity Matrix }
So solving equation (i)
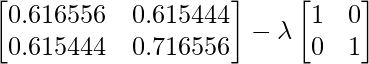
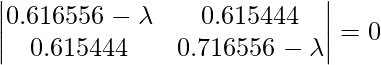
Taking the determinant of the left side, we get
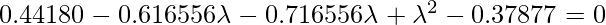
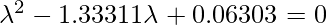
We get two values for 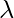 , that are (
, that are (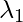 ) = 1.28403 and (
) = 1.28403 and (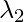 ) = 0.0490834. Now we have to find the eigenvectors for the eigenvalues
) = 0.0490834. Now we have to find the eigenvectors for the eigenvalues 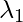 and
and 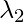
To find the eigenvectors from the eigenvalues, we will use the following approach:
First, we will find the eigenvectors for the eigenvalue 1.28403 by using the equation 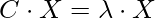
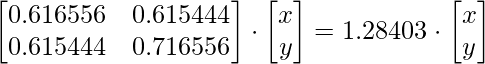
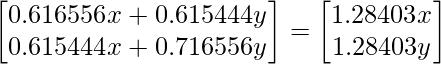
Solving the matrices, we get
0.616556x + 0.615444y = 1.28403x ; x = 0.922049 y
(x and y belongs to the matrix X) so if we put y = 1, x comes out to be 0.922049. So now the updated X matrix will look like:
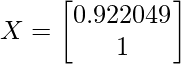
IMP: Till now we haven’t reached to the eigenvectors, we have to a bit of modifications in the X matrix. They are as follows:
A. Find the square root of the sum of the squares of the element in X matrix i.e.
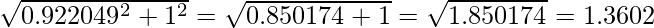
B. Now divide the elements of the X matrix by the number 1.3602 (just found that)
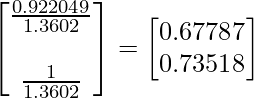
So now we found the eigenvectors for the eigenvector 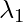 , they are 0.67787 and 0.73518
, they are 0.67787 and 0.73518
Secondly, we will find the eigenvectors for the eigenvalue 0.0490834 by using the equation {Same approach as of previous step)
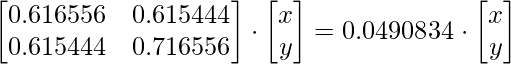
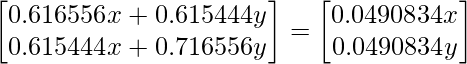
Solving the matrices, we get
0.616556x + 0.615444y = 0.0490834x; y = -0.922053
(x and y belongs to the matrix X) so if we put x = 1, y comes out to be -0.922053 So now the updated X matrix will look like:
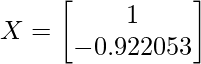
IMP: Till now we haven’t reached to the eigenvectors, we have to a bit of modifications in the X matrix. They are as follows:
A. Find the square root of the sum of the squares of the elements in X matrix i.e.
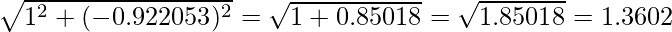
B. Now divide the elements of the X matrix by the number 1.3602 (just found that)
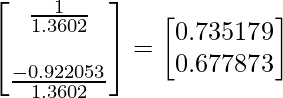
So now we found the eigenvectors for the eigenvector \lambda_2, they are 0.735176 and 0.677873
Sum of eigenvalues (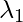 ) and (
) and (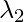 ) = 1.28403 + 0.0490834 = 1.33 = Total Variance {Majority of variance comes from
) = 1.28403 + 0.0490834 = 1.33 = Total Variance {Majority of variance comes from 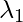 }
}
Step 3: Arrange Eigenvalues
The eigenvector with the highest eigenvalue is the Principal Component of the dataset. So in this case, eigenvectors of lambda1 are the principal components.
{Basically in order to complete the numerical we have to only solve till this step, but if we have to prove why we have chosen that particular eigenvector we have to follow the steps from 4 to 6}
Step 4: Form Feature Vector
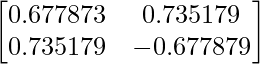 This is the FEATURE VECTOR for Numerical
This is the FEATURE VECTOR for Numerical
Where first column are the eigenvectors of 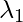 & second column are the eigenvectors of
& second column are the eigenvectors of 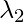
Step 5: Transform Original Dataset
Use the equation Z = X V

Step 6: Reconstructing Data
Use the equation X = 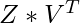 (
(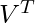 is Transpose of V), X = Row Zero Mean Data
is Transpose of V), X = Row Zero Mean Data

So in order to reconstruct the original data, we follow:
Row Original DataSet = Row Zero Mean Data + Original Mean

So for the eigenvectors of first eigenvalue, data can be reconstructed similar to the original dataset. Thus we can say that the Principal Component of the dataset is 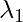 is 1.28403 followed by
is 1.28403 followed by 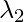 that is 0.0490834
that is 0.0490834
Share your thoughts in the comments
Please Login to comment...