Magnetic Field due to Current in Straight Wire
Last Updated :
03 Feb, 2022
All the magnetic fields that are known are due to current charges (or moving charges). A current-carrying wire produces a magnetic field because inside the conductor charges are moving. This can also be verified by a simple experiment of keeping a magnetic compass near any current-carrying wire. There are different types and shapes of current-carrying conductors. The shape of the conductor affects the magnetic field that is produced by it. To further understand the nature and behavior of the magnetic field produced by these conductors, it is essential to formulate the theory behind these concepts. Let’s see them in detail.
Magnetic Fields due to Moving Charges
Moving charges produce a magnetic field. In a conductor carrying current, charges are always moving and thus such conductors produce magnetic fields around them. The field that is produced by these charges can be visualized in the figure below. The direction of this magnetic field is given by the right-hand thumb rule. In this rule, the thumb of the right-hand points in the direction of the current. The curled fingers give the direction of the magnetic field around the wire.

The magnetic fields produced by a current loop and solenoid are shown in the figure below:


Biot-Savart Law
Biot-Savart law establishes the relationship between the electric current and the magnetic field produced by it. The figure shown below shows a current-carrying conductor in space. Let us denote the current that the conductor is carrying by “I”. Consider “dl” as an infinitesimally small part of the conductor. Then, the magnetic field dB at a point P due to this current carrying element at distance “r” will be given by,
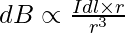

This is a cross product. The magnitude of this field is given by,
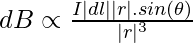
In this case, the θ is the angle between the vectors “dl” and “r”.
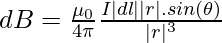
The proportionality constant 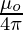 has an exact value of 10-7. Where µ0 is called the permeability of a free space or a vacuum.
has an exact value of 10-7. Where µ0 is called the permeability of a free space or a vacuum.
Similarities between Coulomb’s law and Biot-Savart Law
Biot-Savart law has some similarities as well as some differences with Coulomb’s law from electrostatic theory. Both the laws depend on the inverse of the squared distance. The principle of superposition is applicable to both of these laws. The only difference comes in the fact that the electrostatic force is a scalar quantity while the magnetic field is a vector quantity that depends on the cross product.
Magnetic Field due to a straight current-carrying wire
The magnitude and the direction of the magnetic field due to the straight current-carrying wire can be calculated using the Biot-Savart law mentioned above. Consider “I” as the current flowing in the straight wire, and “r” be the distance. Then the magnetic field produced by the wire at that particular point is given by.
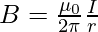
Since the wire is assumed to be very long, the magnitude of the magnetic field depends on the distance of the point from the wire rather than the position along the wire.
Sample Problems
Question 1: A straight current-carrying conductor is carrying a current of 10A. Find the magnitude of the magnetic field produced by it at a distance of 2 m.
Answer:
The magnitude of the magnetic field produced by a current carrying straight wire is given by,
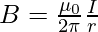
Given:
r = 2 m, I = 10A.
Plugging in the values into the equation,
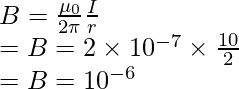
Question 2: A straight current-carrying conductor is carrying a current of 5A. Find the magnitude of the magnetic field produced by it at a distance of 1 m.
Answer:
The magnitude of the magnetic field produced by a current carrying straight wire is given by,
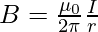
Given:
r = 1 m, I = 5A.
Plugging in the values into the equation,
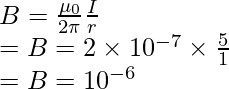
Question 3: A straight current-carrying conductor produces a magnetic field of 5T at a distance of 2 m. Find the magnitude of the electric current flowing through it.
Answer:
The magnitude of the magnetic field produced by a current carrying straight wire is given by,
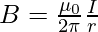
Given:
r = 2 m, B = 5.
Plugging in the values into the equation,
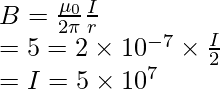
Question 4: A straight current-carrying conductor is carrying a current of 10A and another conductor parallel to it carries a current of 5A on the opposite side as shown in the figure below. Find the magnitude of the magnetic field produced by the system at a distance of 2 m.

Answer:
The magnetic fields follow the principle of super-position. The total magnetic field,
B = B1 + B2
The magnitude of the magnetic field produced by a current carrying straight wire is given by,
r = 2 m, I = 10A.
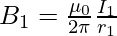
Plugging in the values into the equation,
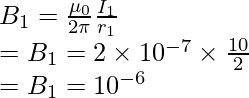
For the second wire, r = 4 m, I = 5A
Plugging in the values into the equation,
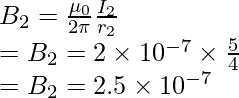
B = B1 – B2
⇒ B = 10-6 – 0.25 × 10-6
⇒ B = 0.75 × 10-6
Question 5: A straight current-carrying conductor is carrying a current of 10A and another conductor parallel to it carries a current of 10A in the same direction as shown in the figure below. Find the magnitude of the magnetic field produced by the system at a distance of 2 m.

Answer:
The magnetic fields follow the principle of super-position. The total magnetic field,
B = B1 + B2
The magnitude of the magnetic field produced by a current carrying straight wire is given by,
r = 2 m, I = 10A.
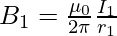
Plugging in the values into the equation,
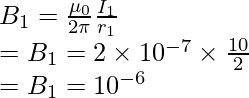
For the second wire, r = 4 m, I = 5A
Plugging in the values into the equation,
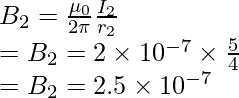
B = B1 + B2
⇒ B = 10-6 + 0.25 × 10-6
⇒ B = 1.25 × 10-6
Share your thoughts in the comments
Please Login to comment...