Magnetic Force on a Current carrying Wire
Last Updated :
21 Jul, 2021
When a charge is moving under the influence of a magnetic field. It experiences forces, which are perpendicular to its movement. This property of charge is exploited in a lot of fields, for example, this phenomenon is used in the making of motors which in turn are useful for producing mechanical forces. These forces are governed by the right-hand thumb rule and are given by the vector products. When a current-carrying wire is exposed to the magnetic field it also experiences forces because the charges are moving inside the conductor.
Force on a Moving Charge in a Magnetic Field
Consider the figure below, this figure shows a conductor that is under the influence of a magnetic field. The conductor is connected to a battery that is continuously causing the current to flow in the wire and the conductor. Since the charges are moving inside the conductor, these charges start experiencing force. Now, these charges are in the conductor and cannot go outside, so the force exerted on these charges is in turn transferred to the force being applied on the conductor.

The direction of the force experienced by the conductor is given by the right-hand thumb rule. Now let’s focus on deriving the formula for calculating the force on a current-carrying conductor.
Force acting on each charge flowing inside the conductor in the region where the magnetic field is acting. The total force in this case can be calculated by taking a sum of magnetic forces on the individual charges. Since all the forces will be acting in the same direction, the force on the charges can be added. Consider an individual charge moving with a drift velocity vd. The force acting on this charge is given by,
F = qvBsin(θ)
Considering the magnetic field B, to be uniform over the length “l” of the wire and zero everywhere else. The total magnetic force on the wire, in that case, will be given by,
F = 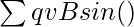
Since, each charge is moving with equal velocity, the total force can be re-written as,
F = qvBsin(θ)N
Where N is the number of charges under the influence of the magnetic field. Let’s say “n” is the number of charge carriers per unit volume of the conductors and “V” is the volume of the region of the wire where the magnetic field is acting.
N = nV
Substituting this value in the equation above,
F = qvBsin(θ)(nV)
⇒ F = qvBsin(θ)nV
Also, since the wire is uniform the V = Al, where A is the cross-sectional area and l is the length of the wire under magnetic field. Plugging this value in the equation,
F = qvBsin(θ)nAl
This can be re-arranged as,
F = (nqAv)lBsin(θ)
It is known that nqAv = i, where i is the current in the conductor.
So, the force becomes,
F = ilBsin(θ)
In terms of vector product, this force is given by,
F = i(L × B)
The figure below represents the direction of the force, notice that the direction of the force is perpendicular to both the magnetic field and the direction in which the conductor is carrying current.

Let’s look at some sample problems.
Sample Problems
Question 1: Explain Fleming’s Left-hand Rule.
Answer:
Fleming’s Left-hand rule is used to find the direction of Force. If we put our left thumb, Index finger and middle finger perpendicular to each other in the 3-D space, the thumb will give the direction of the Force, the middle finger will give the direction of current and the Index finger will give the direction of the Magnetic filed.
Question 2: Calculate the force on the wire, given B = 1.50 T, l = 5.00 cm, and I = 20.0 A. The angle between the current and the magnetic field is 90°.
Answer:
The force on the current carrying conductor is given by,
F = ilBsin(θ)
Where, i = 20A, B = 1.5T and l = 5 cm and θ = 90°.
Plugging these values into the equation,
F = ilBsin(θ)
⇒ F = (20)(0.05)(1.5)sin(90°)
⇒ F = (1)(1.5)(1)
⇒ F = 1.5N
Question 3: Calculate the force on the wire, given B = 3 T, l = 50.00 cm, and I = 10.0 A. The angle between the current and the magnetic field is 30°.
Answer:
The force on the current carrying conductor is given by,
F = ilBsin(θ)
Where, i = 10A, B = 3T and l = 0.5 m and θ = 90°.
Plugging these values into the equation,
F = ilBsin(θ)
⇒ F = (10)(0.5)(3)sin(30°)
⇒ F = (5)(0.5)(3)
⇒ F = 7.5N
Question 4: What is the angle between a wire carrying a 4.00-A current and the 2-T field it is in if 50.0 cm of the wire experiences a magnetic force of 8.0 N?
Answer:
The force on the current carrying conductor is given by,
F = ilBsin(θ)
Where, i = 4A, B = 2T and l = 2 m, θ = ? And F = 8.0N
Plugging these values into the equation,
F = ilBsin(θ)
⇒ 8 = (4)(2)(2)sin(θ)
⇒ 8 = 16sin(θ)
⇒ 0.5 = sin(θ)
⇒ sin-1(0.5) = θ
⇒ θ = 30°
Question 5: What is the current in a wire carrying under the 3-T field it is in if 50.0 cm of the wire experiences a magnetic force of 12 N and the angle between the magnetic field and current is 30°?
Answer:
The force on the current carrying conductor is given by,
F = ilBsin(θ)
Where, i =?, B = 3T and l = 0.5 m , θ = 30° and F = 12N
Plugging these values into the equation,
F = ilBsin(θ)
⇒ 12 = (i)(0.5)(3)sin(30°)
⇒ 12(2) = i1.5
⇒ i= 16A
Share your thoughts in the comments
Please Login to comment...