LRU Cache implementation using Double Linked Lists
Last Updated :
11 Oct, 2023
Given an integer N represents the size of the doubly linked list and array arr[], where arr[i] is the element to be search within the linked list, the task is to use a doubly linked list to implement the Least Recently Used (LRU) algorithm.
Examples:
Input: N = 3, Arr = { 1, 2, 3 }
Output:
[0]->[0]->[0]->NULL
[1]->[0]->[0]->NULL
[2]->[1]->[0]->NULL
[3]->[2]->[1]->NULL
Input: N = 5, Arr = { 1, 2, 3, 4, 3, 8 }
Output:
[0]->[0]->[0]->[0]->[0]->NULL
[1]->[0]->[0]->[0]->[0]->NULL
[2]->[1]->[0]->[0]->[0]->NULL
[3]->[2]->[1]->[0]->[0]->NULL
[4]->[3]->[2]->[1]->[0]->NULL
[2]->[4]->[3]->[1]->[0]->NULL
[8]->[2]->[4]->[3]->[1]->NULL
Illustration:
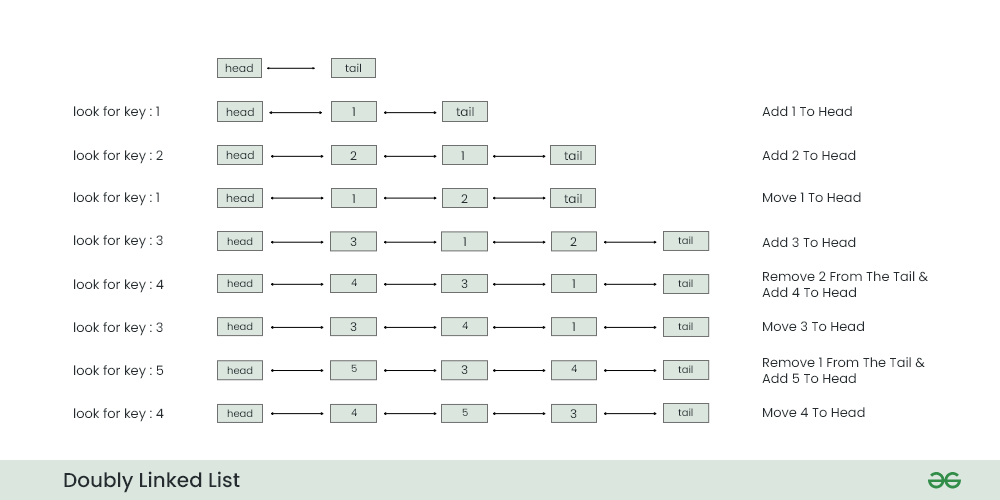
Let’s suppose we have an LRU cache with capacity 3, we would like to perform search operations on the cache given by arr[] = {1, 2, 1, 3, 4, 3, 5, 4}.
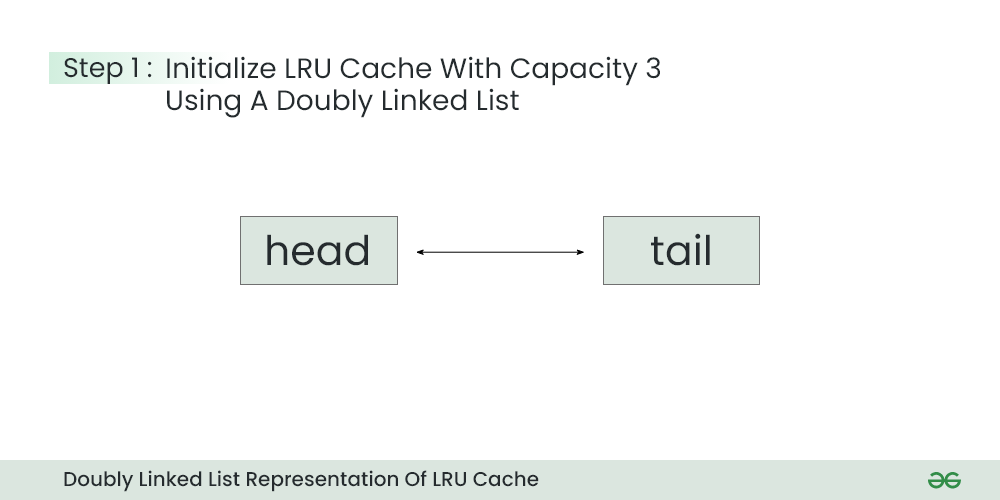
Step 1) Initialize the Cache:
- During this step we create an empty doubly linked list with only head and tail pointing to each other.
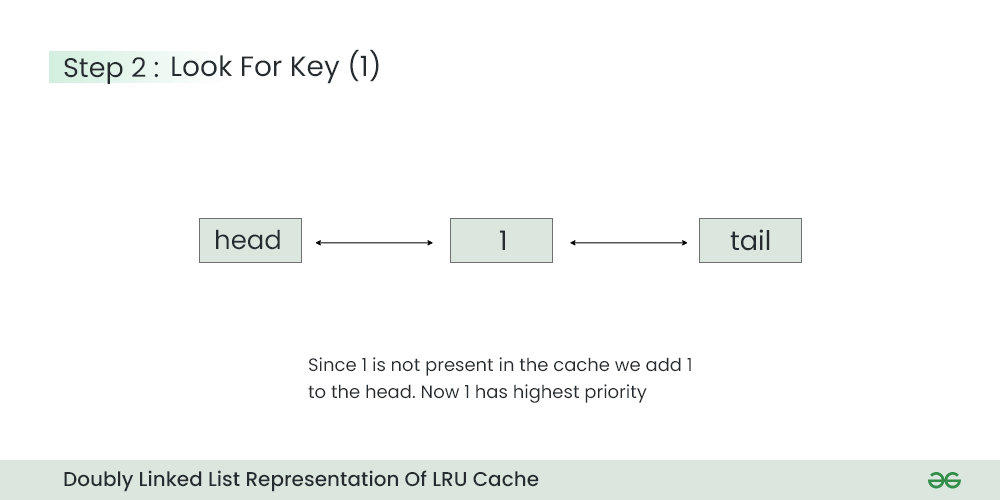
Step 2) Look for Key=1 in the cache
- Since key=1 is not present and cache is not full, we can put 1 after the head at this step.
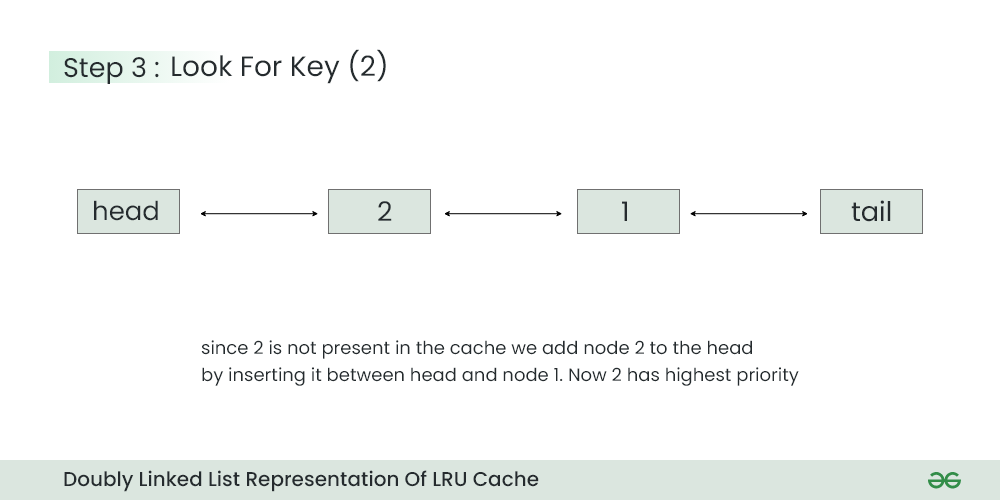
Step 3) Look for Key=2 in the cache
- Since key=2 is not present and cache is not full, we can put key=2 after the head at this step. Notice that priority of key=1 has been decreased now.
Step 4) Look for Key=1 in the cache
- Since key=1 is present, we can simply return 1 and update the priority of 1 to highest priority.

Step 5) Look for Key=3 in the cache
- Since key=3 is not present and there is a space in our cache, so we can simply put 3 after the head. Now after this step our Cache is full and the order of priority is 3>1>2.

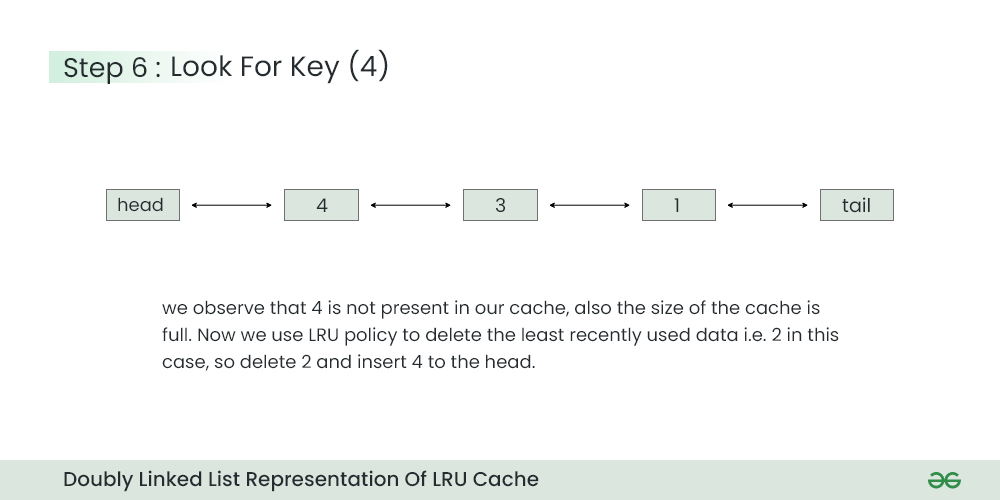
Step 6) Look for Key=4 in the cache
- Since key=4 is not present and the size of cache is full, apply LRU algorithm to remove the least recently used key (i.e. 2) and then attach 4 after the head. The new order of priority after this operation will be 4>3>1.
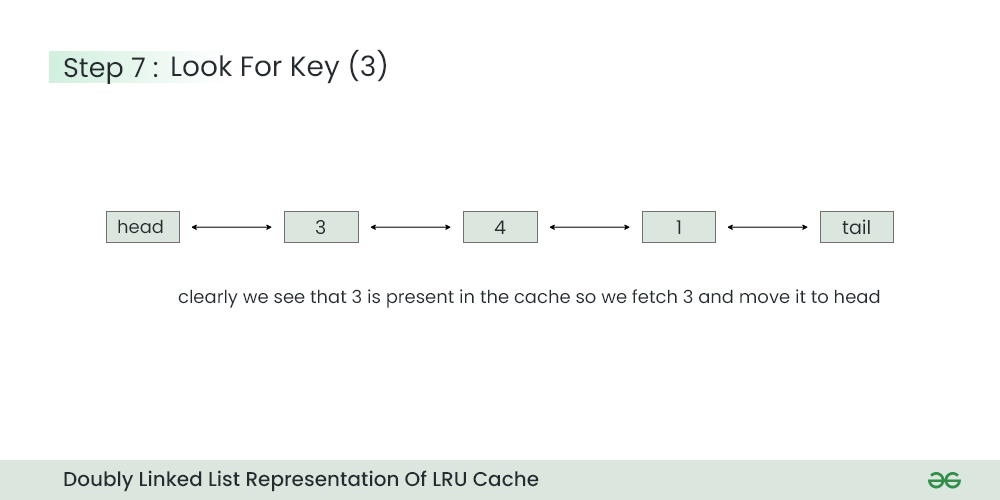
Step 7) Look for Key=3 in the cache
- Since key=3 is present then simply fetch it from the cache and update the priority to 3>4>1.
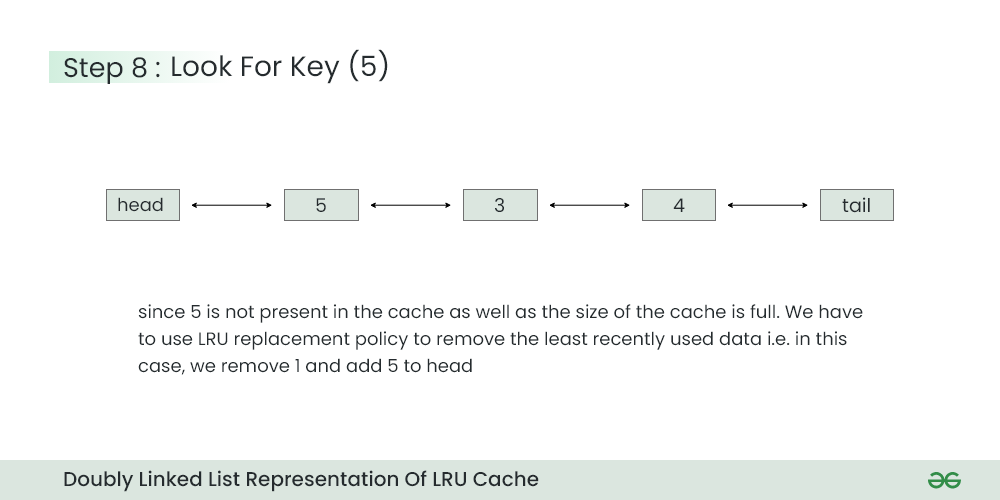
Step 8) Look for Key=5 in the cache
- Since key=5 is not present and the size of cache is also full, we apply LRU algorithm to remove the least recently used key (i.e. 1) and attach 5 after the head. The new order of priority after this operation will be 5>3>4.
Step 9) Look for Key=4 in the cache
- Since key=4 is present then simply fetch it from the cache and update the priority to 4>5>3.

All the above operations are summarised in the below image:
Approach:
The idea is very basic that keep inserting the elements at the head
- If the element is not present in the list the add it to the head of the list
- If the element is present in the list then move the element to the head and shift the remaining element of the list
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
struct doublelinkedlist {
int val;
struct doublelinkedlist* next;
struct doublelinkedlist* prev;
};
struct doublelinkedlist* head;
struct doublelinkedlist* tail;
struct doublelinkedlist* temp;
int status;
int AddNode(int value)
{
if (head == NULL) {
head = (struct doublelinkedlist*)malloc(
sizeof(struct doublelinkedlist));
if (head == NULL) {
cout << "Unable to allocate space\n";
return -2;
}
head->val = value;
tail = head;
head->prev = NULL;
}
else {
temp = tail;
tail->next = (struct doublelinkedlist*)malloc(
sizeof(struct doublelinkedlist));
if (tail->next == NULL) {
cout << "Unable to allocate space\n";
return -2;
}
tail->next->val = value;
tail = tail->next;
tail->prev = temp;
}
tail->next = NULL;
return 0;
}
int PrintCache(void)
{
if (head == NULL) {
cout << "Add a node first\n";
return -2;
}
else {
temp = head;
while (temp != NULL) {
cout << "[" << temp->val<<"]->";
temp = temp->next;
}
cout << "NULL\n";
}
return 0;
}
int GetKey(int value)
{
if (head == NULL) {
cout << "Add a node first\n";
return -1;
}
temp = head;
while (temp != NULL)
{
if (temp->val == value)
{
while (temp != head) {
temp->val = temp->prev->val;
temp = temp->prev;
}
head->val = value;
return 0;
}
temp = temp->next;
}
temp = tail->prev;
while (temp != NULL) {
temp->next->val = temp->val;
temp = temp->prev;
}
head->val = value;
return 0;
}
int NodesInLRU(int number)
{
static int i = 0;
for (i = 0; i < number; i += 1) {
status = AddNode(0);
if (status < 0) {
cout << "Could not assign node\n";
return status;
}
}
return 0;
}
void LRUOperations(int arr[], int n)
{
for (int i = 0; i < n; ++i) {
GetKey(arr[i]);
if (status < 0) {
exit(1);
}
status = PrintCache();
}
}
int main(void)
{
int CAPACITY = 5;
status = NodesInLRU(CAPACITY);
int n = 10;
int arr[] = { 1, 2, 3, 4, 5, 2, 10, 7, 11, 1 };
LRUOperations(arr, n);
return 0;
}
|
C
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>
struct doublelinkedlist {
int val;
struct doublelinkedlist* next;
struct doublelinkedlist* prev;
};
struct doublelinkedlist* head;
struct doublelinkedlist* tail;
struct doublelinkedlist* temp;
int status;
int AddNode(int value)
{
if (head == NULL) {
head = (struct doublelinkedlist*)
malloc(sizeof(struct doublelinkedlist));
if (head == NULL) {
printf("Unable to allocate space\n");
return -2;
}
head->val = value;
tail = head;
head->prev = NULL;
}
else {
temp = tail;
tail->next = (struct doublelinkedlist*)
malloc(sizeof(struct doublelinkedlist));
if (tail->next == NULL) {
printf("Unable to allocate space\n");
return -2;
}
tail->next->val = value;
tail = tail->next;
tail->prev = temp;
}
tail->next = NULL;
return 0;
}
int Display(void)
{
if (head == NULL) {
printf("Add a node first\n");
return -2;
}
else {
temp = head;
while (temp != NULL) {
printf("[%d]->", temp->val);
temp = temp->next;
}
printf("NULL\n");
}
return 0;
}
int SearchCache(int value)
{
if (head == NULL) {
printf("Add a node first\n");
return -1;
}
temp = head;
while (temp != NULL)
{
if (temp->val == value)
{
while (temp != head) {
temp->val = temp->prev->val;
temp = temp->prev;
}
head->val = value;
return 0;
}
temp = temp->next;
}
temp = tail->prev;
while (temp != NULL) {
temp->next->val = temp->val;
temp = temp->prev;
}
head->val = value;
return 0;
}
int NumberOfNodes(int number)
{
static int i = 0;
for (i = 0; i < number; i += 1) {
status = AddNode(0);
if (status < 0) {
printf("Could not assign node\n");
return status;
}
}
return 0;
}
int FreeCache(int number)
{
struct doublelinkedlist** freeing_ptr
= &head;
static int i = 0;
for (i = 0; i < number; i += 1) {
free(*freeing_ptr);
*freeing_ptr = NULL;
freeing_ptr += 1;
}
return 0;
}
void LRUOp(int arr[], int n)
{
for (int i = 0; i < n; ++i) {
SearchCache(arr[i]);
if (status < 0) {
exit(1);
}
status = Display();
}
}
int main(void)
{
int CAPACITY = 5;
status = NumberOfNodes(CAPACITY);
int n = 10;
int arr[] = { 1, 2, 3, 4, 5,
2, 10, 7, 11, 1 };
LRUOp(arr, n);
FreeCache(CAPACITY);
return 0;
}
|
Java
class DoubleLinkedListNode {
int val;
DoubleLinkedListNode next;
DoubleLinkedListNode prev;
public DoubleLinkedListNode(int val) {
this.val = val;
}
}
class LRUCache {
private DoubleLinkedListNode head;
private DoubleLinkedListNode tail;
private DoubleLinkedListNode temp;
private int status;
public LRUCache() {
head = null;
tail = null;
temp = null;
status = 0;
}
public int addNode(int value) {
if (head == null) {
head = new DoubleLinkedListNode(value);
tail = head;
head.prev = null;
} else {
temp = tail;
tail.next = new DoubleLinkedListNode(value);
tail = tail.next;
tail.prev = temp;
}
tail.next = null;
return 0;
}
public int display() {
if (head == null) {
System.out.println("Add a node first");
return -2;
} else {
temp = head;
StringBuilder str = new StringBuilder();
while (temp != null) {
str.append("[").append(temp.val).append("]->");
temp = temp.next;
}
System.out.println(str.toString() + "NULL");
}
return 0;
}
public int searchCache(int value) {
if (head == null) {
System.out.println("Add a node first");
return -1;
}
temp = head;
while (temp != null) {
if (temp.val == value) {
while (temp != head) {
temp.val = temp.prev.val;
temp = temp.prev;
}
head.val = value;
return 0;
}
temp = temp.next;
}
temp = tail.prev;
while (temp != null) {
temp.next.val = temp.val;
temp = temp.prev;
}
head.val = value;
return 0;
}
public int numberOfNodes(int number) {
for (int i = 0; i < number; i++) {
status = addNode(0);
if (status < 0) {
System.out.println("Could not assign node");
return status;
}
}
return 0;
}
public int freeCache() {
temp = head;
while (temp != null) {
head = head.next;
temp = head;
}
tail = null;
return 0;
}
public void lruOp(int[] arr, int n) {
for (int i = 0; i < n; i++) {
status = searchCache(arr[i]);
if (status < 0) {
System.exit(1);
}
status = display();
}
}
}
public class Main {
public static void main(String[] args) {
int MEMSIZE = 5;
LRUCache cache = new LRUCache();
cache.numberOfNodes(MEMSIZE);
int n = 10;
int[] arr = { 1, 2, 3, 4, 5, 2, 10, 7, 11, 1 };
cache.lruOp(arr, n);
cache.freeCache();
}
}
|
Python3
class doublelinkedlist:
def __init__(self, val=None, next=None, prev=None):
self.val = val
self.next = next
self.prev = prev
head = None
tail = None
temp = None
status = None
def AddNode(value):
global head, tail, temp
if head is None:
head = doublelinkedlist(value)
tail = head
head.prev = None
else:
temp = tail
tail.next = doublelinkedlist(value)
tail = tail.next
tail.prev = temp
tail.next = None
return 0
def Display():
global head, temp
if head is None:
print("Add a node first")
return -2
else:
temp = head
while temp is not None:
print(f"[{temp.val}]->", end="")
temp = temp.next
print("NULL")
return 0
def SearchCache(value):
global head, temp
if head is None:
print("Add a node first")
return -1
temp = head
while temp is not None:
if temp.val == value:
while temp != head:
temp.val = temp.prev.val
temp = temp.prev
head.val = value
return 0
temp = temp.next
temp = tail.prev
while temp is not None:
temp.next.val = temp.val
temp = temp.prev
head.val = value
return 0
def NumberOfNodes(number):
global status
for i in range(number):
status = AddNode(0)
if status < 0:
print("Could not assign node")
return status
return 0
def FreeCache(number):
global head, tail, temp
temp = head
while temp is not None:
head = head.next
del temp
temp = head
tail = None
return 0
def LRUOp(arr, n):
global status
for i in range(n):
status = SearchCache(arr[i])
if status < 0:
exit(1)
status = Display()
if __name__ == '__main__':
CAPACITY = 5
status = NumberOfNodes(CAPACITY)
n = 10
arr = [1, 2, 3, 4, 5, 2, 10, 7, 11, 1]
LRUOp(arr, n)
FreeCache(CAPACITY)
|
C#
using System;
class DoubleLinkedListNode
{
public int Val { get; set; }
public DoubleLinkedListNode Next { get; set; }
public DoubleLinkedListNode Prev { get; set; }
public DoubleLinkedListNode(int val = 0,
DoubleLinkedListNode next = null,
DoubleLinkedListNode prev = null)
{
Val = val;
Next = next;
Prev = prev;
}
}
class LRUCache
{
private DoubleLinkedListNode head;
private DoubleLinkedListNode tail;
private DoubleLinkedListNode temp;
private int status;
public LRUCache()
{
head = null;
tail = null;
temp = null;
status = 0;
}
public int AddNode(int value)
{
if (head == null)
{
head = new DoubleLinkedListNode(value);
tail = head;
head.Prev = null;
}
else
{
temp = tail;
tail.Next = new DoubleLinkedListNode(value);
tail = tail.Next;
tail.Prev = temp;
}
tail.Next = null;
return 0;
}
public int Display()
{
if (head == null)
{
Console.WriteLine("Add a node first");
return -2;
}
else
{
temp = head;
string str = "";
while (temp != null)
{
str += $"[{temp.Val}]->";
temp = temp.Next;
}
Console.WriteLine(str + "NULL");
}
return 0;
}
public int SearchCache(int value)
{
if (head == null)
{
Console.WriteLine("Add a node first");
return -1;
}
temp = head;
while (temp != null)
{
if (temp.Val == value)
{
while (temp != head)
{
temp.Val = temp.Prev.Val;
temp = temp.Prev;
}
head.Val = value;
return 0;
}
temp = temp.Next;
}
temp = tail.Prev;
while (temp != null)
{
temp.Next.Val = temp.Val;
temp = temp.Prev;
}
head.Val = value;
return 0;
}
public int NumberOfNodes(int number)
{
for (int i = 0; i < number; i++)
{
status = AddNode(0);
if (status < 0)
{
Console.WriteLine("Could not assign node");
return status;
}
}
return 0;
}
public int FreeCache()
{
temp = head;
while (temp != null)
{
head = head.Next;
temp = head;
}
tail = null;
return 0;
}
public void LRUOp(int[] arr, int n)
{
for (int i = 0; i < n; i++)
{
status = SearchCache(arr[i]);
if (status < 0)
{
Environment.Exit(1);
}
status = Display();
}
}
}
class Program
{
static void Main(string[] args)
{
int MEMSIZE = 5;
LRUCache cache = new LRUCache();
cache.NumberOfNodes(MEMSIZE);
int n = 10;
int[] arr = { 1, 2, 3, 4, 5, 2, 10, 7, 11, 1 };
cache.LRUOp(arr, n);
cache.FreeCache();
}
}
|
Javascript
class doublelinkedlist {
constructor(val = null, next = null, prev = null) {
this.val = val;
this.next = next;
this.prev = prev;
}
}
let head = null;
let tail = null;
let temp = null;
let status = null;
function AddNode(value) {
if (head === null) {
head = new doublelinkedlist(value);
tail = head;
head.prev = null;
} else {
temp = tail;
tail.next = new doublelinkedlist(value);
tail = tail.next;
tail.prev = temp;
}
tail.next = null;
return 0;
}
function Display() {
if (head === null) {
console.log("Add a node first");
return -2;
} else {
temp = head;
let str = "";
while (temp !== null) {
str += `[${temp.val}]->`;
temp = temp.next;
}
console.log(str + "NULL");
}
return 0;
}
function SearchCache(value) {
if (head === null) {
console.log("Add a node first");
return -1;
}
temp = head;
while (temp !== null) {
if (temp.val === value) {
while (temp !== head) {
temp.val = temp.prev.val;
temp = temp.prev;
}
head.val = value;
return 0;
}
temp = temp.next;
}
temp = tail.prev;
while (temp !== null) {
temp.next.val = temp.val;
temp = temp.prev;
}
head.val = value;
return 0;
}
function NumberOfNodes(number) {
for (let i = 0; i < number; i++) {
status = AddNode(0);
if (status < 0) {
console.log("Could not assign node");
return status;
}
}
return 0;
}
function FreeCache(number) {
temp = head;
while (temp !== null) {
head = head.next;
temp = head;
}
tail = null;
return 0;
}
function LRUOp(arr, n) {
for (let i = 0; i < n; i++) {
status = SearchCache(arr[i]);
if (status < 0) {
process.exit(1);
}
status = Display();
}
}
let CAPACITY = 5;
status = NumberOfNodes(CAPACITY);
let n = 10;
let arr = [1, 2, 3, 4, 5, 2, 10, 7, 11, 1];
LRUOp(arr, n);
FreeCache(CAPACITY);
|
Output
[1]->[0]->[0]->[0]->[0]->NULL
[2]->[1]->[0]->[0]->[0]->NULL
[3]->[2]->[1]->[0]->[0]->NULL
[4]->[3]->[2]->[1]->[0]->NULL
[5]->[4]->[3]->[2]->[1]->NULL
[2]->[5]->[4]->[3]->[1]->NULL
[10]->[2]->[5]->[4]-...
Complexity Analysis:
- Time Complexity:
- Adding a node: O(1)
- Displaying the linked list: O(N)
- Searching in the cache: O(N)
- Initializing cache: O(CAPACITY)
- Freeing cache: O(CAPCACITY)
- LRU operations loop: O(N^2)
- Auxiliary Space:
- Linked list nodes: O(N)
- Other variables: O(1)
Share your thoughts in the comments
Please Login to comment...