Lower Tail Test of Population Mean with Known Variance in R
Last Updated :
02 Jun, 2022
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis.
The conventional steps that are followed while formulating the hypothesis test, are listed as follows
State null hypothesis (Ho) and alternate hypothesis (Ha)
Collect a relevant sample of data to test the hypothesis.
Choose significance level for the hypothesis test.
Perform an appropriate statistical test.
Based on test statistics and p-value decide whether to reject or fail to reject your null hypothesis.
Conventionally, In a lower-tail test, the null hypothesis states that the true population mean (μo) is greater than the hypothesized mean value (μ). We fail to reject the null hypothesis if the test statistic is greater than the critical value at the chosen significance level. In this article let us discuss how to conduct a lower tail test of the population mean with known variance.
Here the assumption is the population variance σ2 is known. From Central Limit Theorem (CLT), the population. the sample means of all possible samples of a population approximately follow a normal distribution. Let us define the test statistic based on CLT as follows
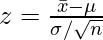
If z ≤−zα, where zα is the 100(1 − α) percentile of the standard normal distribution, we will have to reject the null hypothesis.
Let us try to understand the lower tail test by considering a case study.
Suppose the manufacturer claims that the mean lifetime of a tyre is more than 10,000 km. Assume the actual mean tyre lifetime is 9,950 km and the sample standard deviation is 120 km. At the .05 significance level, can we reject the manufacturer’s claim?
R
sample_mean = 9950
m0 = 10000
pop_std_dev = 120
sample_size = 30
z = (sample_mean-m0)/(pop_std_dev/sqrt(sample_size))
z
|
Output:
-2.28217
Now, let’s compute the critical value at a .05 significance level.
Code:
R
alpha = .05
z.alpha = qnorm(1-alpha)
-z.alpha
|
Output:
-1.6449
The test statistic -2.28217 is less than the critical value of -1.6449. Hence, at .05 significance level, we reject the claim that means a lifetime of a tyre is above 10,000 hours.
Share your thoughts in the comments
Please Login to comment...