Length of a Diagonal of a Parallelogram using the length of Sides and the other Diagonal
Last Updated :
22 Sep, 2022
Given two integers A and B, denoting the length of a parallelogram and an integer D, denoting the length of a diagonal, the task is to find the length of another diagonal of the parallelogram.
Examples:
Input: A = 10, B = 30, D = 20
Output: 40.0
Input: A = 6, B = 8, D = 10
Output: 10.0
Approach:
The relation between sides and diagonals of a parallelogram length of diagonal is given by the equation:
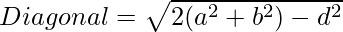
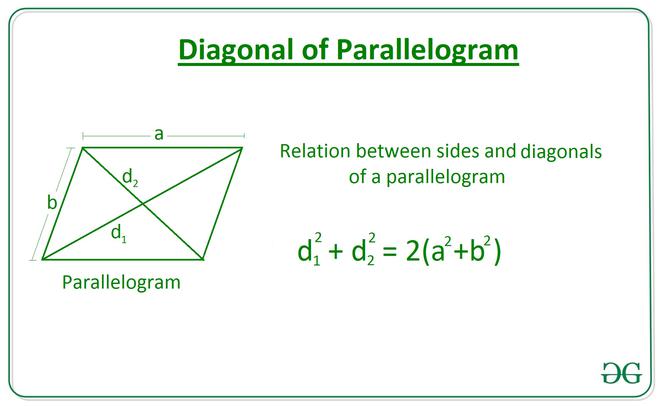
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float Length_Diagonal(int a, int b, int d)
{
float diagonal = sqrt(2 * ((a * a) +
(b * b)) - (d * d));
return diagonal;
}
int main()
{
int A = 10;
int B = 30;
int D = 20;
float ans = Length_Diagonal(A, B, D);
printf("%0.1f", ans);
return 0;
}
|
Java
class GFG{
static float Length_Diagonal(int a, int b, int d)
{
float diagonal = (float) Math.sqrt(2 * ((a * a) +
(b * b)) - (d * d));
return diagonal;
}
public static void main(String[] args)
{
int A = 10;
int B = 30;
int D = 20;
float ans = Length_Diagonal(A, B, D);
System.out.printf("%.1f", ans);
}
}
|
Python
import math
def Length_Diagonal(a, b, d):
diagonal = math.sqrt(2 * ((a**2) \
+ (b**2)) - (d**2))
return diagonal
A = 10
B = 30
D = 20
ans = Length_Diagonal(A, B, D)
print(round(ans, 2))
|
C#
using System;
class GFG{
static float Length_Diagonal(int a, int b, int d)
{
float diagonal = (float) Math.Sqrt(2 * ((a * a) +
(b * b)) - (d * d));
return diagonal;
}
public static void Main(String[] args)
{
int A = 10;
int B = 30;
int D = 20;
float ans = Length_Diagonal(A, B, D);
Console.Write("{0:F1}", ans);
}
}
|
Javascript
<script>
function Length_Diagonal( a, b, d)
{
let diagonal = Math.sqrt(2 * ((a * a) +
(b * b)) - (d * d));
return diagonal;
}
let A = 10;
let B = 30;
let D = 20;
let ans = Length_Diagonal(A, B, D);
document.write(ans.toFixed(1));
</script>
|
Time Complexity: O(logn) as using inbuilt sqrt function
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...