Newton Forward And Backward Interpolation

Interpolation is the technique of estimating the value of a function for any intermediate value of the independent variable, while the process of computing the value of the function outside the given range is called extrapolation.

Forward Differences: The differences y1 – y0, y2 – y1, y3 – y2, ……, yn – yn–1 when denoted by dy0, dy1, dy2, ……, dyn–1 are respectively, called the first forward differences. Thus, the first forward differences are : 

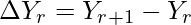
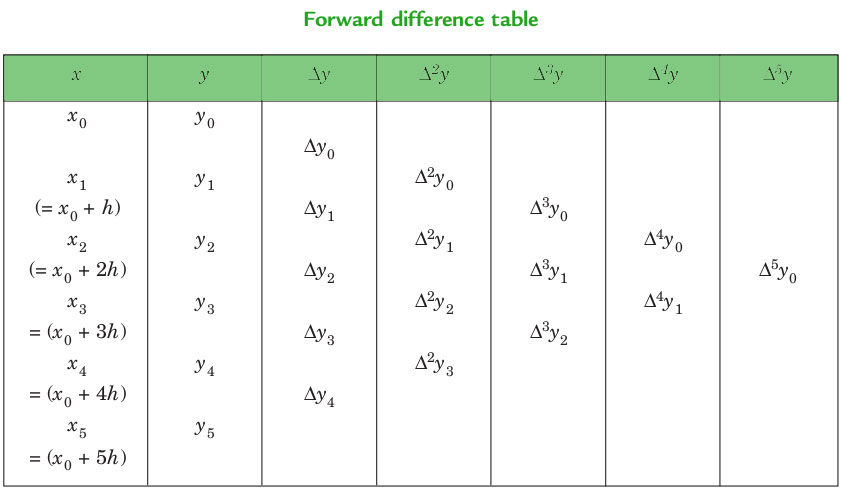
NEWTON’S GREGORY FORWARD INTERPOLATION FORMULA : 

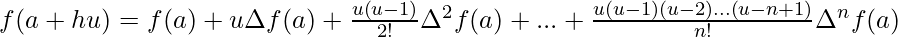
This formula is particularly useful for interpolating the values of f(x) near the beginning of the set of values given. h is called the interval of difference and u = ( x – a ) / h, Here a is the first term.

Example :  

Input : Value of Sin 52

Output :

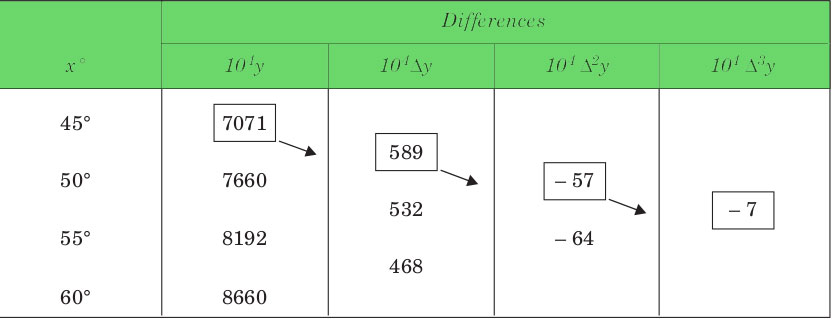
Value at Sin 52 is 0.788003

Below is the implementation of the Newton forward interpolation method. 

C++

// CPP Program to interpolate using
// newton forward interpolation
#include <bits/stdc++.h>
using namespace std;

// calculating u mentioned in the formula
float u_cal(float u, int n)
{
    float temp = u;
    for (int i = 1; i < n; i++)
        temp = temp * (u - i);
    return temp;
}

// calculating factorial of given number n
int fact(int n)
{
    int f = 1;
    for (int i = 2; i <= n; i++)
        f *= i;
    return f;
}

int main()
{
    // Number of values given
    int n = 4;
    float x[] = { 45, 50, 55, 60 };

    // y[][] is used for difference table
    // with y[][0] used for input
    float y[n][n];
    y[0][0] = 0.7071;
    y[1][0] = 0.7660;
    y[2][0] = 0.8192;
    y[3][0] = 0.8660;

    // Calculating the forward difference
    // table
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < n - i; j++)
            y[j][i] = y[j + 1][i - 1] - y[j][i - 1];
    }

    // Displaying the forward difference table
    for (int i = 0; i < n; i++) {
        cout << setw(4) << x[i]
             << "\t";
        for (int j = 0; j < n - i; j++)
            cout << setw(4) << y[i][j]
                 << "\t";
        cout << endl;
    }

    // Value to interpolate at
    float value = 52;

    // initializing u and sum
    float sum = y[0][0];
    float u = (value - x[0]) / (x[1] - x[0]);
    for (int i = 1; i < n; i++) {
        sum = sum + (u_cal(u, i) * y[0][i]) /
                                 fact(i);
    }

    cout << "\n Value at " << value << " is "
         << sum << endl;
    return 0;
}

Java

// Java Program to interpolate using
// newton forward interpolation

class GFG{
// calculating u mentioned in the formula
static double u_cal(double u, int n)
{
    double temp = u;
    for (int i = 1; i < n; i++)
        temp = temp * (u - i);
    return temp;
}

// calculating factorial of given number n
static int fact(int n)
{
    int f = 1;
    for (int i = 2; i <= n; i++)
        f *= i;
    return f;
}

public static void main(String[] args)
{
    // Number of values given
    int n = 4;
    double x[] = { 45, 50, 55, 60 };

    // y[][] is used for difference table
    // with y[][0] used for input
    double y[][]=new double[n][n];
    y[0][0] = 0.7071;
    y[1][0] = 0.7660;
    y[2][0] = 0.8192;
    y[3][0] = 0.8660;

    // Calculating the forward difference
    // table
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < n - i; j++)
            y[j][i] = y[j + 1][i - 1] - y[j][i - 1];
    }

    // Displaying the forward difference table
    for (int i = 0; i < n; i++) {
        System.out.print(x[i]+"\t");
        for (int j = 0; j < n - i; j++)
            System.out.print(y[i][j]+"\t");
        System.out.println();
    }

    // Value to interpolate at
    double value = 52;

    // initializing u and sum
    double sum = y[0][0];
    double u = (value - x[0]) / (x[1] - x[0]);
    for (int i = 1; i < n; i++) {
        sum = sum + (u_cal(u, i) * y[0][i]) /
                                fact(i);
    }

    System.out.println("\n Value at "+value+" is "+String.format("%.6g%n",sum));
}
}
// This code is contributed by mits

Python3

# Python3 Program to interpolate using
# newton forward interpolation

# calculating u mentioned in the formula
def u_cal(u, n):

    temp = u;
    for i in range(1, n):
        temp = temp * (u - i);
    return temp;

# calculating factorial of given number n
def fact(n):
    f = 1;
    for i in range(2, n + 1):
        f *= i;
    return f;

# Driver Code

# Number of values given
n = 4;
x = [ 45, 50, 55, 60 ];

# y[][] is used for difference table
# with y[][0] used for input
y = [[0 for i in range(n)]
        for j in range(n)];
y[0][0] = 0.7071;
y[1][0] = 0.7660;
y[2][0] = 0.8192;
y[3][0] = 0.8660;

# Calculating the forward difference
# table
for i in range(1, n):
    for j in range(n - i):
        y[j][i] = y[j + 1][i - 1] - y[j][i - 1];

# Displaying the forward difference table
for i in range(n):
    print(x[i], end = "\t");
    for j in range(n - i):
        print(y[i][j], end = "\t");
    print("");

# Value to interpolate at
value = 52;

# initializing u and sum
sum = y[0][0];
u = (value - x[0]) / (x[1] - x[0]);
for i in range(1,n):
    sum = sum + (u_cal(u, i) * y[0][i]) / fact(i);

print("\nValue at", value,
      "is", round(sum, 6));

# This code is contributed by mits

C#

// C# Program to interpolate using
// newton forward interpolation
using System;

class GFG
{
// calculating u mentioned in the formula
static double u_cal(double u, int n)
{
    double temp = u;
    for (int i = 1; i < n; i++)
        temp = temp * (u - i);
    return temp;
}

// calculating factorial of given number n
static int fact(int n)
{
    int f = 1;
    for (int i = 2; i <= n; i++)
        f *= i;
    return f;
}

// Driver code
public static void Main()
{
    // Number of values given
    int n = 4;
    double[] x = { 45, 50, 55, 60 };

    // y[,] is used for difference table
    // with y[,0] used for input
    double[,] y=new double[n,n];
    y[0,0] = 0.7071;
    y[1,0] = 0.7660;
    y[2,0] = 0.8192;
    y[3,0] = 0.8660;

    // Calculating the forward difference
    // table
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < n - i; j++)
            y[j,i] = y[j + 1,i - 1] - y[j,i - 1];
    }

    // Displaying the forward difference table
    for (int i = 0; i < n; i++) {
        Console.Write(x[i]+"\t");
        for (int j = 0; j < n - i; j++)
            Console.Write(y[i,j]+"\t");
        Console.WriteLine();
    }

    // Value to interpolate at
    double value = 52;

    // initializing u and sum
    double sum = y[0,0];
    double u = (value - x[0]) / (x[1] - x[0]);
    for (int i = 1; i < n; i++) {
        sum = sum + (u_cal(u, i) * y[0,i]) /
                                fact(i);
    }

    Console.WriteLine("\n Value at "+value+" is "+Math.Round(sum,6));
}
}
// This code is contributed by mits

PHP

<?php
// PHP Program to interpolate using
// newton forward interpolation

// calculating u mentioned in the formula
function u_cal($u, $n)
{
    $temp = $u;
    for ($i = 1; $i < $n; $i++)
        $temp = $temp * ($u - $i);
    return $temp;
}

// calculating factorial of given number n
function fact($n)
{
    $f = 1;
    for ($i = 2; $i <= $n; $i++)
        $f *= $i;
    return $f;
}

// Driver Code

// Number of values given
$n = 4;
$x = array( 45, 50, 55, 60 );

// y[,] is used for difference table
// with y[,0] used for input
$y = array_fill(0, $n,
     array_fill(0, $n, 0));
$y[0][0] = 0.7071;
$y[1][0] = 0.7660;
$y[2][0] = 0.8192;
$y[3][0] = 0.8660;

// Calculating the forward difference
// table
for ($i = 1; $i < $n; $i++)
{
    for ($j = 0; $j < $n - $i; $j++)
        $y[$j][$i] = $y[$j + 1][$i - 1] -
                     $y[$j][$i - 1];
}

// Displaying the forward difference table
for ($i = 0; $i < $n; $i++)
{
    print($x[$i] . "\t");
    for ($j = 0; $j < $n - $i; $j++)
        print($y[$i][$j] . "\t");
    print("\n");
}

// Value to interpolate at
$value = 52;

// initializing u and sum
$sum = $y[0][0];
$u = ($value - $x[0]) / ($x[1] - $x[0]);
for ($i = 1; $i < $n; $i++)
{
    $sum = $sum + (u_cal($u, $i) * $y[0][$i]) /
                                    fact($i);
}

print("\nValue at " . $value .
      " is " . round($sum, 6));

// This code is contributed by mits

Javascript

<script>
    // javascript Program to interpolate using
    // newton forward interpolation
    // calculating u mentioned in the formula

    function u_cal(u , n)
    {
        var temp = u;
        for (var i = 1; i < n; i++)
            temp = temp * (u - i);
        return temp;
    }

    // calculating factorial of given number n
    function fact(n)
    {
        var f = 1;
        for (var i = 2; i <= n; i++)
            f *= i;
        return f;
    }
    // Number of values given
    var n = 4;
    var x = [ 45, 50, 55, 60 ];

    // y is used for difference table
    // with y[0] used for input
    var y=Array(n).fill(0.0).map(x => Array(n).fill(0.0));
    y[0][0] = 0.7071;
    y[1][0] = 0.7660;
    y[2][0] = 0.8192;
    y[3][0] = 0.8660;

    // Calculating the forward difference
    // table
    for (var i = 1; i < n; i++) {
        for (var j = 0; j < n - i; j++)
            y[j][i] = y[j + 1][i - 1] - y[j][i - 1];
    }

    // Displaying the forward difference table
    for (var i = 0; i < n; i++) {
        document.write(x[i].toFixed(6)+"    ");
        for (var j = 0; j < n - i; j++)
            document.write(y[i][j].toFixed(6)+"    ");
        document.write('<br>');
    }

    // Value to interpolate at
    var value = 52;

    // initializing u and sum
    var sum = y[0][0];
    var u = (value - x[0]) / (x[1] - x[0]);
    for (var i = 1; i < n; i++) {
        sum = sum + (u_cal(u, i) * y[0][i]) /
                                fact(i);
    }

    document.write("\n Value at "+value.toFixed(6)+" is "+sum.toFixed(6));



// This code is contributed by 29AjayKumar
</script>

Output:

  45    0.7071    0.0589    -0.00569999    -0.000699997    
  50    0.766    0.0532    -0.00639999    
  55    0.8192    0.0468    
  60    0.866    

Value at 52 is 0.788003

Time Complexity: O(n^2) since there are two nested loops to fill the forward difference table and an additional loop to calculate the interpolated value.

Space Complexity: O(n^2), as the forward difference table is stored in a two-dimensional array with n rows and n columns.

Backward Differences: The differences y1 – y0, y2 – y1, ……, yn – yn–1 when denoted by dy1, dy2, ……, dyn, respectively, are called first backward difference. Thus, the first backward differences are : 

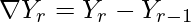
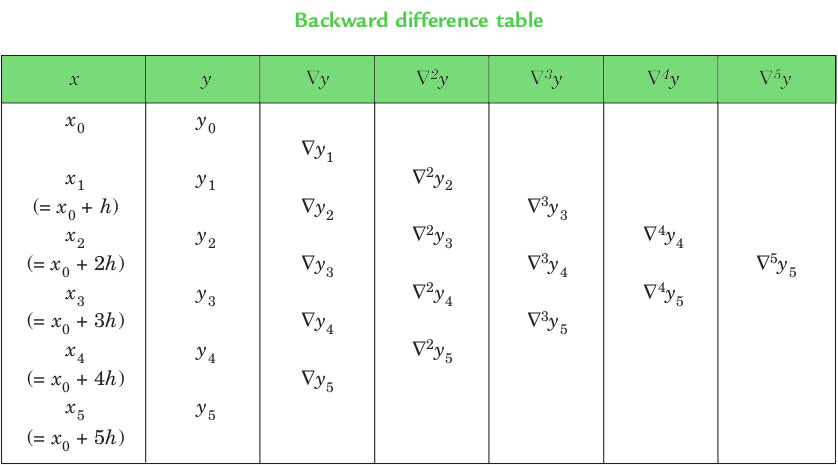
NEWTON’S GREGORY BACKWARD INTERPOLATION FORMULA : 

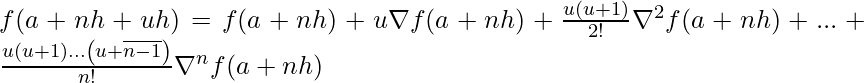
This formula is useful when the value of f(x) is required near the end of the table. h is called the interval of difference and u = ( x – an ) / h, Here an is last term.

Example :  

Input : Population in 1925

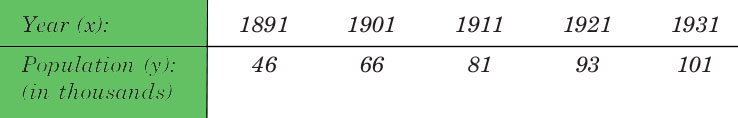
Output :

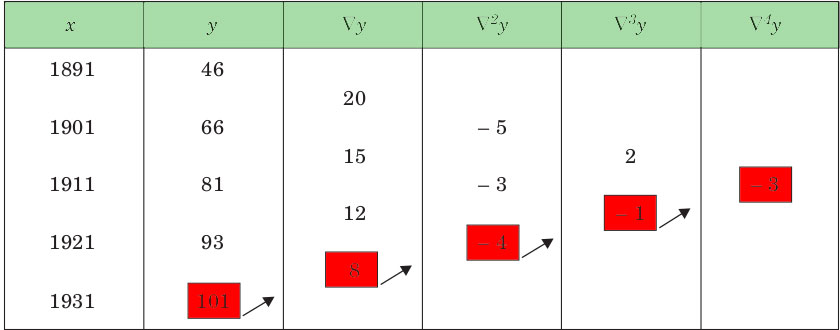
Value in 1925 is 96.8368 

Below is the implementation of the Newton backward interpolation method.  

C++

// CPP Program to interpolate using
// newton backward interpolation
#include <bits/stdc++.h>
using namespace std;

// Calculation of u mentioned in formula
float u_cal(float u, int n)
{
    float temp = u;
    for (int i = 1; i < n; i++)
        temp = temp * (u + i);
    return temp;
}

// Calculating factorial of given n
int fact(int n)
{
    int f = 1;
    for (int i = 2; i <= n; i++)
        f *= i;
    return f;
}

int main()
{
    // number of values given
    int n = 5;
    float x[] = { 1891, 1901, 1911,
                  1921, 1931 };

    // y[][] is used for difference
    // table and y[][0] used for input
    float y[n][n];
    y[0][0] = 46;
    y[1][0] = 66;
    y[2][0] = 81;
    y[3][0] = 93;
    y[4][0] = 101;

    // Calculating the backward difference table
    for (int i = 1; i < n; i++) {
        for (int j = n - 1; j >= i; j--)
            y[j][i] = y[j][i - 1] - y[j - 1][i - 1];
    }

    // Displaying the backward difference table
    for (int i = 0; i < n; i++) {
        for (int j = 0; j <= i; j++)
            cout << setw(4) << y[i][j]
                 << "\t";
        cout << endl;
    }

    // Value to interpolate at
    float value = 1925;

    // Initializing u and sum
    float sum = y[n - 1][0];
    float u = (value - x[n - 1]) / (x[1] - x[0]);
    for (int i = 1; i < n; i++) {
        sum = sum + (u_cal(u, i) * y[n - 1][i]) /
                                     fact(i);
    }

    cout << "\n Value at " << value << " is "
         << sum << endl;
    return 0;
}

Java

// Java Program to interpolate using
// newton backward interpolation
class GFG
{

// Calculation of u mentioned in formula
static double u_cal(double u, int n)
{
    double temp = u;
    for (int i = 1; i < n; i++)
        temp = temp * (u + i);
    return temp;
}

// Calculating factorial of given n
static int fact(int n)
{
    int f = 1;
    for (int i = 2; i <= n; i++)
        f *= i;
    return f;
}

// Driver code
public static void main(String[] args)
{
    // number of values given
    int n = 5;
    double x[] = { 1891, 1901, 1911,
                1921, 1931 };

    // y[][] is used for difference
    // table and y[][0] used for input
    double[][] y = new double[n][n];
    y[0][0] = 46;
    y[1][0] = 66;
    y[2][0] = 81;
    y[3][0] = 93;
    y[4][0] = 101;

    // Calculating the backward difference table
    for (int i = 1; i < n; i++)
    {
        for (int j = n - 1; j >= i; j--)
            y[j][i] = y[j][i - 1] - y[j - 1][i - 1];
    }

    // Displaying the backward difference table
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <= i; j++)
            System.out.print(y[i][j] + "\t");
        System.out.println("");;
    }

    // Value to interpolate at
    double value = 1925;

    // Initializing u and sum
    double sum = y[n - 1][0];
    double u = (value - x[n - 1]) / (x[1] - x[0]);
    for (int i = 1; i < n; i++)
    {
        sum = sum + (u_cal(u, i) * y[n - 1][i]) /
                                    fact(i);
    }
    System.out.println("\n Value at " + value +
                    " is " + String.format("%.6g%n",sum));
}
}

// This code is contributed by mits

Python3

# Python3 Program to interpolate using
# newton backward interpolation

# Calculation of u mentioned in formula
def u_cal(u, n):
    temp = u
    for i in range(n):
        temp = temp * (u + i)
    return temp

# Calculating factorial of given n
def fact(n):
    f = 1
    for i in range(2, n + 1):
        f *= i
    return f


# Driver code


# number of values given
n = 5
x = [1891, 1901, 1911, 1921, 1931]

# y is used for difference
# table and y[0] used for input
y = [[0.0 for _ in range(n)] for __ in range(n)]
y[0][0] = 46
y[1][0] = 66
y[2][0] = 81
y[3][0] = 93
y[4][0] = 101

# Calculating the backward difference table
for i in range(1, n):
    for j in range(n - 1, i - 1, -1):
        y[j][i] = y[j][i - 1] - y[j - 1][i - 1]


# Displaying the backward difference table
for i in range(n):
    for j in range(i + 1):
        print(y[i][j], end="\t")
    print()

# Value to interpolate at
value = 1925

# Initializing u and sum
sum = y[n - 1][0]
u = (value - x[n - 1]) / (x[1] - x[0])
for i in range(1, n):
    sum = sum + (u_cal(u, i) * y[n - 1][i]) / fact(i)

print("\n Value at", value,  "is", sum)


# This code is contributed by phasing17

C#

// C# Program to interpolate using
// newton backward interpolation
using System;

class GFG
{

// Calculation of u mentioned in formula
static double u_cal(double u, int n)
{
    double temp = u;
    for (int i = 1; i < n; i++)
        temp = temp * (u + i);
    return temp;
}

// Calculating factorial of given n
static int fact(int n)
{
    int f = 1;
    for (int i = 2; i <= n; i++)
        f *= i;
    return f;
}

// Driver code
static void Main()
{
    // number of values given
    int n = 5;
    double[] x = { 1891, 1901, 1911,
                1921, 1931 };

    // y[][] is used for difference
    // table and y[][0] used for input
    double[,] y = new double[n,n];
    y[0,0] = 46;
    y[1,0] = 66;
    y[2,0] = 81;
    y[3,0] = 93;
    y[4,0] = 101;

    // Calculating the backward difference table
    for (int i = 1; i < n; i++)
    {
        for (int j = n - 1; j >= i; j--)
            y[j,i] = y[j,i - 1] - y[j - 1,i - 1];
    }

    // Displaying the backward difference table
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <= i; j++)
            Console.Write(y[i,j]+"\t");
        Console.WriteLine("");;
    }

    // Value to interpolate at
    double value = 1925;

    // Initializing u and sum
    double sum = y[n - 1,0];
    double u = (value - x[n - 1]) / (x[1] - x[0]);
    for (int i = 1; i < n; i++)
    {
        sum = sum + (u_cal(u, i) * y[n - 1,i]) /
                                    fact(i);
    }

    Console.WriteLine("\n Value at "+value+" is "+Math.Round(sum,4));
}
}

// This code is contributed by mits

PHP

<?php
// PHP Program to interpolate using
// newton backward interpolation

// Calculation of u mentioned in formula
function u_cal($u, $n)
{
    $temp = $u;
    for ($i = 1; $i < $n; $i++)
        $temp = $temp * ($u + $i);
    return $temp;
}

// Calculating factorial of given n
function fact($n)
{
    $f = 1;
    for ($i = 2; $i <= $n; $i++)
        $f *= $i;
    return $f;
}

// Driver Code

// number of values given
$n = 5;
$x = array(1891, 1901, 1911,
           1921, 1931);

// y[][] is used for difference
// table and y[][0] used for input
$y = array_fill(0, $n, array_fill(0, $n, 0));
$y[0][0] = 46;
$y[1][0] = 66;
$y[2][0] = 81;
$y[3][0] = 93;
$y[4][0] = 101;

// Calculating the backward difference table
for ($i = 1; $i < $n; $i++)
{
    for ($j = $n - 1; $j >= $i; $j--)
        $y[$j][$i] = $y[$j][$i - 1] -
                     $y[$j - 1][$i - 1];
}

// Displaying the backward difference table
for ($i = 0; $i < $n; $i++)
{
    for ($j = 0; $j <= $i; $j++)
        print($y[$i][$j] . "\t");
    print("\n");
}

// Value to interpolate at
$value = 1925;

// Initializing u and sum
$sum = $y[$n - 1][0];
$u = ($value - $x[$n - 1]) / ($x[1] - $x[0]);
for ($i = 1; $i < $n; $i++)
{
    $sum = $sum + (u_cal($u, $i) *
           $y[$n - 1][$i]) / fact($i);
}

print("\n Value at " . $value .
      " is " . round($sum, 4));

// This code is contributed by chandan_jnu
?>

Javascript

<script>
// javascript Program to interpolate using
// newton backward interpolation


// Calculation of u mentioned in formula
function u_cal(u , n)
{
    var temp = u;
    for (var i = 1; i < n; i++)
        temp = temp * (u + i);
    return temp;
}

// Calculating factorial of given n
function fact(n)
{
    var f = 1;
    for (var i = 2; i <= n; i++)
        f *= i;
    return f;
}

// Driver code


    // number of values given
    var n = 5;
    var x = [ 1891, 1901, 1911,
                1921, 1931 ];

    // y is used for difference
    // table and y[0] used for input
    var y = Array(n).fill(0.0).map(x => Array(n).fill(0.0));
    y[0][0] = 46;
    y[1][0] = 66;
    y[2][0] = 81;
    y[3][0] = 93;
    y[4][0] = 101;

    // Calculating the backward difference table
    for (var i = 1; i < n; i++)
    {
        for (var j = n - 1; j >= i; j--)
            y[j][i] = y[j][i - 1] - y[j - 1][i - 1];
    }

    // Displaying the backward difference table
    for (var i = 0; i < n; i++)
    {
        for (var j = 0; j <= i; j++)
            document.write(y[i][j] + "\t");
        document.write('<br>');;
    }

    // Value to interpolate at
    var value = 1925;

    // Initializing u and sum
    var sum = y[n - 1][0];
    var u = (value - x[n - 1]) / (x[1] - x[0]);
    for (var i = 1; i < n; i++)
    {
        sum = sum + (u_cal(u, i) * y[n - 1][i]) /
                                    fact(i);
    }
    document.write("\n Value at " + value +
                    " is " +sum);

// This code is contributed by 29AjayKumar
</script>

Output:

  46    
  66      20    
  81      15      -5    
  93      12      -3       2    
 101       8      -4      -1      -3    

 Value at 1925 is 96.8368

Time Complexity : O(N*N) ,N is the number of rows.

Space Complexity : O(N*N) ,for storing elements in difference table.

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.