Kinetic Molecular Theory of Gases
Last Updated :
02 Dec, 2021
The kinetic molecular theory of gases explains a gas’s three macroscopic characteristics in terms of the microscopic nature of the gas’s atoms and molecules. The size, shape, mass, and volume of solids and liquids are commonly used to characterize their physical properties. Gases, on the other hand, have no definite shape or size, and their mass and volume are not measured directly. The physical properties of each gas can be characterized in terms of three measurable macroscopic properties using the kinetic theory of gases.
Kinetic Molecular Theory of Gases
The kinetic theory of gases is a theoretical model that describes the molecular composition of a gas in terms of a large number of submicroscopic particles like atoms and molecules. The theory also states that gas pressure is caused by particles hitting each other and the container’s walls. Temperature, volume, and pressure are all defined by the kinetic theory of gases, also transport qualities like viscosity and thermal conductivity, as well as mass diffusivity. It essentially explains all of the aspects of the microscopic phenomenon.
The theory is important because it aids in the development of a relationship between macroscopic characteristics and microscopic phenomena. The kinetic theory of gases aids in the understanding of molecular action. In general, gas molecules are always in motion and tend to clash with one another and the container walls. Since its assumptions are based on microscopic particles found in gases, so the kinetic molecular theory is sometimes known as the microscopic model. Bernoulli proposed the idea, which was later explored and expanded by Clausius, Maxwell, Boltzmann, and others.
Postulates of Kinetic Molecular Theory of Gases
The fundamental postulates of the kinetic molecular theory of gases are as follows:
- The kinetic theory of gas postulates is beneficial in deducing macroscopic properties from microscopic properties.
- Gases are made up of a lot of small particles (atoms and molecules). When compared to the distance between the particles, these particles are exceedingly small. Individual particles are regarded as insignificant, and the majority of the volume occupied by the gas is empty space.
- These molecules are in a constant state of random motion, causing them to collide with one another and with the container’s walls. When gas molecules collide with the container’s walls, the molecules give the walls some momentum. Essentially, this results in the generation of a measurable force. So, if we divide this force by the area, the pressure is defined.
- The molecules’ collisions with the walls are fully elastic. That means the molecules do not lose kinetic energy when they collide. Molecules do not slow down and will continue to move at the same rate. During the collisions, however, there may be a redistribution of energy.
- The average kinetic of the gas particles is directly proportional to the absolute temperature. As a result, as the temperature rises, the average kinetic energy of the gas particles decreases. In other words, the higher the temperature, the larger the gas’s average kinetic energy.
- The molecules are separated by a significant amount of space. The empty spaces between the molecules are so large that the actual volume of the molecules in comparison to the total volume of the gas is negligible.
- At ordinary temperature and pressure, there are no forces of interaction (attractive or repulsive) between the molecules. They move in complete isolation from one another.
- The gas exerts pressure due to the collision of its molecules with the container’s walls per unit area.
Gas Laws for Ideal Gases
- Pressure α Number of Particles at Constant Volume: Pressure is created when particles collide with the container’s walls. The greater the number of gas particles, the greater the number of particles colliding with the container’s walls. The larger the amount (or a number of particles) of the gas, at constant temperature and volume, the higher the pressure.
- Avogadro’s Law – At Constant Pressure: N α V. The number of collisions and pressure rise as the number of particles increases. If the pressure remains constant, the only way to reduce the number of collisions is to increase the volume. The volume is proportional to the amount of gas at constant pressure.
- Boyle’s Law (Pressure at Constant Temperature): The kinetic energy of particles remains constant at a constant temperature. The number of particles per unit volume or area increases when the volume is reduced at a constant temperature. The frequency of collisions per unit area increases as the number of particles in the unit area increases. At constant temperature, the greater the pressure, the smaller the container’s volume.
- Amonton’s Law: At Constant Volume: P α T. The particle’s kinetic energy rises as the temperature rises. When the volume remains constant, particles travel quickly, increasing the frequency of collisions per unit time on the container’s walls and, as a result, the pressure. The higher the temperature, the higher the pressure of the gas at constant volume.
- Charles’s Law – At Constant Pressure: V α T. The change in temperature is proportional to the change in pressure. If the pressure must also be kept constant, the number of collisions must be adjusted accordingly. Collisions can only be modified by changing the area or volume at constant pressure and a constant amount of substance. Volume changes proportionally to temperature under constant pressure.
- Graham Law of Diffusion: Graham’s law states that a gas’s rate of diffusion is inversely proportional to its molecular weight squared. At the same temperature, two gases with molecular weights M1 and M2 will have the same kinetic energy. Then,
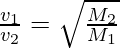
The molecular weights are inversely proportional to the molecules’ velocity.
- Dalton’s Law: The pressure of gas molecules on the container’s walls. The molecules of one gas behave independently of the molecules of other gases in the mixture due to the absence of attraction forces. As a result, no molecule is influenced by others when it collides with the container’s walls. As if the molecules of one gas did not exist, the molecules of the other gas contribute to the total pressure. As a result, the total pressure of a mixture of gases is equal to the sum of their partial pressures. This is known as Dalton’s law.
Non-ideal Gas Behaviour
Only under specific conditions of low pressures and high temperatures do all gas molecules obey the ideal gas laws. The deviations of real gases from ideal gas behaviour can be traced back to improper or incorrect postulate assumptions.
These laws are,
- Since the particles are point charges with no volume, compressing the gases to zero volume should be conceivable. However, the fact that gases cannot be squeezed to zero volume implies that particles, despite their small size, have volume and should not be overlooked.
- Particles are self-contained and do not interact with one another: Particles do interact with one another depending on their nature. The pressure of the gas is affected by the interactions. The volume and interactions differ from one gas to the next. For real gases, a number of gas laws have been devised that include correction factors for pressure and volume.
- Collisions between particles are elastic and energy is exchanged. As a result, the particles do not have the same energy and have an energy distribution.
Maxwell – Boltzmann Molecular Distribution of Molecular Speeds
A gas is made up of thousands of small particles separated by enormous empty gaps. These particles move in all directions at all times. They collide with each other as well as the container’s walls during their motion. The speed and direction of the molecules change as a result of collisions.
So, not all of the molecules in a particular gas sample have the same speed. Individual molecular speeds vary and are spread out over a vast range. Even if all of the particles started out at the same speed, molecular collisions will cause them to diverge. The speeds of certain molecules are likewise constantly altering. At a given temperature, however, the distribution of speeds among various molecules remains constant, even if the individual speeds of the molecules fluctuate.
As a result, the proportion of molecules moving at a specific speed remains constant. Since Maxwell and Boltzmann were the first to formulate it, so this is known as the distribution of speeds and also as the Maxwell-Boltzmann distribution law. The kinetic theory of gases predicts that particles are continually in motion and that their kinetic energy is proportional to the gas’s temperature. Maxwell – Boltzmann used this theory to determine the distribution of gaseous particles between energy zero and infinity, as well as the most common, average, and root mean square velocity of the particles.
Sample Questions
Question 1: What is the kinetic theory’s main foundation?
Answer:
The kinetic theory of gases explains how gases behave by assuming that they are made up of quickly moving atoms or molecules.
Question 2: Define the kinetic gas equation.
Answer:
An equation for the pressure of the gas was derived using the postulates of kinetic molecular theory. The kinetic gas equation is the name for this equation. It’s written as,
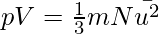
where m is the molecule’s mass, N is the volume’s number of molecules, and u is the velocity.
Question 3: Why are vegetables harder to cook in hill stations?
Answer:
Since the atmospheric pressure is lower in hill stations, so the boiling point is also lower and it becomes harder to cook in hill stations.
Question 4: What are the kinetic model’s three main points?
Answer:
The most basic kinetic model is based on the following assumptions.
- The gas is made up of a large number of identical molecules moving in random directions, separated by large distances compared to their size.
- The molecules collide completely elastically (with no energy loss) with each other and with the container walls, but otherwise do not interact.
- Kinetic energy is transferred between molecules through heat.
Question 5: Explain why -2730C is the lowest temperature according to Charle’s law.
Answer:
Under constant pressure, volume changes proportionally to temperature, according to Charle’s law. At -2730C, the volume of the gas equals zero, indicating that the gas no longer exists. As a result, the lowest temperature is -273 0C.
Share your thoughts in the comments
Please Login to comment...