Jacobian matrix in PyTorch
Last Updated :
15 Jul, 2021
Introduction:
The Jacobian is a very powerful operator used to calculate the partial derivatives of a given function with respect to its constituent latent variables. For refresher purposes, the Jacobian of a given function 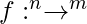 with respect to a vector
with respect to a vector 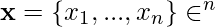 is defined as
is defined as
![Rendered by QuickLaTeX.com \mathbf{J}_f(\mathbf{x}) = \begin{bmatrix} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2} & \ldots & \frac{\partial f}{\partial x_n}\end{bmatrix}= \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \ldots & \frac{\partial f_1}{\partial x_n} \\[1ex] \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \ldots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3082ad5fd089644599ce142deb87b0cc_l3.png)
Example:
Suppose we have a vector ![Rendered by QuickLaTeX.com \mathbf{x} = \begin{bmatrix} x_{1} \\[1ex]x_{2} \\[1ex]x_{3} \end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e4732acccba22d0addf5978743e63195_l3.png) and a function
and a function ![Rendered by QuickLaTeX.com f(\mathbf{x}) = f(x_1,x_2,x_3)= \begin{bmatrix}f_{1} \\[1ex]f_{2}\\[1ex]f_{3}\end{bmatrix} = \begin{bmatrix}x_1+x_2 \\[1ex]x_1 \times x_3 \\[1ex]x_2^{3}\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-667c64a4ec5ac0be5c590ef7889e8707_l3.png) . To calculate the Jacobian of
. To calculate the Jacobian of 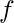 with respect to
with respect to  , we can use the above-mentioned formula to get
, we can use the above-mentioned formula to get
![Rendered by QuickLaTeX.com \mathbf{J}_f(\mathbf{x}) = \begin{bmatrix} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2} & \frac{\partial f}{\partial x_3}\end{bmatrix}= \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \frac{\partial f_1}{\partial x_3} \\[1ex] \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \frac{\partial f_2}{\partial x_3} \\[1ex] \frac{\partial f_3}{\partial x_1} & \frac{\partial f_3}{\partial x_2} & \frac{\partial f_3}{\partial x_3} \end{bmatrix}=\begin{bmatrix} \frac{\partial (x_1 + x_2)}{\partial x_1} & \frac{\partial (x_1 + x_2)}{\partial x_2} & \frac{\partial (x_1 + x_2)}{\partial x_3} \\[1ex] \frac{\partial (x_1 \times x_3)}{\partial x_1} & \frac{\partial (x_1 \times x_3)}{\partial x_2} & \frac{\partial (x_1 \times x_3)}{\partial x_3} \\[1ex] \frac{\partial x_2^3}{\partial x_1} & \frac{\partial x_2^3}{\partial x_2} & \frac{\partial x_2^3}{\partial x_3} \end{bmatrix} = \begin{bmatrix}1 & 1 & 0 \\[1ex] x_3 & 0 & x_1 \\[1ex] 0 & 3\times x_2^2&0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68c85a2508034a538afdc4290f3fbe54_l3.png)
To achieve the same functionality as above, we can use the jacobian() function from Pytorch’s torch.autograd.functional utility to compute the Jacobian matrix of a given function for some inputs.
Syntax: torch.autograd.functional.jacobian(func, inputs, create_graph=False, strict=False, vectorize=False)
Parameters:
- func: A Python function which takes input and outputs a Pytorch Tensor(or a tuple of Tensors).
- inputs: The inputs are passed as parameters to the ‘func’ method. The input can be a single Pytorch Tensor(or a tuple of Tensors)
- create_graph: If True, the autograd engine creates a backpropable graph for doing further operations on gradients. Defaults to False.
- strict: If True, an error will be raised when the engine detects that there exists an input such that all the outputs are independent of it. If False, returns zero gradients for such inputs. Defaults to False.
- vectorize: Still in it’s experimental phase if True, the function uses the vmap prototype feature to compute the gradients by only one call of the autograd engine instead of one call per each row of the matrix. Defaults to False.
Installation:
For this article, you only need the torch utility, which can be downloaded through the pip package manager using:
pip install torch
Example usage of the function:
We’ll be using the same function and vector for ease of flow, as discussed in the above example. Since tensors are the basic building blocks of the Pytorch package, we’ll be using them for representing both the inputs vectors and the given function. This article assumes a basic familiarity with Pytorch tensors which can be quickly reviewed by going through Pytorch articles.
Theoretical verification:
Suppose we have a vector ![Rendered by QuickLaTeX.com \mathbf{x} = \begin{bmatrix} x_{1} \\[1ex]x_{2} \\[1ex]x_{3} \end{bmatrix} = \begin{bmatrix} 3 \\[1ex]4 \\[1ex]5 \end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bad6c3f8e26b58dedf1ccd5e875fd0a7_l3.png) as a given input. By plugging in the values of
as a given input. By plugging in the values of  into the above derived equation we will get
into the above derived equation we will get ![Rendered by QuickLaTeX.com J_f({\mathbf{x}}) =\begin{bmatrix}1 & 1 & 0 \\[1ex] x_3 & 0 & x_1 \\[1ex] 0 & 3\times x_2^2&0\end{bmatrix}=\begin{bmatrix}1 & 1 & 0 \\[1ex] 5 & 0 & 3 \\[1ex] 0 & 3\times 4^2&0\end{bmatrix}= \begin{bmatrix}1 & 1 & 0 \\[1ex] 5 & 0 & 3 \\[1ex] 0 & 48 & 0\end{bmatrix}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9ef325e54cad38e5ff4eb4e4f436d6f3_l3.png)
Code: Python implementation to show the working of Jacobian Matrix using Pytorch
Python
from torch.autograd.functional import jacobian
from torch import tensor
def f(x1,x2,x3):
return (x1 + x2, x3*x1, x2**3)
x1 = tensor(3.0)
x2 = tensor(4.0)
x3 = tensor(5.0)
print(jacobian(f,(x1,x2,x3)))
|
Output:
((tensor(1.), tensor(1.), tensor(0.)),
(tensor(5.), tensor(0.), tensor(3.)),
(tensor(0.), tensor(48.), tensor(0.)))
The output is exactly similar to our theoretical verification! Using a similar approach, we can calculate the Jacobian matrix of any given function using the Pytorch API.
References:
- https://pytorch.org/docs/stable/autograd.html#torch.autograd.functional.jacobian
- https://pytorch.org/docs/stable/tensors.html
Share your thoughts in the comments
Please Login to comment...