Jacobian and Hessian Matrices beyond Gradients

Sometimes we need to find all of the partial derivatives of a function with both vector input and output. A Jacobian matrix is a matrix that contains all of these partial derivatives. In particular, if we have a function 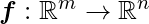, the Jacobian matrix  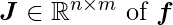is defined as .

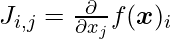We’re sometimes intrigued by a derivative of a derivative which is called a second derivative. The derivative of f: \mathbb{R}^{n} \rightarrow \mathbb{R}    with respect to x_{i}    of the derivative of f    with respect to x_{j}    is represented as \frac{\partial^{2}}{\partial x_{i} \partial x_{j}} f   . We can denote \frac{d^{2}}{d x^{2}} f \text { by } f^{\prime \prime}(x)    in a single dimension. The second derivative shows how the first derivative changes as the input changes. This is significant because it tells us if a gradient step will result in as much improvement as the gradient alone would suggest. The second derivative can be thought of as a measurement of curvature. Consider the case of a quadratic function (many functions that arise in practice are not quadratic but can be approximated well as quadratic, at least locally). There is no curvature if the second derivative of such a function is 0. It’s a completely flat line, and the gradient alone can forecast its value. If the gradient is 1, we can take a size step \epsilon   along the negative gradient to reduce the cost function by \epsilon   . Because the function curves downward when the second derivative is negative, the cost function will actually fall by more than \epsilon   . Finally, if the second derivative is positive, the function bends upward, allowing for a cost function drop of less than \epsilon   .

There are many second derivatives when our function has several input dimensions. These derivatives can be gathered into a matrix known as the Hessian matrix. 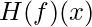 is a Hessian matrix defined as follows:

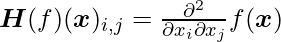
In other words, the Hessian is the gradient’s Jacobian. The differential operators are commutative anywhere the second partial derivatives are continuous, i.e. their order can be swapped:

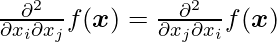
As a result, 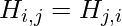 implying that the Hessian matrix is symmetric at these places. Almost all of the functions we come across in the area of deep learning have a symmetric Hessian. We can partition the Hessian matrix into a set of real eigenvalues and an orthogonal basis of eigenvectors because it is real and symmetric.  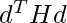is the second derivative in a particular direction represented by a unit vector 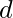. The second derivative in that direction is supplied by the corresponding eigenvalue when  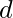is an eigenvector of 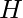. The directional second derivative in other directions of  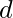is a weighted average of all of the eigenvalues, with weights ranging from 0 to 1, with eigenvectors having smaller angles with  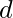receiving greater weight. The maximum second derivative is determined by the largest eigenvalue, while the minimum second derivative is determined by the smallest eigenvalue.

The (directional) second derivative indicates how well a gradient descent step is likely to execute. Around the present point 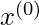, we can approximate the function  with a second-order Taylor series:

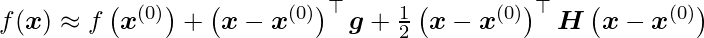
where 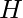 is the Hessian at  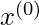and 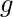 is the gradient. If we apply a learning rate  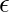of, then  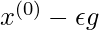will give us the new point 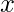. When we plug this into our approximation, we get

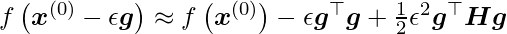
There are three terms here: the function’s original value, the expected improvement owing to the slope, and the correction we must apply to account for the function’s curvature. The gradient descending step can actually travel uphill if this last term is too large. The Taylor series approximation predicts that growing forever will reduce f forever when 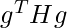 is zero or negative. In practice, the Taylor series is unlikely to remain accurate for large, hence heuristic choices of 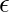are required in this instance. When  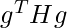is positive, finding the smallest step size that minimizes the Taylor series approximation of the function yields

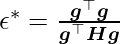
When 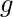 aligns with the eigenvector of H corresponding to the maximal eigenvalue 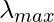, the best step size is  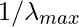in the worst situation. The eigenvalues of the Hessian define the size of the learning rate to the degree that the function we minimize can be approximated well by a quadratic function. A crucial point can be classified as a local maximum, local minimum, or saddle point using the second derivative. Remember that  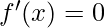at a critical point. The first derivative  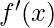grows as we move to the right and drops as we move to the left when the second derivative . 

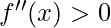For small enough 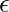, this means 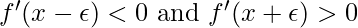. In other words, the slope begins to point uphill to the right as we travel right, and the slope begins to point uphill to the left as we move left. We can deduce that  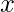is a local minimum when  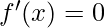and 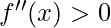. Similarly, we can deduce that  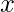is a local maximum when  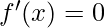and 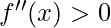. This is a second derivative test. Unfortunately, the test is inconclusive when 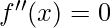.  could be a saddle point or a flat zone in this example.

In several dimensions, we must investigate all of the function’s second derivatives. We may generalize the second derivative test to several dimensions by using the eigendecomposition of the Hessian matrix. We can study the eigenvalues of the Hessian at a critical point when 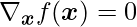 to identify whether the critical point is a local maximum, local minimum, or saddle point. The point is a local minimum when the Hessian is positive definite (all of its eigenvalues are positive). This can be observed by noting that the directional second derivative must be positive in any direction and referring to the univariate second derivative test. The point is also a local maximum when the Hessian is negative definite (all of its eigenvalues are negative). It is feasible to establish positive proof of saddle points in many dimensions in some circumstances. We know that  is a local maximum on one cross-section of 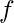 but a local minimum on another cross-section when at least one eigenvalue is positive and at least one eigenvalue is negative. Finally, like the univariate version, the multidimensional second derivative test can be inconclusive. When all of the non-zero eigenvalues have the same sign but at least one is zero, the test is inconclusive. This is because in the cross-section corresponding to the zero eigenvalues, the univariate second derivative test is unconvincing.

At a single location in multiple dimensions, each direction has a separate second derivative. The Hessian’s condition number at this point indicates how far the second derivatives diverge from one another. Gradient descent performs badly when the Hessian has a low condition number. This is due to the fact that the derivative increases swiftly in one direction but slowly in the other. Gradient descent is uninformed of this change in the derivative, hence it is unaware that it should preferentially explore in the direction where the derivative remains negative for a longer period of time. It also makes selecting a suitable step size challenging. The step size must be small enough to avoid traveling uphill in directions with strong positive curvature and overshooting the minimum. This usually indicates that the step size is too tiny to make substantial progress in less curvy routes.

This problem can be solved by guiding the search with information from the Hessian matrix. Newton’s approach is the most basic method for doing so. Newton’s technique is based on approximating  near  via a second-order Taylor series expansion:

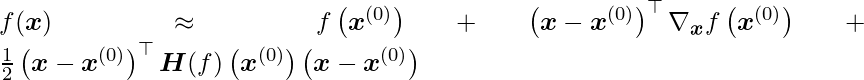
The critical point of this function is found by solving for it:

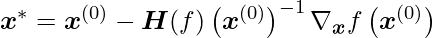
Newton’s method consists of using the above equation once to leap to the function’s minimum directly when 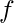 is a positive definite quadratic function. Newton’s method consists of using the above equation numerous times when  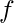is not actually quadratic but can be locally approximated as a positive definite quadratic. Leaping to the approximation’s minimum and iteratively updating the approximation can quickly get the critical point as compared to gradient descent. This is an advantageous attribute near a local minimum, but it might be detrimental near a saddle point. Newton’s approach is only appropriate when the nearest critical point is a minimum (all the Hessian eigenvalues are positive), whereas gradient descent is not attracted to saddle points until the gradient points toward them.

First-order optimization algorithms – Optimization algorithms that use only the gradient, such as gradient descent. Optimization algorithms that also use the Hessian matrix, such as Newton’s method, are called second-order optimization algorithms.

Although the optimization procedures used throughout this book are applicable to a wide range of functions, they come with few guarantees. Because the family of functions employed in deep learning is highly complicated, deep learning algorithms often lack guarantees. The prevalent approach to optimization in many other domains is to create optimization algorithms for a small set of functions. In the context of deep learning, restricting ourselves to functions that are Lipschitz continuous or have Lipschitz continuous derivatives can provide certain guarantees. The rate of change of a Lipschitz continuous function f is bounded by the Lipschitz constant L:

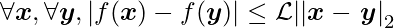
This attribute is useful because it quantifies our assumption that a minor change in the input by a gradient descent algorithm would result in a small change in the output. Lipschitz continuity is also a relatively weak restriction, and many deep learning optimization problems can be made Lipschitz continuous with only small changes.

Convex optimization is perhaps the most successful discipline of specialized optimization. Stronger constraints allow convex optimization methods to provide many more guarantees. Only convex functions—functions for which the Hessian is positive semidefinite everywhere—are suitable for convex optimization techniques. Because such functions lack saddle points and all of their local minima must be global minima, they are well-behaved. The majority of deep learning problems, however, are difficult to characterize in terms of convex optimization. Only a few deep learning techniques use convex optimization as a subroutine. Convex optimization strategies can provide inspiration for showing the convergence of deep learning systems. In the context of deep learning, however, the value of convex optimization is drastically lessened.