Iterative Fast Fourier Transformation for polynomial multiplication
Last Updated :
04 Apr, 2023
Given two polynomials, A(x) and B(x), find the product C(x) = A(x)*B(x). In the previous post, we discussed the recursive approach to solve this problem which has O(nlogn) complexity.
Examples:
Input :
A[] = {9, -10, 7, 6}
B[] = {-5, 4, 0, -2}
Output :
C(x) = 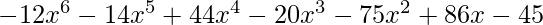
In real-life applications such as signal processing, speed matters a lot, this article examines an efficient FFT implementation. This article focuses on the iterative version of the FFT algorithm that runs in O(nlogn) time but can have a lower constant hidden than the recursive version plus it saves the recursion stack space.
Pre-requisite: recursive algorithm of FFT.
Recall the recursive-FFT pseudo code from previous post, in the for loop evaluation of 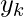 ,
, 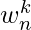 is calculated twice. We can change the loop to compute it only once, storing it in a temporary variable t. So, it becomes,
is calculated twice. We can change the loop to compute it only once, storing it in a temporary variable t. So, it becomes,
for k 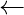 0 to n/2 – 1
0 to n/2 – 1
do t![Rendered by QuickLaTeX.com \leftarrow \omega y^{\left [ 1 \right ]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d9306d825518f1bb18bf1444f96a6591_l3.png)
![Rendered by QuickLaTeX.com y_{k}\leftarrow \omega y_{k}^{\left [ 0 \right ]} + t](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e266b7db288415e0866da4c702c3aff_l3.png)
![Rendered by QuickLaTeX.com y_{k + \left ( n/2 \right )}\leftarrow _{k}^{\left [ 0 \right ]} - t](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e21bdb4694245080340a97a6740191ce_l3.png)
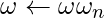
The operation in this loop, multiplying the twiddle factor w = 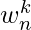 by
by ![Rendered by QuickLaTeX.com y_k^[^1^]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78ac059bffeeee82ff53be7a4c7e7562_l3.png) , storing the product into t, and adding and subtracting t from
, storing the product into t, and adding and subtracting t from ![Rendered by QuickLaTeX.com y_k^[^0^]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3655599e5823d56b5f3f7bb0129f66fa_l3.png) , is known as a butterfly operation.
, is known as a butterfly operation.
Pictorially, this is what a butterfly operation looks like:

Let us take for n=8 and proceed with the formation of the iterative FFT algorithm. Looking at the recursion tree above, we find that if we arrange the elements of the initial coefficient vector into the order in which they appear in the leaves, we could trace the execution of the Recursive-FFT procedure, but bottom-up instead of top-down. First, we take the elements in pairs, compute the DFT of each pair using one butterfly operation, and replace the pair with its DFT. The vector then holds n/2 2-element DFTs. Next, we take these n/2 DFTs in pairs and compute the DFT of the four-vector elements they come from by executing two butterfly operations, replacing two 2-element DFTs with one 4-element DFT. The vector then holds n/4 4-element DFTs. We continue in this manner until the vector holds two (n/2) element DFTs, which we combine using n/2 butterfly operations into the final n-element DFT.

To turn this bottom-up approach into code, we use an array A[0…n] that initially holds the elements of the input vector a in the order in which they appear in the leaves of the tree. Because we have to combine DFT so n each level of the tree, we introduce a variable s to count the levels, ranging from 1 (at the bottom, when we are combining pairs to form 2-element DFTs) to lgn (at the top, when we are combining two n/2 element DFTs to produce the final result). The algorithm therefore is:
1. for s=1 to lgn
2. do for k=0 to n-1 by 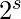 3. do combine the two
3. do combine the two 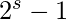 -element DFTs in A[k...k+
-element DFTs in A[k...k+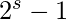 -1] and A[k+
-1] and A[k+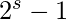 ...k+
...k+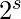 -1] into one 2s-element DFT in A[k...k+
-1] into one 2s-element DFT in A[k...k+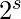 -1]
-1]
Now for generating the code, we arrange the coefficient vector elements in the order of leaves. Example- The order in leaves 0, 4, 2, 6, 1, 5, 3, 7 is a bit reversal of the indices. Start with 000, 001, 010, 011, 100, 101, 110, 111 and reverse the bits of each binary number to obtain 000, 100, 010, 110, 001, 101, 011, 111.Pseudocode for iterative FFT :
BIT-REVERSE-COPY(a, A)
n = length [a]
for k = 0 to n-1
do A[rev(k)] = a[k]
ITERATIVE-FFT
BIT-REVERSE-COPY(a, A)
n = length(a)
for s = 1 to log n
do m= 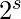
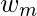 =
= 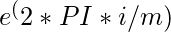 for j = 0 to m/2-1 do for k = j to n-1 by m do t =
for j = 0 to m/2-1 do for k = j to n-1 by m do t = 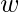 A[k+m/2] u = A[k] A[k] = u+t A[k+m/2] = u-t
A[k+m/2] u = A[k] A[k] = u+t A[k+m/2] = u-t 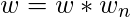 return A
return A
It will be more clear from the below parallel FFT circuit :

CPP
#include <bits/stdc++.h>
using namespace std;
typedef complex<double> cd;
const double PI = 3.1415926536;
unsigned int bitReverse(unsigned int x, int log2n)
{
int n = 0;
for (int i = 0; i < log2n; i++) {
n <<= 1;
n |= (x & 1);
x >>= 1;
}
return n;
}
void fft(vector<cd>& a, vector<cd>& A, int log2n)
{
int n = 4;
for (unsigned int i = 0; i < n; ++i) {
int rev = bitReverse(i, log2n);
A[i] = a[rev];
}
const complex<double> J(0, 1);
for (int s = 1; s <= log2n; ++s) {
int m = 1 << s;
int m2 = m >> 1;
cd w(1, 0);
cd wm = exp(J * (PI / m2));
for (int j = 0; j < m2; ++j) {
for (int k = j; k < n; k += m) {
cd t = w * A[k + m2];
cd u = A[k];
A[k] = u + t;
A[k + m2] = u - t;
}
w *= wm;
}
}
}
int main()
{
vector<cd> a{ 1, 2, 3, 4 };
vector<cd> A(4);
fft(a, A, 2);
for (int i = 0; i < 4; ++i)
cout << A[i] << "\n";
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
import java.util.stream.*;
public class Main {
static class Complex {
double real, imag;
public Complex(double r, double i)
{
real = r;
imag = i;
}
public Complex() { this(0, 0); }
public Complex add(Complex b)
{
return new Complex(real + b.real,
imag + b.imag);
}
public Complex subtract(Complex b)
{
return new Complex(real - b.real,
imag - b.imag);
}
public Complex multiply(Complex b)
{
return new Complex(
real * b.real - imag * b.imag,
real * b.imag + imag * b.real);
}
public String toString()
{
return "(" + real + ", " + imag + ")";
}
}
static int bitReverse(int x, int log2n)
{
int n = 0;
for (int i = 0; i < log2n; i++) {
n <<= 1;
n |= (x & 1);
x >>= 1;
}
return n;
}
static void fft(List<Complex> a, List<Complex> A,
int log2n)
{
int n = 1 << log2n;
for (int i = 0; i < n; ++i) {
int rev = bitReverse(i, log2n);
A.set(i, a.get(rev));
}
final Complex J = new Complex(0, 1);
for (int s = 1; s <= log2n; ++s) {
int m = 1 << s;
int m2 = m >> 1;
Complex w = new Complex(1, 0);
Complex wm
= new Complex(Math.cos(Math.PI / m2),
Math.sin(Math.PI / m2));
for (int j = 0; j < m2; ++j) {
for (int k = j; k < n; k += m) {
Complex t = w.multiply(A.get(k + m2));
Complex u = A.get(k);
A.set(k, u.add(t));
A.set(k + m2, u.subtract(t));
}
w = w.multiply(wm);
}
}
}
public static void main(String[] args)
{
List<Complex> a = Arrays.asList(
new Complex(1, 0), new Complex(2, 0),
new Complex(3, 0), new Complex(4, 0));
List<Complex> A = new ArrayList<>(
Arrays.asList(new Complex[4]));
fft(a, A, 2);
for (int i = 0; i < 4; ++i)
System.out.println(A.get(i));
}
}
|
Python3
import cmath
def bitReverse(x, log2n):
n = 0
for i in range(log2n):
n <<= 1
n |= (x & 1)
x >>= 1
return n
def fft(a, A, log2n):
n = 4
for i in range(n):
rev = bitReverse(i, log2n)
A[i] = a[rev]
J = complex(0, 1)
for s in range(1, log2n + 1):
m = 1 << s
m2 = m >> 1
w = complex(1, 0)
wm = cmath.exp(J * (cmath.pi / m2))
for j in range(m2):
for k in range(j, n, m):
t = w * A[k + m2]
u = A[k]
A[k] = u + t
A[k + m2] = u - t
w *= wm
a = [1, 2, 3, 4]
A = [0, 0, 0, 0]
fft(a, A, 2)
for i in range(4):
print(A[i])
|
Javascript
class Complex {
constructor(r, i){
this.real = r;
this.imag = i;
}
add(b) {
return new Complex(this.real + b.real, this.imag + b.imag);
}
subtract(b) {
return new Complex(this.real - b.real, this.imag - b.imag);
}
multiply(b) {
return new Complex(this.real * b.real - this.imag * b.imag, this.real * b.imag + this.imag * b.real);
}
toString() {
return "(" + this.real + ", " + this.imag + ")";
}
}
function bitReverse(x, log2n) {
let n = 0;
for (let i = 0; i < log2n; i++) {
n <<= 1;
n |= (x & 1);
x >>= 1;
}
return n;
}
function fft(a, A, log2n) {
let n = 1 << log2n;
for (let i = 0; i < n; ++i) {
let rev = bitReverse(i, log2n);
A[i] = a[rev];
}
const J = new Complex(0, 1);
for (let s = 1; s <= log2n; ++s) {
let m = 1 << s;
let m2 = m >> 1;
let w = new Complex(1, 0);
let wm = new Complex(Math.cos(Math.PI / m2), Math.sin(Math.PI / m2));
for (let j = 0; j < m2; ++j) {
for (let k = j; k < n; k += m) {
let t = w.multiply(A[k + m2]);
let u = A[k];
A[k] = u.add(t);
A[k + m2] = u.subtract(t);
}
w = w.multiply(wm);
}
}
}
let a = new Array(4);
a[0] = new Complex(1, 0);
a[1] = new Complex(2, 0);
a[2] = new Complex(3, 0);
a[3] = new Complex(4, 0);
let A = new Array(4);
for(let i = 0; i < 4; i++){
A[i] = new Complex(0, 0);
}
fft(a, A, 2);
for (let i = 0; i < 4; ++i)
console.log("(" + Math.floor(A[i].real) + "," + A[i].imag + ")");
|
C#
using System;
using System.Collections.Generic;
class MainClass {
public class Complex {
public double real, imag;
public Complex(double r, double i)
{
real = r;
imag = i;
}
public Complex()
{
this.real = 0;
this.imag = 0;
}
public Complex add(Complex b)
{
return new Complex(real + b.real,
imag + b.imag);
}
public Complex subtract(Complex b)
{
return new Complex(real - b.real,
imag - b.imag);
}
public Complex multiply(Complex b)
{
return new Complex(
real * b.real - imag * b.imag,
real * b.imag + imag * b.real);
}
public override string ToString()
{
return "(" + real + ", " + imag + ")";
}
}
static int bitReverse(int x, int log2n)
{
int n = 0;
for (int i = 0; i < log2n; i++) {
n <<= 1;
n |= (x & 1);
x >>= 1;
}
return n;
}
static void fft(List<Complex> a, List<Complex> A,
int log2n)
{
int n = 1 << log2n;
for (int i = 0; i < n; ++i) {
int rev = bitReverse(i, log2n);
A[i] = a[rev];
}
Complex J = new Complex(0, 1);
for (int s = 1; s <= log2n; ++s) {
int m = 1 << s;
int m2 = m >> 1;
Complex w = new Complex(1, 0);
Complex wm
= new Complex(Math.Cos(Math.PI / m2),
Math.Sin(Math.PI / m2));
for (int j = 0; j < m2; ++j) {
for (int k = j; k < n; k += m) {
Complex t = w.multiply(A[k + m2]);
Complex u = A[k];
A[k] = u.add(t);
A[k + m2] = u.subtract(t);
}
w = w.multiply(wm);
}
}
}
public static void Main()
{
List<Complex> a = new List<Complex>();
a.Add(new Complex(1, 0));
a.Add(new Complex(2, 0));
a.Add(new Complex(3, 0));
a.Add(new Complex(4, 0));
List<Complex> A = new List<Complex>(new Complex[4]);
fft(a, A, 2);
for (int i = 0; i < 4; ++i)
Console.WriteLine(A[i]);
}
}
|
Input: 1 2 3 4
Output:
(10, 0)
(-2, -2)
(-2, 0)
(-2, 2)
Time complexity Analysis:
The complexity is O(nlgn). To show this we show the innermost loop runs in O(nlgn) time as :
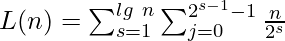
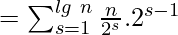
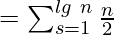
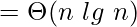
Share your thoughts in the comments
Please Login to comment...