Exponential Squaring (Fast Modulo Multiplication)

Difficulty Level : Medium
Last Updated : 07 Feb, 2020

Given two numbers base and exp, we need to compute base^exp under Modulo 10^9+7

Examples:

Input : base = 2, exp = 2
Output : 4

Input  : base = 5, exp = 100000
Output : 754573817

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

In competitions, for calculating large powers of a number we are given a modulus value(a large prime number) because as the values of 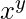$x^y$ is being calculated it can get very large so instead we have to calculate ( 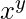$x^y$ %modulus value.)
We can use the modulus in our naive way by using modulus on all the intermediate steps and take modulus at the end,
but in competitions it will definitely show TLE. So, what we can do.
The answer is we can try exponentiation by squaring which is a fast method for calculating exponentiation of a number.
Here we will be discussing two most common/important methods:

Basic Method(Binary Exponentiation)
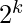$2^k$ -ary method.

Binary Exponentiation

As described in this article we will be using following formula to recursively calculate (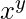 $x^y$ %modulus value):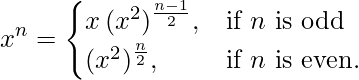

$x^{n}={\begin{cases}x\,(x^{2})^{\frac {n-1}{2}},&{\mbox{if }}n{\mbox{ is odd}}\\(x^{2})^{\frac {n}{2}},&{\mbox{if }}n{\mbox{ is even}}.\end{cases}}$

C++

// C++ program to compute exponential  
// value under modulo using binary  
// exponentiation. 
#include<iostream> 
using namespace std; 
  
#define N 1000000007 // prime modulo value 
  
long int exponentiation(long int base, 
                        long int exp) 
{ 
    if (exp == 0) 
        return 1; 
  
    if (exp == 1) 
        return base % N; 
  
    long int t = exponentiation(base, exp / 2); 
    t = (t * t) % N; 
  
    // if exponent is even value 
    if (exp % 2 == 0) 
        return t; 
  
    // if exponent is odd value 
    else
        return ((base % N) * t) % N; 
} 
  
// Driver Code 
int main() 
{ 
    long int base = 5; 
    long int exp = 100000; 
  
    long int modulo = exponentiation(base, exp); 
    cout << modulo << endl; 
    return 0; 
} 
  
// This Code is contributed by mits 

Java

// Java program to compute exponential value under modulo 
// using binary exponentiation. 
import java.util.*; 
import java.lang.*; 
import java.io.*; 
  
class exp_sq { 
    static long N = 1000000007L; // prime modulo value 
    public static void main(String[] args) 
    { 
        long base = 5; 
        long exp = 100000; 
  
        long modulo = exponentiation(base, exp); 
        System.out.println(modulo); 
    } 
  
    static long exponentiation(long base, long exp) 
    { 
        if (exp == 0) 
            return 1; 
  
        if (exp == 1) 
            return base % N; 
  
        long t = exponentiation(base, exp / 2); 
        t = (t * t) % N; 
  
        // if exponent is even value 
        if (exp % 2 == 0) 
            return t; 
  
        // if exponent is odd value 
        else
            return ((base % N) * t) % N; 
    } 
} 

Python3

# Python3 program to compute  
# exponential value under 
# modulo using binary  
# exponentiation. 
  
# prime modulo value 
N = 1000000007; 
      
# Function code  
def exponentiation(bas, exp): 
    if (exp == 0): 
        return 1; 
    if (exp == 1): 
        return bas % N; 
      
    t = exponentiation(bas, int(exp / 2)); 
    t = (t * t) % N; 
      
    # if exponent is 
    # even value 
    if (exp % 2 == 0): 
        return t; 
          
    # if exponent is 
    # odd value 
    else: 
        return ((bas % N) * t) % N; 
  
# Driver code 
bas = 5; 
exp = 100000; 
  
modulo = exponentiation(bas, exp); 
print(modulo); 
  
# This code is contributed 
# by mits 

C#

// C# program to compute exponential 
// value under modulo using binary  
// exponentiation. 
using System; 
  
class GFG { 
      
    // prime modulo value 
    static long N = 1000000007L; 
      
    // Driver code 
    public static void Main() 
    { 
        long bas = 5; 
        long exp = 100000; 
  
        long modulo = exponentiation(bas, exp); 
        Console.Write(modulo); 
    } 
  
    static long exponentiation(long bas, long exp) 
    { 
        if (exp == 0) 
            return 1; 
  
        if (exp == 1) 
            return bas % N; 
  
        long t = exponentiation(bas, exp / 2); 
        t = (t * t) % N; 
  
        // if exponent is even value 
        if (exp % 2 == 0) 
            return t; 
  
        // if exponent is odd value 
        else
            return ((bas % N) * t) % N; 
    } 
} 
  
// This code is contributed by nitin mittal. 

PHP

<?php 
// PHP program to compute exponential 
// value under modulo using binary  
// exponentiation. 
  
// prime modulo value 
$N = 1000000007; 
      
// Function code  
function exponentiation($bas, $exp) 
{ 
    global $N ; 
    if ($exp == 0) 
        return 1; 
  
    if ($exp == 1) 
        return $bas % $N; 
  
    $t = exponentiation($bas,  
                        $exp / 2); 
    $t = ($t * $t) % $N; 
  
    // if exponent is 
    // even value 
    if ($exp % 2 == 0) 
        return $t; 
  
    // if exponent is 
    // odd value 
    else
        return (($bas % $N) * 
                 $t) % $N; 
} 
  
// Driver code 
$bas = 5; 
$exp = 100000; 
  
$modulo = exponentiation($bas, $exp); 
echo ($modulo); 
  
// This code is contributed by ajit 
?> 

Output :

754573817

$2^k$ -ary method:

In this algorithm we will be expanding the exponent in base 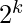$2^k$ (k>=1), which is somehow similar to above method except we are not using recursion this method uses comparatively less memory and time.

C++

// C++ program to compute exponential value using (2^k) 
// -ary method. 
#include<bits/stdc++.h> 
using namespace std; 
  
#define N 1000000007L; // prime modulo value 
  
long exponentiation(long base, long exp) 
{ 
    long t = 1L; 
    while (exp > 0)  
    { 
  
        // for cases where exponent 
        // is not an even value 
        if (exp % 2 != 0) 
            t = (t * base) % N; 
  
        base = (base * base) % N; 
        exp /= 2; 
    } 
    return t % N; 
} 
  
// Driver code 
int main() 
{ 
    long base = 5; 
    long exp = 100000; 
  
    long modulo = exponentiation(base, exp); 
    cout << (modulo); 
    return 0; 
} 
  
// This code is contributed by Rajput-Ji 

Java

// Java program to compute exponential value using (2^k) 
// -ary method. 
import java.util.*; 
import java.lang.*; 
import java.io.*; 
  
class exp_sq { 
    static long N = 1000000007L; // prime modulo value 
    public static void main(String[] args) 
    { 
        long base = 5; 
        long exp = 100000; 
  
        long modulo = exponentiation(base, exp); 
        System.out.println(modulo); 
    } 
  
    static long exponentiation(long base, long exp) 
    { 
        long t = 1L; 
        while (exp > 0) { 
  
            // for cases where exponent 
            // is not an even value 
            if (exp % 2 != 0) 
                t = (t * base) % N; 
  
            base = (base * base) % N; 
            exp /= 2; 
        } 
        return t % N; 
    } 
} 

Python3

# Python3 program to compute  
# exponential value  
# using (2^k) -ary method. 
  
# prime modulo value 
N = 1000000007;  
  
def exponentiation(bas, exp): 
    t = 1; 
    while(exp > 0):  
  
        # for cases where exponent 
        # is not an even value 
        if (exp % 2 != 0): 
            t = (t * bas) % N; 
  
        bas = (bas * bas) % N; 
        exp = int(exp / 2); 
    return t % N; 
  
# Driver Code  
bas = 5; 
exp = 100000; 
  
modulo = exponentiation(bas,exp); 
print(modulo); 
  
# This code is contributed 
# by mits 

C#

// C# program to compute  
// exponential value  
// using (2^k) -ary method. 
using System; 
  
class GFG 
{ 
// prime modulo value 
static long N = 1000000007L;  
  
static long exponentiation(long bas,  
                           long exp) 
{ 
    long t = 1L; 
    while (exp > 0)  
    { 
  
        // for cases where exponent 
        // is not an even value 
        if (exp % 2 != 0) 
            t = (t * bas) % N; 
  
        bas = (bas * bas) % N; 
        exp /= 2; 
    } 
    return t % N; 
} 
  
// Driver Code     
public static void Main () 
{ 
    long bas = 5; 
    long exp = 100000; 
  
    long modulo = exponentiation(bas,  
                                 exp); 
    Console.WriteLine(modulo); 
} 
} 
  
//This code is contributed by ajit 

PHP

<?php 
// PHP program to compute  
// exponential value  
// using (2^k) -ary method. 
  
// prime modulo value 
$N = 1000000007;  
  
function exponentiation($bas,  
                        $exp) 
{ 
    global $N;  
    $t = 1; 
    while ($exp > 0)  
    { 
  
        // for cases where exponent 
        // is not an even value 
        if ($exp % 2 != 0) 
            $t = ($t * $bas) % $N; 
  
        $bas = ($bas * $bas) % $N; 
        $exp = (int)$exp / 2; 
    } 
    return $t % $N; 
} 
  
// Driver Code  
$bas = 5; 
$exp = 100000; 
  
$modulo = exponentiation($bas,  
                         $exp); 
echo ($modulo); 
  
// This code is contributed 
// by ajit 
?> 

Output :

754573817

Applications:
Besides fast calculation of 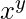$x^y$ this method have several other advantages, like it is used in cryptography, in calculating Matrix Exponentiation et cetera.

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.

My Personal Notes

Related Articles

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

C++

Java

Python3

C#

PHP

C++

Java

Python3

C#

PHP