Introduction To Grammar in Theory of Computation
Last Updated :
13 Apr, 2023
Prerequisite – Theory of Computation
Grammar :
It is a finite set of formal rules for generating syntactically correct sentences or meaningful correct sentences.
Constitute Of Grammar :
Grammar is basically composed of two basic elements –
- Terminal Symbols –
Terminal symbols are those which are the components of the sentences generated using a grammar and are represented using small case letter like a, b, c etc. - Non-Terminal Symbols –
Non-Terminal Symbols are those symbols which take part in the generation of the sentence but are not the component of the sentence. Non-Terminal Symbols are also called Auxiliary Symbols and Variables. These symbols are represented using a capital letter like A, B, C, etc.
Formal Definition of Grammar :
Any Grammar can be represented by 4 tuples – <N, T, P, S>
- N – Finite Non-Empty Set of Non-Terminal Symbols.
- T – Finite Set of Terminal Symbols.
- P – Finite Non-Empty Set of Production Rules.
- S – Start Symbol (Symbol from where we start producing our sentences or strings).
Production Rules :
A production or production rule in computer science is a rewrite rule specifying a symbol substitution that can be recursively performed to generate new symbol sequences. It is of the form α-> β where α is a Non-Terminal Symbol which can be replaced by β which is a string of Terminal Symbols or Non-Terminal Symbols.
Example-1 :
Consider Grammar G1 = <N, T, P, S>
T = {a,b} #Set of terminal symbols
P = {A->Aa,A->Ab,A->a,A->b,A->  } #Set of all production rules
S = {A} #Start Symbol
} #Set of all production rules
S = {A} #Start Symbol
As the start symbol is S then we can produce Aa, Ab, a,b, which can further produce strings where A can be replaced by the Strings mentioned in the production rules and hence this grammar can be used to produce strings of the form (a+b)*.
which can further produce strings where A can be replaced by the Strings mentioned in the production rules and hence this grammar can be used to produce strings of the form (a+b)*.
Derivation Of Strings :
A->a #using production rule 3
OR
A->Aa #using production rule 1
Aa->ba #using production rule 4
OR
A->Aa #using production rule 1
Aa->AAa #using production rule 1
AAa->bAa #using production rule 4
bAa->ba #using production rule 5
Example-2 :
Consider Grammar G2 = <N, T, P, S>
N = {A} #Set of non-terminals Symbols
T = {a} #Set of terminal symbols
P = {A->Aa, A->AAa, A->a, A-> } #Set of all production rules
S = {A} #Start Symbol
} #Set of all production rules
S = {A} #Start Symbol
As the start symbol is S then we can produce Aa, AAa, a,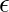 which can further produce strings where A can be replaced by the Strings mentioned in the production rules and hence this grammar can be used to produce strings of form (a)*.
which can further produce strings where A can be replaced by the Strings mentioned in the production rules and hence this grammar can be used to produce strings of form (a)*.
Derivation Of Strings :
A->a #using production rule 3
OR
A->Aa #using production rule 1
Aa->aa #using production rule 3
OR
A->Aa #using production rule 1
Aa->AAa #using production rule 1
AAa->Aa #using production rule 4
Aa->aa #using production rule 3
Equivalent Grammars :
Grammars are said to be equivalent if they produce the same language.
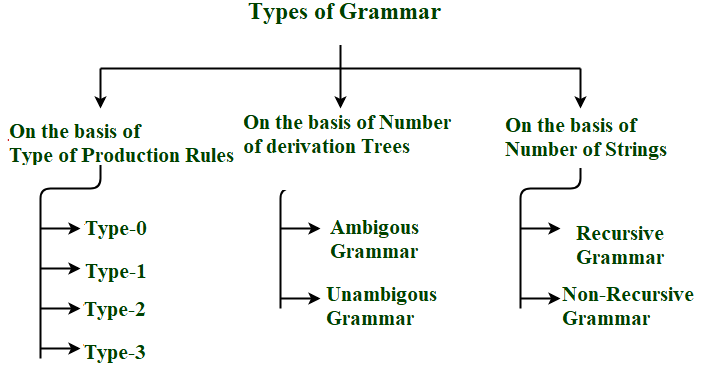
Different Types Of Grammars :
Grammar can be divided on basis of –
- Type of Production Rules
- Number of Derivation Trees
- Number of Strings
Share your thoughts in the comments
Please Login to comment...