Dijkstra’s shortest path algorithm using set in STL

Given a graph and a source vertex in graph, find shortest paths from source to all vertices in the given graph.

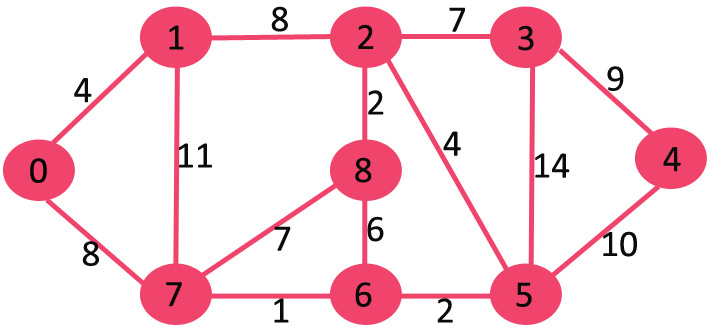
Input : Source = 0
Output : 
     Vertex   Distance from Source
        0                0
        1                4
        2                12
        3                19
        4                21
        5                11
        6                9
        7                8
        8                14

We have discussed Dijkstra’s shortest Path implementations. 

• Dijkstra’s Algorithm for Adjacency Matrix Representation (In C/C++ with time complexity O(v²)
• Dijkstra’s Algorithm for Adjacency List Representation (In C with Time Complexity O(ELogV))

The second implementation is time complexity wise better, but is really complex as we have implemented our own priority queue. STL provides priority_queue, but the provided priority queue doesn’t support decrease key and delete operations. And in Dijkstra’s algorithm, we need a priority queue and below operations on priority queue :

• ExtractMin : from all those vertices whose shortest distance is not yet found, we need to get vertex with minimum distance.
• DecreaseKey : After extracting vertex we need to update distance of its adjacent vertices, and if new distance is smaller, then update that in data structure.

Above operations can be easily implemented by set data structure of c++ STL, set keeps all its keys in sorted order so minimum distant vertex will always be at beginning, we can extract it from there, which is the ExtractMin operation and update other adjacent vertex accordingly if any vertex’s distance becomes smaller then delete its previous entry and insert new updated entry which is DecreaseKey operation.

Below is algorithm based on set data structure.  

1) Initialize distances of all vertices as infinite.
2) Create an empty set.  Every item of set is a pair
  (weight, vertex). Weight (or distance) is used
  as first item  of pair as first item is by default 
  used to compare two pairs.
3) Insert source vertex into the set and make its
   distance as 0.
4) While Set doesn't become empty, do following
    a) Extract minimum distance vertex from Set. 
       Let the extracted vertex be u.
    b) Loop through all adjacent of u and do 
       following for every vertex v.
           // If there is a shorter path to v
           // through u. 
           If dist[v] > dist[u] + weight(u, v)
               (i) Update distance of v, i.e., do
                     dist[v] = dist[u] + weight(u, v)
               (i) If v is in set, update its distance
                   in set by removing it first, then
                   inserting with new distance
               (ii) If v is not in set, then insert
                    it in set with new distance
               
5) Print distance array dist[] to print all shortest
   paths. 

Below is C++ implementation of above idea.

C++

// Program to find Dijkstra's shortest path using STL set
#include<bits/stdc++.h>
using namespace std;
# define INF 0x3f3f3f3f

// This class represents a directed graph using
// adjacency list representation
class Graph
{
    int V;    // No. of vertices

    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    list< pair<int, int> > *adj;

public:
    Graph(int V);  // Constructor

    // function to add an edge to graph
    void addEdge(int u, int v, int w);

    // prints shortest path from s
    void shortestPath(int s);
};

// Allocates memory for adjacency list
Graph::Graph(int V)
{
    this->V = V;
    adj = new list< pair<int, int> >[V];
}

void Graph::addEdge(int u, int v, int w)
{
    adj[u].push_back(make_pair(v, w));
    adj[v].push_back(make_pair(u, w));
}

// Prints shortest paths from src to all other vertices
void Graph::shortestPath(int src)
{
    // Create a set to store vertices that are being
    // processed
    set< pair<int, int> > setds;

    // Create a vector for distances and initialize all
    // distances as infinite (INF)
    vector<int> dist(V, INF);

    // Insert source itself in Set and initialize its
    // distance as 0.
    setds.insert(make_pair(0, src));
    dist[src] = 0;

    /* Looping till all shortest distance are finalized
       then setds will become empty    */
    while (!setds.empty())
    {
        // The first vertex in Set is the minimum distance
        // vertex, extract it from set.
        pair<int, int> tmp = *(setds.begin());
        setds.erase(setds.begin());

        // vertex label is stored in second of pair (it
        // has to be done this way to keep the vertices
        // sorted distance (distance must be first item
        // in pair)
        int u = tmp.second;

        // 'i' is used to get all adjacent vertices of a vertex
        list< pair<int, int> >::iterator i;
        for (i = adj[u].begin(); i != adj[u].end(); ++i)
        {
            // Get vertex label and weight of current adjacent
            // of u.
            int v = (*i).first;
            int weight = (*i).second;

            //    If there is shorter path to v through u.
            if (dist[v] > dist[u] + weight)
            {
                /*  If distance of v is not INF then it must be in
                    our set, so removing it and inserting again
                    with updated less distance.
                    Note : We extract only those vertices from Set
                    for which distance is finalized. So for them,
                    we would never reach here.  */
                if (dist[v] != INF)
                    setds.erase(setds.find(make_pair(dist[v], v)));

                // Updating distance of v
                dist[v] = dist[u] + weight;
                setds.insert(make_pair(dist[v], v));
            }
        }
    }

    // Print shortest distances stored in dist[]
    printf("Vertex   Distance from Source\n");
    for (int i = 0; i < V; ++i)
        printf("%d \t\t %d\n", i, dist[i]);
}

// Driver program to test methods of graph class
int main()
{
    // create the graph given in above figure
    int V = 9;
    Graph g(V);

    //    making above shown graph
    g.addEdge(0, 1, 4);
    g.addEdge(0, 7, 8);
    g.addEdge(1, 2, 8);
    g.addEdge(1, 7, 11);
    g.addEdge(2, 3, 7);
    g.addEdge(2, 8, 2);
    g.addEdge(2, 5, 4);
    g.addEdge(3, 4, 9);
    g.addEdge(3, 5, 14);
    g.addEdge(4, 5, 10);
    g.addEdge(5, 6, 2);
    g.addEdge(6, 7, 1);
    g.addEdge(6, 8, 6);
    g.addEdge(7, 8, 7);

    g.shortestPath(0);

    return 0;
}

Python3

import heapq

class Graph:
    def __init__(self, V):
        self.V = V
        self.adj = [[] for _ in range(V)]

    def addEdge(self, u, v, w):
        self.adj[u].append((v, w))
        self.adj[v].append((u, w))

    def shortestPath(self, src):
        # Create a priority queue to store vertices that are being processed
        pq = [(0, src)]

        # Create a list for distances and initialize all distances as infinite (INF)
        dist = [float('inf')] * self.V
        dist[src] = 0

        # Looping until all shortest distances are finalized
        while pq:
            # The first vertex in the priority queue is the minimum distance vertex
            d, u = heapq.heappop(pq)

            # Process the vertex if it has not been processed yet
            if d > dist[u]:
                continue

            # Iterate through all adjacent vertices of 'u'
            for v, weight in self.adj[u]:
                # If there is a shorter path to 'v' through 'u'
                if dist[v] > dist[u] + weight:
                    # Update the distance of 'v'
                    dist[v] = dist[u] + weight
                    heapq.heappush(pq, (dist[v], v))

        # Print shortest distances stored in dist[]
        print("Vertex   Distance from Source")
        for i in range(self.V):
            print(f"{i} \t\t {dist[i]}")

# Driver program to test methods of the Graph class
if __name__ == "__main__":
    # create the graph given in the above figure
    V = 9
    g = Graph(V)

    #    making the above shown graph
    g.addEdge(0, 1, 4)
    g.addEdge(0, 7, 8)
    g.addEdge(1, 2, 8)
    g.addEdge(1, 7, 11)
    g.addEdge(2, 3, 7)
    g.addEdge(2, 8, 2)
    g.addEdge(2, 5, 4)
    g.addEdge(3, 4, 9)
    g.addEdge(3, 5, 14)
    g.addEdge(4, 5, 10)
    g.addEdge(5, 6, 2)
    g.addEdge(6, 7, 1)
    g.addEdge(6, 8, 6)
    g.addEdge(7, 8, 7)

    g.shortestPath(0)

Javascript

// Program to find Dijkstra's shortest path using JavaScript Set
const INF = 0x3f3f3f3f;

// This class represents a directed graph using
// adjacency list representation
class Graph {
  constructor(V) {
    this.V = V; // No. of vertices
    // In a weighted graph, we need to store vertex
    // and weight pair for every edge
    this.adj = new Array(V);
    for (let i = 0; i < V; i++) {
      this.adj[i] = [];
    }
  }

  // function to add an edge to graph
  addEdge(u, v, w) {
    this.adj[u].push({ v, w });
    this.adj[v].push({ u, w });
  }

  // prints shortest path from s
  shortestPath(src) {
    // Create a set to store vertices that are being
    // processed
    const setds = new Set();

    // Create an array for distances and initialize all
    // distances as infinite (INF)
    const dist = new Array(this.V).fill(INF);

    // Insert source itself in Set and initialize its
    // distance as 0.
    setds.add([0, src]);
    dist[src] = 0;

    /* Looping till all shortest distance are finalized
       then setds will become empty    */
    while (setds.size !== 0) {
      // The first vertex in Set is the minimum distance
      // vertex, extract it from set.
      const tmp = setds.values().next().value;
      setds.delete(tmp);

      // vertex label is stored in second of pair (it
      // has to be done this way to keep the vertices
      // sorted distance (distance must be first item
      // in pair)
      const u = tmp[1];

      // 'i' is used to get all adjacent vertices of a vertex
      for (const i of this.adj[u]) {
        // Get vertex label and weight of current adjacent
        // of u.
        const { v, w } = i;

        //    If there is shorter path to v through u.
        if (dist[v] > dist[u] + w) {
          /*  If distance of v is not INF then it must be in
              our set, so removing it and inserting again
              with updated less distance.
              Note : We extract only those vertices from Set
              for which distance is finalized. So for them,
              we would never reach here.  */
          if (dist[v] !== INF) {
            setds.delete([dist[v], v]);
          }

          // Updating distance of v
          dist[v] = dist[u] + w;
          setds.add([dist[v], v]);
        }
      }
    }

    // Print shortest distances stored in dist[]
    console.log("Vertex   Distance from Source");
    for (let i = 0; i < this.V; i++) {
      console.log(`${i} \t\t ${dist[i]}`);
    }
  }
}

// Driver program to test methods of graph class
function main() {
// create the graph given in above figure
const V = 9;
const g = new Graph(V);
// making above shown graph
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);

g.shortestPath(0);
}

main();

Output

Vertex   Distance from Source
0          0
1          4
2          12
3          19
4          21
5          11
6          9
7          8
8          14

Time Complexity: Set in C++ are typically implemented using Self-balancing binary search trees. Therefore, time complexity of set operations like insert, delete is logarithmic and time complexity of above solution is O(ELogV)). 

Space Complexuty:O(V2) , here V is number of Vertices.

Dijkstra’s Shortest Path Algorithm using priority_queue of STL
This article is contributed by Utkarsh Trivedi.