Implementing Artificial Neural Network training process in Python
Last Updated :
08 Mar, 2024
An Artificial Neural Network (ANN) is an information processing paradigm that is inspired the brain. ANNs, like people, learn by example. An ANN is configured for a specific application, such as pattern recognition or data classification, through a learning process. Learning largely involves adjustments to the synaptic connections that exist between the neurons.
The brain consists of hundreds of billions of cells called neurons. These neurons are connected together by synapses which are nothing but the connections across which a neuron can send an impulse to another neuron. When a neuron sends an excitatory signal to another neuron, then this signal will be added to all of the other inputs of that neuron. If it exceeds a given threshold then it will cause the target neuron to fire an action signal forward — this is how the thinking process works internally.
In Computer Science, we model this process by creating “networks” on a computer using matrices. These networks can be understood as an abstraction of neurons without all the biological complexities taken into account. To keep things simple, we will just model a simple NN, with two layers capable of solving a linear classification problem.
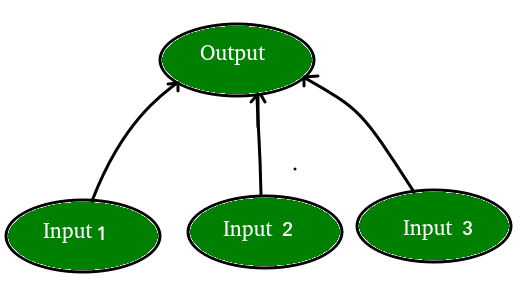
Let’s say we have a problem where we want to predict output given a set of inputs and outputs as training example like so:
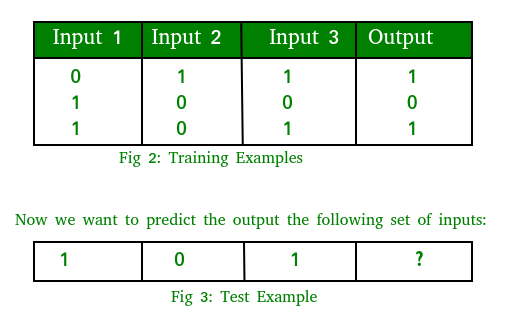
Note that the output is directly related to the third column i.e. the values of input 3 is what the output is in every training example in fig. 2. So for the test example output value should be 1.
The training process consists of the following steps:
- Forward Propagation:
Take the inputs, multiply by the weights (just use random numbers as weights)
Let Y = WiIi = W1I1+W2I2+W3I3
Pass the result through a sigmoid formula to calculate the neuron’s output. The Sigmoid function is used to normalize the result between 0 and 1:
1/1 + e-y
- Back Propagation
Calculate the error i.e the difference between the actual output and the expected output. Depending on the error, adjust the weights by multiplying the error with the input and again with the gradient of the Sigmoid curve:
Weight += Error Input Output (1-Output) ,here Output (1-Output) is derivative of sigmoid curve.
Note: Repeat the whole process for a few thousand iterations.
Let’s code up the whole process in Python. We’ll be using the Numpy library to help us with all the calculations on matrices easily. You’d need to install a numpy library on your system to run the code
Command to install numpy:
sudo apt -get install python-numpy
Implementation:
Python3
from joblib.numpy_pickle_utils import xrange
from numpy import *
class NeuralNet(object):
def __init__(self):
random.seed(1)
self.synaptic_weights = 2 * random.random((3, 1)) - 1
def __sigmoid(self, x):
return 1 / (1 + exp(-x))
def __sigmoid_derivative(self, x):
return x * (1 - x)
def train(self, inputs, outputs, training_iterations):
for iteration in xrange(training_iterations):
output = self.learn(inputs)
error = outputs - output
factor = dot(inputs.T, error * self.__sigmoid_derivative(output))
self.synaptic_weights += factor
def learn(self, inputs):
return self.__sigmoid(dot(inputs, self.synaptic_weights))
if __name__ == "__main__":
neural_network = NeuralNet()
inputs = array([[0, 1, 1], [1, 0, 0], [1, 0, 1]])
outputs = array([[1, 0, 1]]).T
neural_network.train(inputs, outputs, 10000)
print(neural_network.learn(array([1, 0, 1])))
|
Expected Output: After 10 iterations our neural network predicts the value to be 0.65980921. It looks not good as the answer should really be 1. If we increase the number of iterations to 100, we get 0.87680541. Our network is getting smarter! Subsequently, for 10000 iterations we get 0.9897704 which is pretty close and indeed a satisfactory output.
Share your thoughts in the comments
Please Login to comment...