Spatial filtering is the method of filtering out noise from images using a specific choice of spatial filters. Spatial filtering is defined as the technique of modifying a digital image by performing an operation on small regions or subsets of the original image pixels directly. Frequently, we use a mask to encompass the region of the image where this predefined operation is performed. A mask is basically a matrix used for computing the new image pixel intensities from the original one. A mask is used over a small region of the image and the center pixel value is replaced by the sum of the product of the original pixel values of the region and the filtering mask coefficients respectively at those points.
So if we define a 3 x 3 mask as follows:
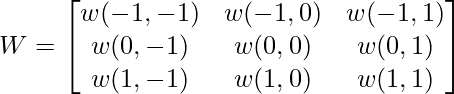
The mask is specified by its elements and that changes the characteristics of the mask, resulting in different effects with it. Usually a mask is of odd order because we have to replace the center pixel intensity value with a new value obtained by the mask operation.
Filtering creates a new pixel with coordinates equal to the coordinates of the center of the neighborhood of the image, which the,filter mask covers, and this center pixel value is equal to the value obtained by the filtering operation. A filtered output image is generated as the center of the mask visits each pixel of the image.
As shown below in the image, the value at the center pixel, after filtering, is obtained as :
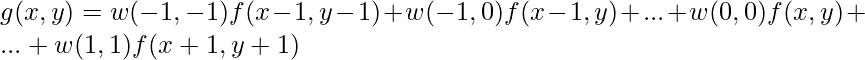
Here we are illustrating the operation of a 3 x 3 mask filter.
To get each new pixel value, the mask is shifted by one-pixel distance, the above operation is performed again and the new center pixel is assigned the computed value. This goes on for all the pixels of the image and finally, a new filtered image is formed with pixel intensities given by g(x,y).
If the operation performed on the image is linear, it is called linear spatial filtering. Otherwise, it is called non-linear spatial filtering.
Observe that the center coefficient of the filter mask w(0,0) aligns with the center pixel at location (x,y). For a mask of size m x n, we assume both m and n are odd positive integers, so m = 2a +1 and n = 2b +1, where a and b are again positive integers. In general, we can write linear spatial filtering of an image of size M x N with a filter of size m x n is given by the following expression :
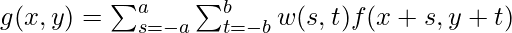
where x and y are varied so that each pixel in w visits every pixel f.
It is interesting to note that the above equation of linear spatial filtering bears resemblance to operations of 2D correlation and convolution operations. In fact, the following two equations define the operations of correlation and convolution respectively.
![Rendered by QuickLaTeX.com Cor[w(x,y),f(x,y)]=\sum_{s=-a}^{a}\sum_{t=-b}^{b}w(s,t)f(x+s,y+t) (1) Conv[w(x,y),f(x,y)]= w(x,y)*f(x,y)=\sum_{s=-a}^{a}\sum_{t=-b}^{b}w(s,t)f(x-s,y-t) (2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69e5c63936f45f851795828bba579070_l3.png)
It is clearly visible that the operation of convolution is exactly the same except that the filter is rotated by 180 degrees. It is also immediately understood that flipping f instead of the mask w gives the same result and hence we can safely that convolution is a commutative operation. The above equation has used a flipped f to compute the convolution. It is also evident that the correlation between two such functions is commutative.
If we implement Eq (1) as an algorithm, then to perform correlation we input w into the algorithm; whereas for convolution we input w but rotated by 180 degrees. Similarly, if we implement Eq (2) as an algorithm, then we input simply w for convolution; but for correlation, we have to input w flipped by 180 degrees.
Using correlation or convolution to perform spatial filtering is simply a matter of preference. In fact, both equations (1) as well as (2) can be made to perform filtering by a simple flipping of the mask. However, it is important to specify the filter mask coefficients in order to adequately perform the filtering operation it is designed to perform.
When we are interested to know the characteristic response of a filter mask, it is convenient to write the sum-of-products of filter coefficients and image intensities in the form:
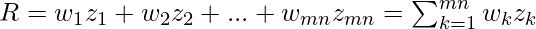
where wks are filtered mask coefficients and zks are corresponding image pixel intensities encompassed by the filter.
Spatial filters are used for image restoration and removal of noise. We discuss several useful filters commonly used in digital image processing for this purpose.
Smoothing or Averaging Filters:
Averaging the pixel intensity values of the image region encompassed by the mask results in a blurring or smoothing of the image. By replacing the value of every pixel in an image by the average of the intensity levels enco in the neighborhood encompassed by the filter mask, the process results in an image with reduced sharp transitions in intensities, hence an overall blurring or smoothing effect. This helps in reducing unwanted noise in the image.
Averaging filter masks can be defined as below.
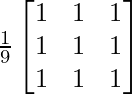
The above filter mask response can be expressed simply as
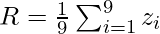
Let Sxy represent the set of coordinates in the image region encompassed by the mask. So the normal averaging filter, also known as the arithmetic mean filter, can alternatively be represented as :
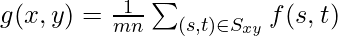
Another way is to have a weighted average.
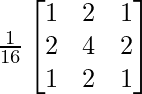
The most general weighted average filtering of an M x N image using a mask of size m x n is given by the following expression:
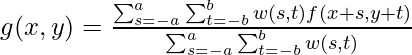
where x = 0,1,2,…,M-1 and y = 0,1,2,…,N-1; and m = 2a+1 and n = 2b+1.
Other Mean Filters:
The geometric mean filter is given by the following expression:
![Rendered by QuickLaTeX.com g(x,y)=[\prod_{(s,t)\in S_{xy}}^{}f(s,t)]^{1/mn}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c37a215e08da3b85e598829885b41fc_l3.png)
Each restored pixel is given by the product of the pixels in the sub-image region, raised to the power of 1/mn. The geometric mean filter obtains a greater smoothing effect as compared to the arithmetic mean filter.
The harmonic mean filter is :

The harmonic mean filter works well for the salt noise but fails for the pepper noise. It works well for Gaussian noise too.
Another unique type of filter is the contraharmonic mean filter.

Here Q is called the order of the filter. It is particularly well-suited for reducing or eliminating the effects of salt-and-pepper noise. For positive Q values, the filter eliminates pepper noise and for negative values, it eliminates salt noise. It cannot do both simultaneously. It is also interesting that for Q=1, the contra harmonic filter becomes the old arithmetic mean filter, while for Q=-1, it becomes a harmonic filter.
Order-Statistic Filters:
Order-statistic filters are spatial filters whose response is based on ordering or ranking the values of pixels contained in the image region encompassed by the filter. In essence, the response of such filters is totally dependent on the statistics of the pixel intensities contained in the mask region.
The median filter replaces the value of the pixel with the median of the intensity levels in the mask region.
![Rendered by QuickLaTeX.com g(x,y)=median_{(s,t)\in S_{xy}}[f(x,y)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-32d1f1c028873eac39b657738db8525a_l3.png)
Median filters provide excellent performance against noise, particularly for impulse noises, with considerably less blurring of images.
Max and min filters, as the name suggests, replace the pixel values with the maximum and minimum pixel intensities contained in the mask region respectively.
![Rendered by QuickLaTeX.com g(x,y)=max_{(s,t)\in S_{xy}}[f(x,y)] g(x,y)=min_{(s,t)\in S_{xy}}[f(x,y)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-60ebec45d1e079b4e7dba09714274d20_l3.png)
Max filter is used for finding the brightest points in the image. Also because pepper noise has very low-intensity values, it gets reduced by using the max filter. Similarly, the min filter is useful for finding the darkest points in the image and can work adequately to remove high-intensity salt noises.
The midpoint filter returns the midpoint between the maximum and minimum values in the region encompassed by the filter.
![Rendered by QuickLaTeX.com g(x,y)=\frac{1}{2}(min_{(s,t)\in S_{xy}}[f(x,y)]+max_{(s,t)\in S_{xy}}[f(x,y)])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-184dd16cdd77b2b03a4f0a1882e93a31_l3.png)
It works best for randomly distributed noise like Gaussian or uniform noise.
The alpha-trimmed filter is another type of order-statistic filter. If we delete the d/2 lowest and d/2 highest intensity values of f(s,t) in the region Sxy , then let fr(s,t) denote the remaining pixels. Now if we take an average over these remaining pixel intensities, then it forms what is commonly called an alpha-trimmed mean filter.
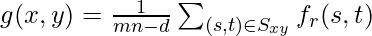
where d can range between 0 and mn-1. If d=0, the alpha-trimmed filter reduces to the plain arithmetic mean filter. It is particularly useful against combinations of salt-and-pepper noise and Gaussian noise.
Share your thoughts in the comments
Please Login to comment...