Hypercube Interconnection
Last Updated :
10 May, 2020
Hypercube (or Binary n-cube multiprocessor) structure represents a loosely coupled system made up of N=2n processors interconnected in an n-dimensional binary cube. Each processor makes a made of the cube. Each processor makes a node of the cube. Therefore, it is customary to refer to each node as containing a processor, in effect it has not only a CPU but also local memory and I/O interface. Each processor has direct communication paths to n other neighbor processors. These paths correspond to the cube edges.
There are 2 distinct n-bit binary addresses which can be assigned to the processors. Each processor address differs from that of each of its n neighbors by exactly one bit position.
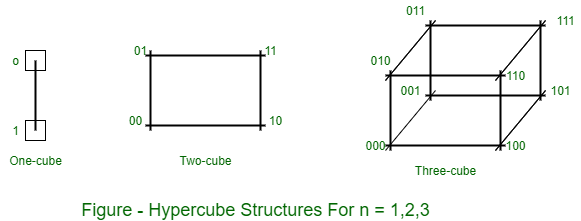
- Hypercube structure for n= 1, 2 and 3.
- A one cube structure contains n = 1 and 2n = 2.
- It has two processors interconnected by a single path.
- A two-cube structure contains n=2 and 2n=4.
- It has four nodes interconnected as a cube.
- An n-cube structure contains 2n nodes with a processor residing in each node.
Each node is assigned a binary address in such a manner, that the addresses of two neighbors differ in exactly one bit position. For example, the three neighbors of the node with address 100 are 000, 110, and 101 in a three-cube structure. Each of these binary numbers differs from address 100 by one bit value.
Routing messages through an n-cube structure may take from one to n links from a source node to a destination node.
Example:
In a three-cube structure, node 000 may communicate with 011 (from 000 to 010 to 011 or from 000 to 001 to 011). It should cross at least three links to communicate from node 000 to node 111. A routing procedure is designed by determining the exclusive-OR of the source node address with the destination node address. The resulting binary value will have 1 bits corresponding to the axes on which the two nodes differ. Then, message is transmitted along any one of the exes.
For example, a message at node 010 going to node 001 produces an exclusive-OR of the two addresses equal to 011 in a three-cube structure. The message can be transmitted along the second axis to node 000 and then through the third axis to node 001.
Share your thoughts in the comments
Please Login to comment...