How to calculate the distance between Two Points?

Question

GeeksforGeeks · Accepted Answer

The length of the line segment connecting two points is defined as the distance between them. The length of the line segment connecting the specified coordinates can be used to compute the distance between two points in coordinate geometry. Let’s look at the formula for calculating the distance between two points in a two-dimensional or three-dimensional plane.

What is the Distance Between Two Points?

The distance of the line segment connecting any two points is the distance between them. There is only one line that connects two points. As a result, the distance between two points may be computed by determining the length of the line segment that connects the two spots. For example, if A and B are two points and A B = 20 cm, it implies the distance between A and B is 20 cm.

The length of the line segment connecting two points is the distance between them (but this CANNOT be the length of the curve joining them). It is important to note that the distance between two places is always positive.

Distance Between Two Points Formula

The distance formula is used to determine the distance between two points using the provided coordinates. We use the 2D distance formula or the Euclidean distance formula to calculate the distance between any two points in the 2-D plane.

Formula for Distance Between Two Points

The formula for the distance, d, between two points whose coordinates are (x₁, y₁) and (x_2,y₂) is

$d = \sqrt{[(x_2 - x_1 )^2 +(y_2 - y_1)^2]}$

This is called the Distance Formula.

To find the distance between two points given in 3-D plane, we can apply the 3D distance formula, given as,

$d = \sqrt{[(x_2 - x_1 )^2 +(y_2 - y_1)^2 + (z_2 - z_1 )^2]}$

Derivation of Formula for Distance Between Two Points

To obtain the formula for calculating the distance between two points on a two-dimensional plane, assume there are two points with the coordinates, A (x₁,y₁) and B (x₂,y₂). Following that, we will suppose that the line segment connecting A and B is AB = d. We will now plot the specified points on the coordinate plane and connect them with a line.

Next, we will construct a right-angled triangle using AB as the hypotenuse.

Using Pythagoras Theorem,

AB²= AC²+ BC²

d² = (x₂−x₁)² + (y₂−y₁)²

Here, the vertical distance between the given points is | y₂ – y₁|

The horizontal distance between the given points is | x₂ – x₁ |

$d = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2] }$ (Taking square root on both sides)

Thus, the distance formula to find the distance between two points is proved.

Using similar steps and concept, we can also derive the formula to find the distance between two points given in the 3D plane.

Steps to find the distance between two points

The following steps may be used to determine the distance between two places using the provided coordinates:

Make a note of the coordinates of the two given points on the coordinate plane as follows: A(x₁,y₁) and B(x₂,y₂).
We may use the distance formula to calculate the distance between two places, $d = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}.$
Express the given answer in units.

Note: We can apply the 3D distance formula in case the two points are given in 3D plane,

Sample Problems

Problem 1: Find the distance between the two points with the coordinates given as, A(1,5) and B (2,7).

Solution:

Let (x₁, y₁) be (2,7) and (x₂, y₂) be (1,5).

The distance d between the points : $d = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}$

$\implies \sqrt{[(2-1)^2 + (7-5)^2]}$

$\implies \sqrt{[1^2 + 2^2]}$

$\implies \sqrt{(1+4)} = \sqrt{5} \ units$

The distance between the two points is √5 units.

Problem 2: Find the distance between the two points with the coordinates given as, P (2,-6,2) and Q(7, 3, 1).

Solution:

Let (x₁, y₁, z₁) be P (2,-6,2) and (x₂, y₂, z₂) be Q (7,3,1).

The distance d between the points P and Q : $d = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2+(z_2-z_1)^2]}$

$\implies \sqrt{(7-2)^2+(3-(-6))^2+(1-2)^2)}$

$\implies \sqrt{ 5^2+9^2+(-1)^2}$

$\implies \sqrt{25+81+1}$

$\implies \sqrt{107}\ units$

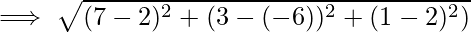
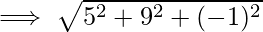
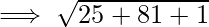
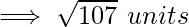
Problem 3: Prove that the vertices of a right-angled triangle are the points (3, 4), (7, 4), and (3, 8).

Solution:

Let us say the given points be:

P = (3, 4)

Q = (7, 4)

R = (3, 8)

Now, we will find each vertices of the right-angle triangle by distance formula.

$AB=\sqrt{(7-3)^2+(4-4)^2}=\sqrt{4^2}=4units$

$BC=\sqrt{(3-7)^2+(8-4)^2}=\sqrt{(-4)^2+4^2}=4\sqrt{2}units$

$AC=\sqrt{(3-3)^2+(8-4)^2}=\sqrt{4^2}=4units$

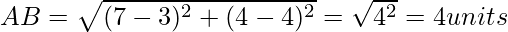
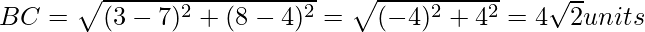
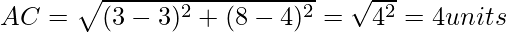
As we know the length of the sided of the right-angled triangle, by Pythagoras Theorem;

AB²+ AC²= BC²

4²+4²=(4√2)²

16+16 = 32⟹32 = 32

This proves that ABC is a right-angle triangle.

Distance Between Two Points in Complex Plane

The distance between two points in a complex plane or two complex numbers z₁=a+ib and z₂=c+id in the complex ⟹1−2k=9+4k plane is the distance between points (a, b) and (c, d), given as,

$| z_2 - z_1 |= \sqrt{[(a − c)^2 + (b − d)^2]}$

Problem 4: Find the distance between the two complex numbers z₁= 2−5i and z₂= 7+7i

Solution:

Here, we have two complex numbers z₁= 2-5i and z₂= 7+7i.

The distance between these complex numbers is equidistance to the two points in the plane, with coordinates, (2,-5) and (7,7).

Thus, distance between the two points is

$\implies \sqrt{(7-2)^2+(7-(-5))^2}$

$\implies \sqrt{5^2+12^2}\implies \sqrt{25+144}$

$\implies \sqrt{169}\implies13\ units$

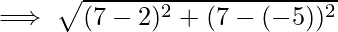
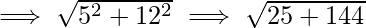
Hence, the distance between two complex numbers z_1=2-5i and z_2=7+7i is 13 units.

Problem 5: A complex number ω is 6 units apart from z₁= -3 – i and 6 units apart from z₂= 3 + 5i. Check whether the triangle formed by ω, z₁, z₂ is right – angled or not.

Solution:

There are 3 complex numbers ω, z₁, z₂.

As we know the distance between ω and z₁ is 6 units and distance between ω and z₂ is 6 units.

Given, ω, z₁= 6 units

ω, z₂= 6 units

Now, we will find the distance between z₁and z₂ by using distance formula.

$z_1z_2=\sqrt{(3-(-3)+(5-(-1))}$

$\implies \sqrt{6^2+6^2}$ $\implies \sqrt{36+36}\implies \sqrt{72}$

$\implies 6\sqrt{2} units.$

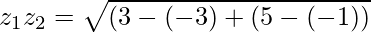
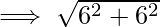
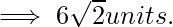
By Pythagoras Theorem, we have;

(z₁z₂)²=(ωz₁)²+(ωz₂)²

$\implies (6\sqrt{2})^2=6^2+6^2$

$\implies 72=36+36\implies 72=72$

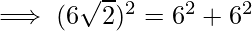
Hence, we conclude that the given triangle is right-angle triangle.

Problem 6: Find a point on the x-axis that is equidistant from the points (1, -2) and (-2, -3).

Solution:

We know that any point on the x-axis has an y-coordinate of 0. As a result, we consider the point equidistant from the provided points to be (k,0). i.e., Distance between ( k,0) and (1, -2) = Distance between (k, 0) and (-2, -3).

$\implies \sqrt{[(1-k)^2 + (-2-0)^2]} = \sqrt{[(-2-k)^2 + (-3-0)^2]}$

$\implies 12 + k^2 -2k + 4 = 4+ k^2 +4k + 9$

$\implies 1-2k= 9+ 4k$

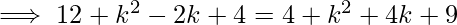
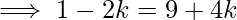
\implies -4k-2k= 9-1

$\implies -6k=8$

$\implies k=\frac{-4}{3}$

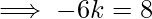
Therefore, the required point is (k, 0) = $(\frac{-4}{3}, 0).$

Suggest improvement

Share your thoughts in the comments

How to calculate the distance between Two Points?

What is the Distance Between Two Points?

Distance Between Two Points Formula

Sample Problems

Distance Between Two Points in Complex Plane

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?