Program to calculate distance between two points

You are given two coordinates (x1, y1) and (x2, y2) of a two-dimensional graph. Find the distance between them.

Examples: 

Input : x1, y1 = (3, 4)
        x2, y2 = (7, 7)
Output : 5

Input : x1, y1 = (3, 4) 
        x2, y2 = (4, 3)
Output : 1.41421

Calculate the distance between two points.

We will use the distance formula derived from Pythagorean theorem. The formula for distance between two point (x1, y1) and (x2, y2) is
Distance = 
We can get above formula by simply applying Pythagoras theorem

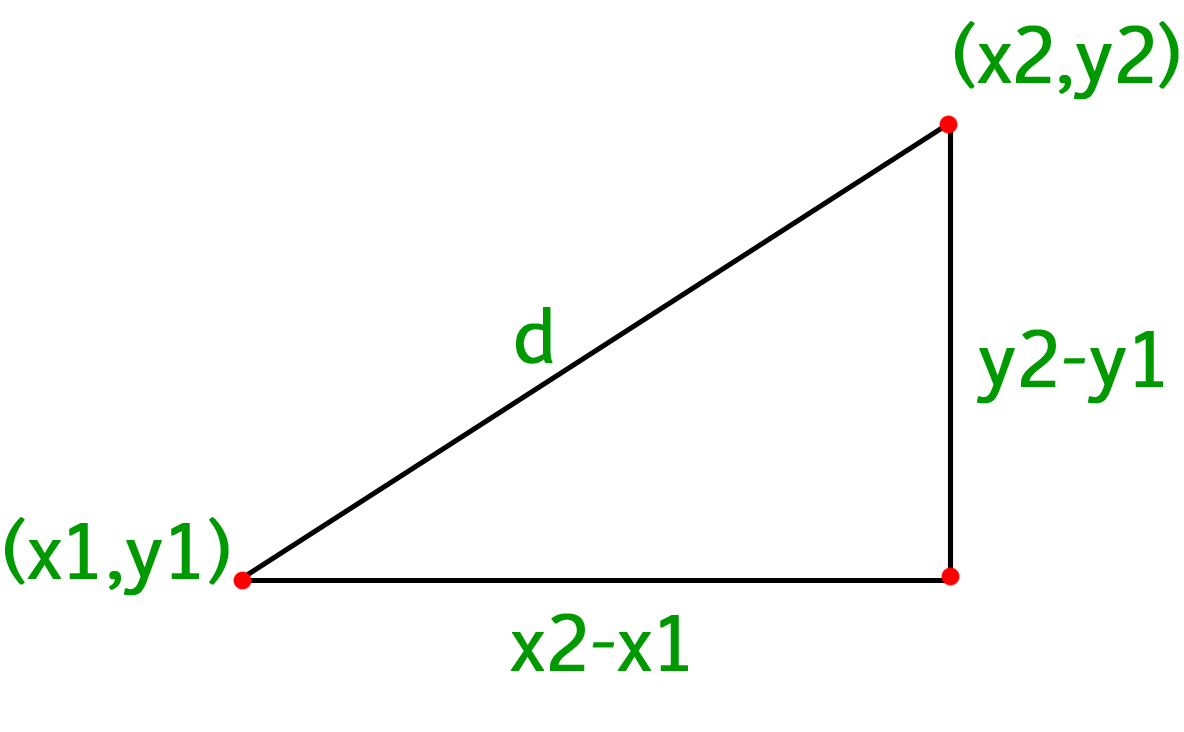
calculate distance between two points

Below is the implementation of above idea.

Method 1: Without using the inbuilt library,

Python3

def distance(x1, y1, x2, y2):

  # Calculating distance

  return (((x2 - x1)**2 +(y2 - y1)**2)**0.5)

# Drivers Code

print( distance(3, 4, 4, 3))

Output

1.4142135623730951

Time Complexity: O(1)
Auxiliary Space: O(1)

Method 2: Using the inbuilt library,

C++

#include <bits/stdc++.h>
using namespace std;

// Function to calculate distance
float distance(int x1, int y1, int x2, int y2)
{
    // Calculating distance
    return sqrt(pow(x2 - x1, 2) + pow(y2 - y1, 2) * 1.0);
}

// Drivers Code
int main()
{
    cout << distance(3, 4, 4, 3);
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

C

#include <math.h>
#include <stdio.h>

// Function to calculate distance
float distance(int x1, int y1, int x2, int y2)
{
    // Calculating distance
    return sqrt(pow(x2 - x1, 2) + pow(y2 - y1, 2) * 1.0);
}

// Drivers Code
int main()
{
    printf("%f", distance(3, 4, 4, 3));
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

Java

// Java code to compute distance

class GFG {
    // Function to calculate distance
    static double distance(int x1, int y1, int x2, int y2)
    {
        // Calculating distance
        return Math.sqrt(Math.pow(x2 - x1, 2)
                         + Math.pow(y2 - y1, 2) * 1.0);
    }
    // Driver code
    public static void main(String[] args)
    {
        System.out.println(
            Math.round(distance(3, 4, 4, 3) * 100000.0)
            / 100000.0);
    }
}

// This code is contributed by Aditya Kumar (adityakumar129)

Python3

# Python3 program to calculate
# distance between two points

import math

# Function to calculate distance
def distance(x1 , y1 , x2 , y2):

    # Calculating distance
    return math.sqrt(math.pow(x2 - x1, 2) +
                math.pow(y2 - y1, 2) * 1.0)

# Drivers Code
print("%.6f"%distance(3, 4, 4, 3))

# This code is contributed by "Sharad_Bhardwaj".

C#

// C# code to compute distance
using System;

class GFG
{
    // Function to calculate distance
    static double distance(int x1, int y1, int x2, int y2)
    {
        // Calculating distance
        return Math.Sqrt(Math.Pow(x2 - x1, 2) +
                      Math.Pow(y2 - y1, 2) * 1.0);
    }

    // Driver code
    public static void Main ()
    {
        Console.WriteLine(Math.Round(distance(3, 4, 4, 3)
                                   * 100000.0)/100000.0);
    }
}

// This code is contributed by
// vt_m.

PHP

<?php
// PHP code to compute distance

// Function to calculate distance
function distance($x1, $y1, $x2, $y2)
{

    // Calculating distance
    return sqrt(pow($x2 - $x1, 2) +
                pow($y2 - $y1, 2) * 1.0);
}

// Driver Code
echo(distance(3, 4, 4, 3));

// This code is contributed by Ajit.
?>

Javascript

<script>

// Function to calculate distance
function distance(x1, y1, x2,  y2)
{
    // Calculating distance
    return Math.sqrt(Math.pow(x2 - x1, 2) +
                Math.pow(y2 - y1, 2) * 1.0);
}

// Drivers Code
document.write(distance(3, 4, 4, 3));

// This code is contributed by noob2000.
</script>

Output

1.41421

Time Complexity: O(1)
Auxiliary Space: O(1)