How to find the distance between two points?
Last Updated :
28 Nov, 2021
The length of the wire used to cover the length between two points is the distance between two points. In case the two points are situated on the same horizontal or same vertical line, the distance between the two points can be calculated by subtracting the coordinates that are not the same.
The distance formula can be used to compute the distance that is measured between the two line segments. The distance formula can be used for the computation of the sum of the lengths of all the sides of a polygon, perimeter of polygons on a coordinate plane, the area of polygons, etc. The lengths of sides of triangles can also be computed using the distance formula. The type of triangle, scalene, isosceles or equilateral can also be determined using the distance formula.
Distance Between Two Points
The x coordinate of the point is known as the abscissa whereas the y coordinate is known as the ordinate. The distance formula can be used to calculate the distance between two points of the xy-plane. An ordered pair (x, y) represents the co-ordinate of the point, where x-coordinate is defined as the distance of the point from the x-axis and y-coordinate is the distance of the point from the y-axis.
The following formula can be used to find the distance between two points in a 2d plane:
Consider any two arbitrary points A(x1,y1) and B(x2,y2) on the given coordinate axis. The distance between the following two points is given as follows:
d =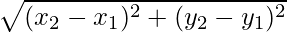

Derivation of Distance Formula
In the right-angled triangle ABC, we have,
By the Pythagoras theorem,
AB2 = AC2 + BC2
Since, we have derived the formula of distance calculation between two points, therefore,
The distance between points A and C is calculated as (x2 – x1)2
The distance between points A and C is calculated as (y2 – y1)2
The distance, d is calculated as,
d2 = (x2 – x1)2 + (y2 – y1)2
Now,
Taking the square root on both sides,
d = 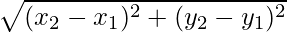
This is the called the distance between two points formula.
Sample Questions
Question 1. Find the distance between A(3, 4) and B(5, 8)
Solution:
Here to find the distance between point A and B
Applying distance formula
d = 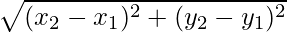
d = 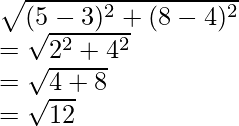
Distance between A and B is √12 or 3.46
Question 2. Calculate the distance between the points X(-10, -12) and Y(-2, 3)?
Solution:
Here to find the distance between point X and Y
Applying distance formula
d = 
d = 
d = 17
Distance between X and Y is 17.
Question 3. Find the distance between P(-10, -20) and Q(-1, -2)?
Solution:
Here to find the distance between P and Q
Applying distance formula
d = 
d = 
Distance between P and Q is √405 or 20.12.
Question 4. Find the distance between two points A(445, 550) and B(-445, -550)?
Solution:
Here to find the distance between A and B
Applying distance formula
d = 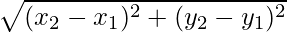
d = 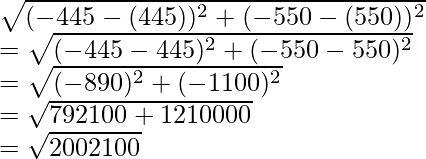
Distance between A and B is √2002100 or 1414.95.
Share your thoughts in the comments
Please Login to comment...