How does Floyd’s slow and fast pointers approach work?
Last Updated :
11 Jan, 2023
We have discussed Floyd’s fast and slow pointer algorithms in Detect loop in a linked list.
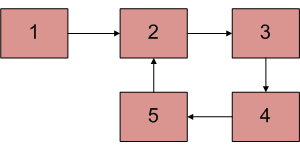
The algorithm is to start two pointers, slow and fast from head of linked list. We move slow one node at a time and fast two nodes at a time. If there is a loop, then they will definitely meet. This approach works because of the following facts. 1) When slow pointer enters the loop, the fast pointer must be inside the loop.
Let fast pointer be distance k from slow. 2) Now if consider movements of slow and fast pointers, we can notice that distance between them (from slow to fast) increase by one after every iteration. After one iteration (of slow = next of slow and fast = next of next of fast), distance between slow and fast becomes k+1, after two iterations, k+2, and so on. When distance becomes n, they meet because they are moving in a cycle of length n. For example, we can see in below diagram, initial distance is 2. After one iteration, distance becomes 3, after 2 iterations, it becomes 4. After 3 iterations, it becomes 5 which is distance 0. And they meet.
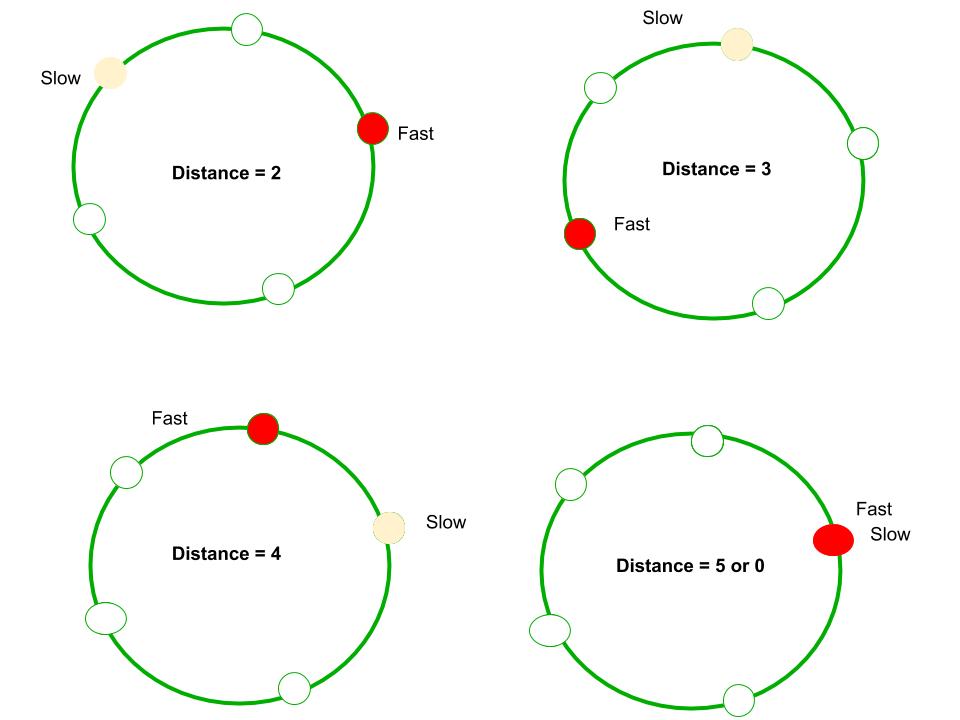
Alternate Proof:
- Let us give index to all the nodes of the loop starting from 0
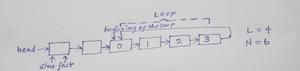
Index is assigned to each node of the loop
- Let the length of the Loop be L
- Let us observe the movement of the Slow pointer from the beginning of the loop along with iterations.
|
Iteration
i
|
Index of the node pointed by
Slow pointer
|
|
1
|
1
|
|
2
|
2
|
|
3
|
3
|
|
4
|
4
|
|
…
|
|
L-1
|
L-1
|
|
L
|
0
|
|
L+1
|
1
|
|
and so on…
|
From the table , we can say that
Index of the node pointed by Slow pointer after iteration i = i mod L
- Let us observe the movement of Fast pointer from the beginning of the loop along with iterations.
|
Iteration
i
|
Index of the node pointed by
Fast pointer
|
|
1
|
2
|
|
2
|
4
|
|
3
|
6
|
|
4
|
8
|
|
…
|
|
(L-1)/2 , if L is odd
(L-2)/2 , if L is even
|
L-1 , if L is odd
L-2 , if L is even
|
|
((L-1)/2)+1 , if L is odd
((L-2)/2)+1 , if L is even
|
1 , if L is odd
0 , if L is even
|
|
and so on…
|
From the table, we can say that
Index of the node pointed by Fast pointer after iteration i = ( 2 x i ) mod L
- One thing to note is that , by the time slow pointer reaches the beginning of the loop , the fast pointer will be d nodes away from the beginning of the loop
- 0 <= d <= L-1
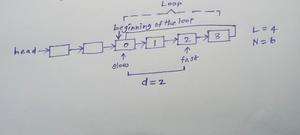
By the time slow pointer reaches the beginning of the loop, fast pointer is d nodes away from the beginning of the loop
- Hence for all the consequent iterations too , the Fast pointer will be d nodes away from the node that it would point if it started from beginning of the loop
- Hence we have
Index of the node pointed by Fast pointer after iteration i = ( ( 2 x i ) + d ) mod L
Now we have both the equations :
- Index of the node pointed by Slow pointer after iteration i = i mod L
- Index of the node pointed by Fast pointer after iteration i = ( ( 2 x i ) + d ) mod L
Now assign i = c , where c = L – d
L – Length of the loop
d – distance between the Fast pointer and beginning of the loop , when Slow pointer reaches the beginning of the loop
Since 0 <= d <= L-1 , implies 1 <= c <= L
- Index of the node pointed by Slow pointer after iteration i = i mod L
= c mod L
= 0 , ( if c = L )
c , ( if c < L )
- Index of the node pointed by Fast pointer after iteration i = ( ( 2 x i ) + d ) mod L
= ( ( 2 x c ) + d ) mod L
= ( 2c + d ) mod L
= ( c + c + d ) mod L
= ( c + L ) mod L , Since c = L – d , implies c + d = L
= c mod L
= 0 , ( if c = L )
c , ( if c < L )
- Now Both the Slow pointer and the Fast pointer are pointing to the same node
- Hence proved
How does cycle removal algorithm work? Please see method 3 of Detect and Remove Loop in a Linked List
Implementation:
Java
class LinkedList {
Node head;
class Node {
int data;
Node next;
Node(int d)
{
data = d;
next = null;
}
}
public void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
void detectLoop()
{
Node slow_p = head, fast_p = head;
int flag = 0;
while (slow_p != null && fast_p != null
&& fast_p.next != null) {
slow_p = slow_p.next;
fast_p = fast_p.next.next;
if (slow_p == fast_p) {
flag = 1;
break;
}
}
if (flag == 1)
System.out.println("Loop found");
else
System.out.println("Loop not found");
}
public static void main(String args[])
{
LinkedList llist = new LinkedList();
llist.push(20);
llist.push(4);
llist.push(15);
llist.push(10);
llist.head.next.next.next.next = llist.head;
llist.detectLoop();
}
}
|
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
};
void push(Node** head_ref, int new_data)
{
Node* new_node = new Node();
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
int detectLoop(Node* list)
{
Node *slow_p = list, *fast_p = list;
while (slow_p && fast_p && fast_p->next) {
slow_p = slow_p->next;
fast_p = fast_p->next->next;
if (slow_p == fast_p) {
return 1;
}
}
return 0;
}
int main()
{
Node* head = NULL;
push(&head, 20);
push(&head, 4);
push(&head, 15);
push(&head, 10);
head->next->next->next->next = head;
if (detectLoop(head))
cout << "Loop found";
else
cout << "No Loop";
return 0;
}
|
Javascript
<script>
let head;
class Node
{
constructor(d)
{
this.data = d;
this.next = null;
}
}
function push(new_data)
{
let new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
function detectLoop()
{
let slow_p = head, fast_p = head;
let flag = 0;
while (slow_p != null && fast_p != null &&
fast_p.next != null)
{
slow_p = slow_p.next;
fast_p = fast_p.next.next;
if (slow_p == fast_p)
{
flag = 1;
break;
}
}
if (flag == 1)
document.write("Loop found<br>");
else
document.write("Loop not found<br>");
}
push(20);
push(4);
push(15);
push(10);
head.next.next.next.next = head;
detectLoop();
</script>
|
Python
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
def push(self, new_data):
new_node = Node(new_data)
new_node.next = self.head
self.head = new_node
def printList(self):
temp = self.head
while(temp):
print temp.data,
temp = temp.next
def detectLoop(self):
slow_p = self.head
fast_p = self.head
while(slow_p and fast_p and fast_p.next):
slow_p = slow_p.next
fast_p = fast_p.next.next
if slow_p == fast_p:
return
llist = LinkedList()
llist.push(20)
llist.push(4)
llist.push(15)
llist.push(10)
llist.head.next.next.next.next = llist.head
if(llist.detectLoop()):
print "Found Loop"
else:
print "No Loop"
|
C#
using System;
public class LinkedList {
Node head;
public class Node {
public int data;
public Node next;
public Node(int d)
{
data = d;
next = null;
}
}
public void push(int new_data)
{
Node new_node = new Node(new_data);
new_node.next = head;
head = new_node;
}
Boolean detectLoop()
{
Node slow_p = head, fast_p = head;
while (slow_p != null && fast_p != null
&& fast_p.next != null) {
slow_p = slow_p.next;
fast_p = fast_p.next.next;
if (slow_p == fast_p) {
return true;
}
}
return false;
}
public static void Main(String[] args)
{
LinkedList llist = new LinkedList();
llist.push(20);
llist.push(4);
llist.push(15);
llist.push(10);
llist.head.next.next.next.next = llist.head;
Boolean found = llist.detectLoop();
if (found) {
Console.WriteLine("Loop Found");
}
else {
Console.WriteLine("No Loop");
}
}
}
|
Share your thoughts in the comments
Please Login to comment...