Heteroscedasticity in Regression Analysis
Last Updated :
07 Jun, 2019
Prerequisite:
Linear Regression
In Simple Linear Regression or Multiple Linear Regression we make some basic assumptions on the error term
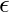
.
Simple Linear Regression:
(1) 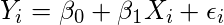
Multiple Linear Regression:
(2) 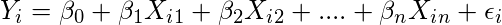
Assumptions:
1. Error has zero mean
2. Error has constant variance
3. Errors are uncorrelated
4. Errors are normally distributed
The
second assumption is known as
Homoscedasticity and therefore, the violation of this assumption is known as
Heteroscedasticity.
Homoscedasticity vs Heteroscedasticity:

Therefore, in simple terms, we can define
heteroscedasticity as the condition in which the variance of error term or the residual term in a regression model varies. As you can see in the above diagram, in case of homoscedasticity, the data points are equally scattered while in case of heteroscedasticity the data points are not equally scattered.
Possible reasons of arising Heteroscedasticity:
- Often occurs in those data sets which have a large range between the largest and the smallest observed values i.e. when there are outliers.
- When model is not correctly specified.
- If observations are mixed with different measures of scale.
- When incorrect transformation of data is used to perform the regression.
- Skewness in the distribution of a regressor, and may be some other sources.
Effects of Heteroscedasticity:
- As mentioned above that one of the assumption (assumption number 2) of linear regression is that there is no heteroscedasticity. Breaking this assumption means that OLS (Ordinary Least Square) estimators are not the Best Linear Unbiased Estimator(BLUE) and their variance is not the lowest of all other unbiased estimators.
- Estimators are no longer best/efficient.
- The tests of hypothesis (like t-test, F-test) are no longer valid due to the inconsistency in the co-variance matrix of the estimated regression coefficients.
Identifying Heteroscedasticity with residual plots:
As shown in the above figure, heteroscedasticity produces either outward opening funnel or outward closing funnel shape in residual plots.
Identifying Heteroscedasticity Through Statistical Tests:
The presence of heteroscedasticity can also be quantified using the algorithmic approach. There are some statistical tests or methods through which the presence or absence of heteroscedasticity can be established.
- The Breush – Pegan Test: It tests whether the variance of the errors from regression is dependent on the values of the independent variables. In that case, heteroskedasticity is present.
- White test: White test establishes whether the variance of the errors in a regression model is constant. To test for constant variance one undertakes an auxiliary regression analysis: this regresses the squared residuals from the original regression model onto a set of regressors that contain the original regressors along with their squares and cross-products.
Corrections for heteroscedasticity:
- We can use different specification for the model.
- Weighted Least Squares method is one of the common statistical method. This is the generalization of ordinary least square and linear regression in which the errors co-variance matrix is allowed to be different from an identity matrix.
- Use MINQUE: The theory of Minimum Norm Quadratic Unbiased Estimation (MINQUE) involves three stages. First, defining a general class of potential estimators as quadratic functions of the observed data, where the estimators relate to a vector of model parameters. Secondly, specifying certain constraints on the desired properties of the estimators, such as unbiasedness and third, choosing the optimal estimator by minimizing a “norm” which measures the size of the covariance matrix of the estimators.
Reference:
https://en.wikipedia.org/wiki/Heteroscedasticity
Share your thoughts in the comments
Please Login to comment...