Height of binary tree considering even level leaves only

Find the height of the binary tree given that only the nodes on the even levels are considered valid leaf nodes. 
The height of a binary tree is the number of edges between the tree’s root and its furthest leaf. But what if we bring a twist and change the definition of a leaf node? Let us define a valid leaf node as the node that has no children and is at an even level (considering the root node as an odd level node). 

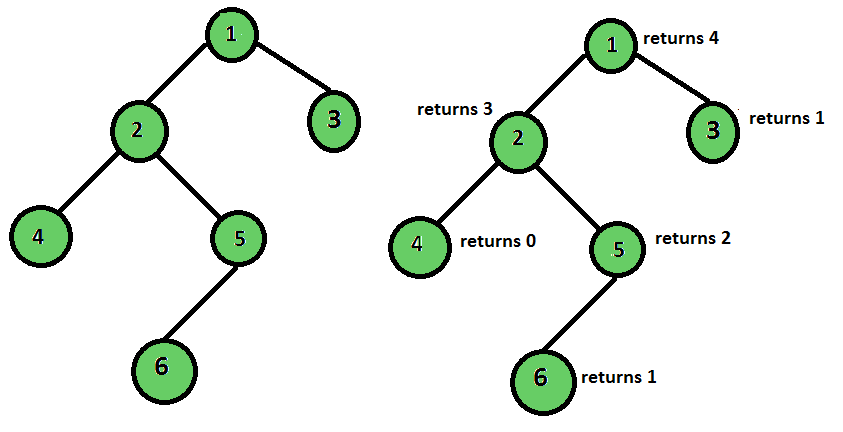
Output: Height of the tree is 4 

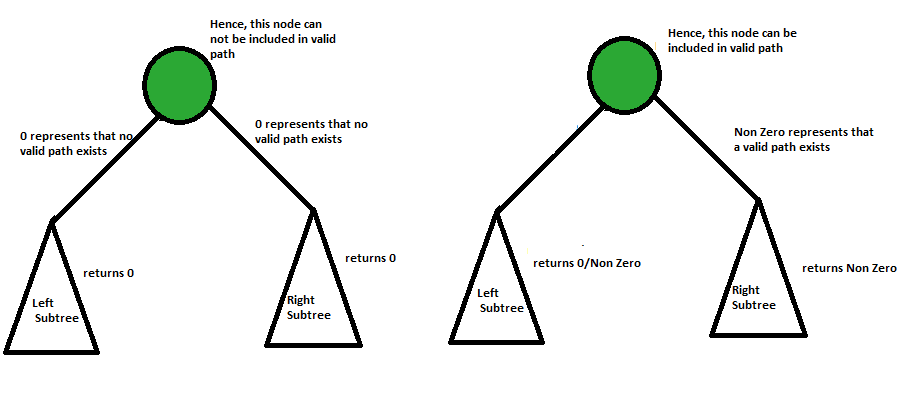
Approach: The approach to this problem is slightly different from the normal height finding approach. In the return step, we check if the node is a valid root node or not. If it is valid, return 1, else we return 0. Now in the recursive step- if the left and the right sub-tree both yield 0, the current node yields 0 too because in that case there is no path from the current node to a valid leaf node. But in the case at least one of the values returned by the children is non-zero, it means the leaf node on that path is a valid leaf node, and hence that path can contribute to the final result, so we return the max of the values returned + 1 for the current node. 

C++

/* Program to find height of the tree considering
   only even level leaves. */
#include <bits/stdc++.h>
using namespace std;

/* A binary tree node has data, pointer to
   left child and a pointer to right child */
struct Node {
    int data;
    struct Node* left;
    struct Node* right;
};

int heightOfTreeUtil(Node* root, bool isEven)
{
    // Base Case
    if (!root)
        return 0;

    if (!root->left && !root->right) {
        if (isEven)
            return 1;
        else
            return 0;
    }

    /*left stores the result of left subtree,
      and right stores the result of right subtree*/
    int left = heightOfTreeUtil(root->left, !isEven);
    int right = heightOfTreeUtil(root->right, !isEven);

    /*If both left and right returns 0, it means
      there is no valid path till leaf node*/
    if (left == 0 && right == 0)
        return 0;

    return (1 + max(left, right));
}

/* Helper function that allocates a new node with the
   given data and NULL left and right pointers. */
struct Node* newNode(int data)
{
    struct Node* node =
              (struct Node*)malloc(sizeof(struct Node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;

    return (node);
}

int heightOfTree(Node* root)
{
    return heightOfTreeUtil(root, false);
}

/* Driver program to test above functions*/
int main()
{
    // Let us create binary tree shown in above diagram
    struct Node* root = newNode(1);

    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    root->left->right->left = newNode(6);
    cout << "Height of tree is " << heightOfTree(root);
    return 0;
}

Java

/* Java Program to find height of the tree considering
only even level leaves. */
class GfG {

/* A binary tree node has data, pointer to
left child and a pointer to right child */
static class Node {
    int data;
    Node left;
 Node right;
}

static int heightOfTreeUtil(Node root, boolean isEven)
{
    // Base Case
    if (root == null)
        return 0;

    if (root.left == null && root.right == null) {
        if (isEven == true)
            return 1;
        else
            return 0;
    }

    /*left stores the result of left subtree,
    and right stores the result of right subtree*/
    int left = heightOfTreeUtil(root.left, !isEven);
    int right = heightOfTreeUtil(root.right, !isEven);

    /*If both left and right returns 0, it means
    there is no valid path till leaf node*/
    if (left == 0 && right == 0)
        return 0;

    return (1 + Math.max(left, right));
}

/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
static Node newNode(int data)
{
    Node node = new Node();
    node.data = data;
    node.left = null;
    node.right = null;

    return (node);
}

static int heightOfTree(Node root)
{
    return heightOfTreeUtil(root, false);
}

/* Driver program to test above functions*/
public static void main(String[] args)
{
    // Let us create binary tree shown in above diagram
    Node root = newNode(1);

    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);
    root.left.right.left = newNode(6);
    System.out.println("Height of tree is " + heightOfTree(root));
}
}

Python3

# Program to find height of the tree considering
# only even level leaves.

# Helper class that allocates a new node with the
# given data and None left and right pointers.
class newNode:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

def heightOfTreeUtil(root, isEven):

    # Base Case
    if (not root):
        return 0

    if (not root.left and not root.right):
        if (isEven):
            return 1
        else:
            return 0

    # left stores the result of left subtree,
    # and right stores the result of right subtree
    left = heightOfTreeUtil(root.left, not isEven)
    right = heightOfTreeUtil(root.right, not isEven)

    #If both left and right returns 0, it means
    # there is no valid path till leaf node
    if (left == 0 and right == 0):
        return 0

    return (1 + max(left, right))

def heightOfTree(root):
    return heightOfTreeUtil(root, False)

# Driver Code
if __name__ == '__main__':

    # Let us create binary tree shown
    # in above diagram
    root = newNode(1)

    root.left = newNode(2)
    root.right = newNode(3)
    root.left.left = newNode(4)
    root.left.right = newNode(5)
    root.left.right.left = newNode(6)
    print("Height of tree is",
           heightOfTree(root))

# This code is contributed by PranchalK

C#

/* C# Program to find height of the tree considering
only even level leaves. */
using System;

class GfG
{

    /* A binary tree node has data, pointer to
    left child and a pointer to right child */
    class Node
    {
        public int data;
        public Node left;
        public Node right;
    }

    static int heightOfTreeUtil(Node root,
                               bool isEven)
    {
        // Base Case
        if (root == null)
            return 0;

        if (root.left == null &&
            root.right == null)
        {
            if (isEven == true)
                return 1;
            else
                return 0;
        }

        /*left stores the result of left subtree,
        and right stores the result of right subtree*/
        int left = heightOfTreeUtil(root.left, !isEven);
        int right = heightOfTreeUtil(root.right, !isEven);

        /*If both left and right returns 0, it means
        there is no valid path till leaf node*/
        if (left == 0 && right == 0)
            return 0;

        return (1 + Math.Max(left, right));
    }

    /* Helper function that allocates a new node with the
    given data and NULL left and right pointers. */
    static Node newNode(int data)
    {
        Node node = new Node();
        node.data = data;
        node.left = null;
        node.right = null;

        return (node);
    }

    static int heightOfTree(Node root)
    {
        return heightOfTreeUtil(root, false);
    }

    /* Driver code*/
    public static void Main(String[] args)
    {
        // Let us create binary tree
        // shown in above diagram
        Node root = newNode(1);

        root.left = newNode(2);
        root.right = newNode(3);
        root.left.left = newNode(4);
        root.left.right = newNode(5);
        root.left.right.left = newNode(6);
        Console.WriteLine("Height of tree is " +
                            heightOfTree(root));
    }
}

/* This code is contributed by Rajput-Ji*/

Javascript

<script>
/* javascript Program to find height of the tree considering
only even level leaves. */

    /*
     * A binary tree node has data, pointer to left child and a pointer to right
     * child
     */

     class Node {
            constructor(val) {
                this.data = val;
                this.left = null;
                this.right = null;
            }
        }

    function heightOfTreeUtil(root,  isEven) {
        // Base Case
        if (root == null)
            return 0;

        if (root.left == null && root.right == null) {
            if (isEven == true)
                return 1;
            else
                return 0;
        }

        /*
         * left stores the result of left subtree, and right stores the result of right
         * subtree
         */
        var left = heightOfTreeUtil(root.left, !isEven);
        var right = heightOfTreeUtil(root.right, !isEven);

        /*
         * If both left and right returns 0, it means there is no valid path till leaf
         * node
         */
        if (left == 0 && right == 0)
            return 0;

        return (1 + Math.max(left, right));
    }

    /*
     * Helper function that allocates a new node with the given data and NULL left
     * and right pointers.
     */
    function newNode(data) {
var node = new Node();
        node.data = data;
        node.left = null;
        node.right = null;

        return (node);
    }

    function heightOfTree(root) {
        return heightOfTreeUtil(root, false);
    }

    /* Driver program to test above functions */

        // Let us create binary tree shown in above diagram
var root = newNode(1);

        root.left = newNode(2);
        root.right = newNode(3);
        root.left.left = newNode(4);
        root.left.right = newNode(5);
        root.left.right.left = newNode(6);
        document.write("Height of tree is " + heightOfTree(root));

// This code is contributed by umadevi9616
</script>

Output

Height of tree is 4

Time Complexity: O(n), Where n is the number of nodes in a given binary tree. 
Auxiliary Space: O(n), If we don’t consider the size of the recursive call stack for function calls then O(1), otherwise O(n).