Tree with N nodes and K leaves such that distance between farthest leaves is minimized
Last Updated :
07 Sep, 2022
Given N and K, print a tree such that the tree has no more than K leaf nodes and every other node has at least two nodes connected to it. The task is to build a tree of N nodes exactly in such a way that the distance between the farthest leaf nodes is minimized. Print the minimized distance also.
Note: There can be multiple trees.
Examples:
Input: N = 5, K = 3
Output: Distance = 3
The tree is:
1 2
2 3
3 4
3 5

Input: N = 3, K = 2
Output: Distance = 2
The tree is:
1 2
2 3
Approach:
- Initially, the tree will have k-1 nodes connected to 1.
- Then connect one node to all the k-1 nodes one by one.
- If nodes are left, keep connecting them to the leaf nodes one by one.
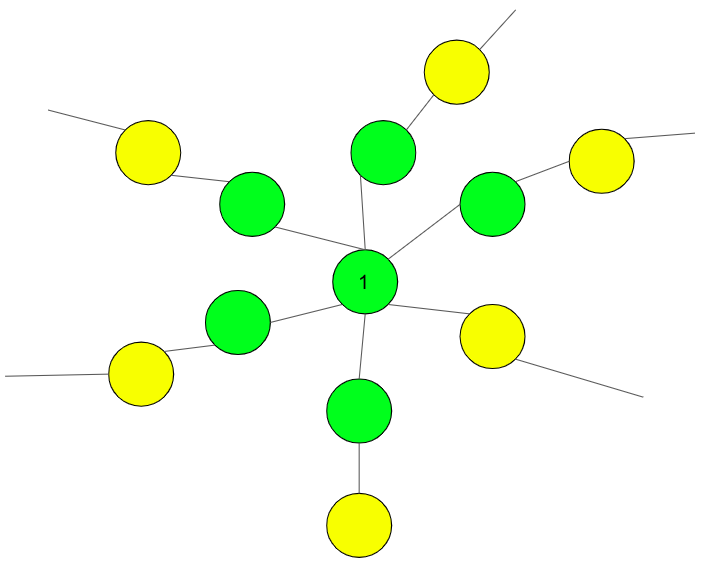
The diagrammatic representation of how to build the tree will make things more clear. In the image below, K = 6 and for any number N has been demonstrated. The nodes in yellow are the leaf nodes.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void buildTree(int n, int k)
{
int ans = 2 * ((n - 1) / k) + min((n - 1) % k, 2);
cout << "Distance = " << ans;
cout << "\nThe tree is:\n";
for (int i = 2; i <= k; i++) {
cout << "1 " << i << endl;
}
for (int i = k + 1; i <= n; i++) {
cout << i << " " << (i - k) << endl;
}
}
int main()
{
int n = 5, k = 3;
buildTree(n, k);
}
|
Java
import java.util.*;
import java.lang.*;
class GFG
{
public void buildTree(int n, int k)
{
int ans = 2 * ((n - 1) / k) +
Math.min((n - 1) % k, 2);
System.out.println("Distance = " + ans);
System.out.println("The tree is: ");
for (int i = 2; i <= k; i++)
{
System.out.println( "1 " + i );
}
for (int i = k + 1; i <= n; i++)
{
System.out.println( i + " " +
(i - k));
}
}
public static void main(String args[])
{
GFG g = new GFG();
int n = 5, k = 3;
g.buildTree(n, k);
}
}
|
Python3
def buildTree(n, k):
ans = (2 * ((n - 1) // k) +
min((n - 1) % k, 2))
print("Distance = ", ans )
print("The tree is:")
for i in range(2, k + 1):
print("1 ", i)
for i in range(k + 1, n + 1):
print(i, "", (i - k))
if __name__ == '__main__':
n = 5
k = 3
buildTree(n, k)
|
C#
using System;
class GFG
{
public void buildTree(int n, int k)
{
int ans = 2 * ((n - 1) / k) +
Math.Min((n - 1) % k, 2);
Console.WriteLine("Distance = " + ans);
Console.WriteLine ("The tree is: ");
for (int i = 2; i <= k; i++)
{
Console.WriteLine( "1 " + i );
}
for (int i = k + 1; i <= n; i++)
{
Console.WriteLine ( i + " " +
(i - k));
}
}
public static void Main()
{
GFG g = new GFG();
int n = 5, k = 3;
g.buildTree(n, k);
}
}
|
PHP
<?php
function buildTree($n, $k)
{
$ans = (2 * (int)(($n - 1) / $k) +
min(($n - 1) % $k, 2));
echo "Distance = " . $ans;
echo "\nThe tree is:\n";
for ($i = 2; $i <= $k; $i++)
{
echo "1 " . $i . "\n";
}
for ($i = $k + 1; $i <= $n; $i++)
{
echo $i . " " . ($i - $k) . "\n";
}
}
$n = 5; $k = 3;
buildTree($n, $k);
?>
|
Javascript
<script>
function buildTree(n , k)
{
var ans = parseInt(2 * ((n - 1) / k) + Math.min((n - 1) % k, 2));
document.write("Distance = " + ans+ "<br/>");
document.write("The tree is:<br/> ");
for (i = 2; i <= k; i++) {
document.write("1 " + i+"<br/>");
}
for (i = k + 1; i <= n; i++) {
document.write(i + " " + (i - k)+"<br/>");
}
}
var n = 5, k = 3;
buildTree(n, k);
</script>
|
Output
Distance = 3
The tree is:
1 2
1 3
4 1
5 2
Complexity Analysis:
- Time Complexity: O(n)
- As we are using traversing from i = 2 to i = n in the above two loops.
- Auxiliary Space: O(1)
- As constant extra space is used.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...