Different measures of central tendency are available to locate the centre of a data set. These include Arithmetic Mean, Median, Mode, Geometric Mean, and Harmonic Mean. Each of these measures is unique in its own way and has some characteristics.
What is Geometric Mean?
Geometric Mean or G.M. is a specialised average used in various specific areas and is defined as the nth root of the product of n values of a data set.
For Ungrouped Data:
The Geometric Mean of a data set with n observations as X1, X2, X3, X4, ……………Xn, is:
![Rendered by QuickLaTeX.com G.M.=\sqrt[n]{X_1\times{X_2}\times{X_3}\times{X_4}\times.......X_n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c18c2cb38c65ae65e86aee6e6cd8ff37_l3.png)
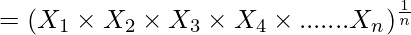
For instance, if n = 3; i.e., there are only 3 observations in a data set; say, 4, 5, and 6. Then the Geometric Mean of this data set will be 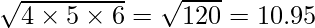
However, if the number of observations (n) is more than 3, then it will be difficult and time-consuming to determine the nth root. In these cases, to make the calculations simpler, we use logarithms; i.e., by taking log on both sides of the above formula, we get:
log (GM) = 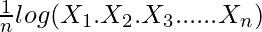
log (G.M.) = 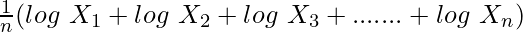
log (G.M.) = 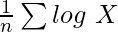
Now taking Antilog on both sides, we get:
G.M. = ![Rendered by QuickLaTeX.com Antilog[\frac{1}{n}\sum{log~X}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9a2b42ebe0471213b5264b2cea0de30f_l3.png)
Example:
Determine the Geometric Mean of the following data:
Solution:
log (G.M.) = 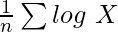
G.M. = ![Rendered by QuickLaTeX.com Antilog[\frac{1}{n}\sum{log~X}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9a2b42ebe0471213b5264b2cea0de30f_l3.png)
By taking log of each value of X, we get:
|
6
| 0.7782
|
10
| 1
|
7
| 0.8451
|
9
| 0.9542
|
8
| 0.9031
|
11
| 1.0414
|
12
| 1.0792
|
7
| 0.8451
|
Total
| 7.4463
|
G.M. = ![Rendered by QuickLaTeX.com Antilog[\frac{1}{n}\sum{log~X}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9a2b42ebe0471213b5264b2cea0de30f_l3.png)
= ![Rendered by QuickLaTeX.com Antilog[\frac{7.4463}{8}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-97be58baf5450f7ca4c528cfcd5dd2b8_l3.png)
= Antilog 0.93078
G.M. = 8.52
For Frequency Distribution:
In the case of discrete and continuous frequency distribution, the following method is used to determine the Geometric Mean:
- Determine the log values of X or mid-points in case of continuous distributions.
- Multiply the values of log X with their respective frequencies and calculate the sum of these products to get ∑f log X.
- Divide the value obtained by ∑f and take Antilog of the resultant figure to determine G.M.
Thus, the formula for calculating the Geometric Mean in the case of frequency distribution is:
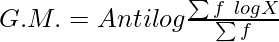
Example:
Calculate Geometric Mean of the following distribution.
|
0-10
| 5
|
10-20
| 10
|
20-30
| 8
|
30-40
| 4
|
40-50
| 1
|
50-60
| 2
|
Solution:
|
0-10
| 5
| 5
| 0.6990
| 3.495
|
10-20
| 15
| 10
| 1.1760
| 11.760
|
20-30
| 25
| 8
| 1.3980
| 11.184
|
30-40
| 35
| 4
| 1.5440
| 6.176
|
40-50
| 45
| 1
| 1.6532
| 1.6532
|
50-60
| 55
| 2
| 1.7403
| 3.4806
|
Total
|
| 30
|
| 37.7488
|
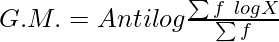
G.M. = ![Rendered by QuickLaTeX.com Antilog[\frac{37.7488}{30}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cf88f8f6caa5f1a4a963c51bee52d9d5_l3.png)
G.M. = Antilog 1.2582
G.M. = 18.125
Weighted Geometric Mean
In case different values of a data set are assigned weights, Weighted Geometric Mean is calculated. It is almost the same as Geometric Mean, the only difference is that frequency (f) is replaced by weights (W). Therefore, the formula for calculating Weighted Geometric Mean is,
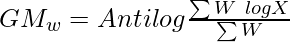
Example:
Calculate Weighted Geometric Mean of the following data:
2
| 4
| 6
| 8
| 10
| 12
| 14
|
2
| 5
| 4
| 3
| 1
| 4
| 1
|
Solution:
|
2
| 2
| 0.3010
| 0.602
|
4
| 5
| 0.6020
| 3.01
|
6
| 4
| 0.7781
| 3.1124
|
8
| 3
| 0.9030
| 2.709
|
10
| 1
| 1
| 1
|
12
| 4
| 1.0791
| 4.3164
|
14
| 1
| 1.1461
| 1.1461
|
Total
| 20
|
| 15.896
|
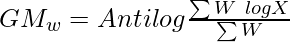
= ![Rendered by QuickLaTeX.com Antilog[\frac{15.896}{20}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f27dc5c63d397ffa82b0a812edfa0720_l3.png)
= Antilog 0.7948
G.M. = 6.23
Note: It should be kept in mind that if any value of the given data set is negative or zero, then the value of Geometric Mean cannot be calculated. Also, if the given data set is open-ended distribution, the value of Geometric Mean cannot be obtained because to determine G.M., the X values of all class intervals are required.
Properties of Geometric Mean
Different algebraic properties of Geometric Mean are as follows:
1. The product of n values is the same as the product obtained by replacing each value with its geometric mean. Simply put,
X1 x X2 x X3 x X4 x ……….. x Xn = (GM)n
For example, the geometric mean of 4, 8, 4, and 2 is equal to ![Rendered by QuickLaTeX.com \sqrt[4]{4\times{8}\times{4}\times{2}}=4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2fd4405c281662181cb563d3271da24f_l3.png)
Also, the product of the values; 4, 8, 4, and 2 is 256 which is equal to 44.
2. The product of the proportions of values lesser than or equal to the geometric mean to the geometric mean is equal to the product of the proportions of the geometric mean to the values greater than the geometric mean. Simply put,
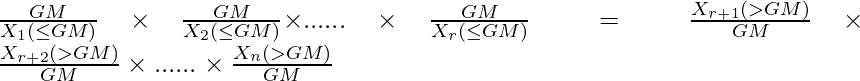
Taking the previous example into consideration, the values less than or equal to the geometric mean are 4, 4, and 2; and the value greater than the geometric mean is 8. Now,
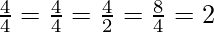
3. If the number of observations and geometric mean of two or more series are given, then their geometric mean can be determined. The formula of calculating combined geometric mean of two series is as follows:
Combined Geometric Mean = 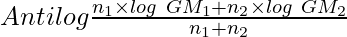
For example, the geometric mean of a set of 10 observations is 18.5 and the geometric mean of another set of 15 observations is 7.8. The combined geometric mean of both the sets will be,
Combined Geometric Mean = 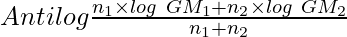
= 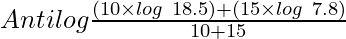
= 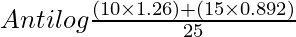
= Antilog 1.0392
Combined Geometric Mean = 10.94
Uses of Geometric Mean
If the quantities required for the average are drawn from the situations where the exponential law of growth (or decline) is used, then Geometric Mean would be an appropriate measure to use. For example, growth of population, deposits in a bank account attracting compound interest, depreciation charged using diminishing balance method, etc. Geometric Mean is used in these cases to determine the average percentage rates of increase or decrease from the given yearly change or other periodic change. It is also used to average the ratios.
For a better understanding of the concept, let’s take the formula of compound interest in which a sum P carries an interest rate (r) per time period, and becomes an amount (A) in n time periods:
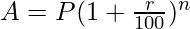
Now, by algebraically manipulating the above formula, we can get the value of r as:
![Rendered by QuickLaTeX.com r=[\sqrt[n]{A/P}]\times{100}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-84e050071a048fbbaeefe282c1274715_l3.png)
This formula can be used to calculate the percentage rate of interest per unit of time, where initial value (P), end value (A), and number of time periods (n) are given.
Besides, this relationship can be used in both conditions; when the interest rate (r) is uniform, or when the interest rate varies. For example, suppose a three-year deposit in a bank attracts r1, r2, and r3 percent per annum interest rate in the years 1, 2, and 3 respectively. Then, the average interest rate (r) can be determined as:
Given: 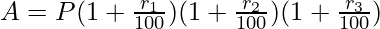 and n = 3
and n = 3
Therefore,
![Rendered by QuickLaTeX.com r=[\sqrt[3]{\frac{P(\frac{100+r_1}{100})(\frac{100+r_2}{100})(\frac{100+r_3}{100})}{P}}-1]\times{100}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-70d3931dbcf2b9bb802695b47341075a_l3.png)
r = [(100 + r1)(100 + r2)(100 + r3)]1/3 – 100
Alternatively,
r = GM[(100 + r1, 100 + r2, 100 + r3)]-100
Therefore, we can easily determine the average rate of interest with the help of Geometric Mean.
Example:
The percentage increase in the net worth of a company over the last 6 years is given below. Determine the average percentage increase in the net worth of the company over the 6-year period.
2018
| 2019
| 2020
| 2021
| 2022
| 2023
|
5.0
| 3.4
| 7.5
| 4.8
| 2.6
| 1.8
|
Solution:
By using Geometric Mean, we can calculate the average percentage increase in the net worth of the company over the 6-year period.
|
2018
| 5.0
| 105.0
| 2.0211
|
2019
| 3.4
| 103.4
| 2.0145
|
2020
| 7.5
| 107.5
| 2.0314
|
2021
| 4.8
| 104.8
| 2.0203
|
2022
| 2.6
| 102.6
| 2.0111
|
2023
| 1.8
| 101.8
| 2.0077
|
|
| Total
| 12.1061
|
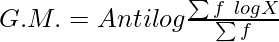
G.M. = 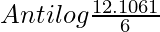
G.M. = Antilog 2.01768
G.M. = 104.15
Now,
Average percentage increase in net worth = 104.15 – 100
Average percentage increase in net worth = 4.15 per annum
Share your thoughts in the comments
Please Login to comment...