Game Theory in Balanced Ternary Numeral System | (Moving 3k steps at a time)
Last Updated :
03 Aug, 2022
Just like base 2 Binary numeral system having 0s and 1s as digits, Ternary(Trinary) Numeral System is a base 3 number system having 0s, 1s and -1 as digits.
It’s better to use alphabet ‘Z’ in place of -1, since while denoting full ternary number -1 looks odd in between 1s and 0s.
Conversion of decimal into Balanced Ternary:
As in binary conversion, first represent the decimal number into the normal ternary system having 0, 1, 2 as reminders.
Now Iterating from the lowest digit safely skip any 0s and 1s, however turn 2 into Z and add 1 to the next digit. Turn 3 into 0 on the same terms( such digits are not present in the number initially but they can be encountered after increasing some 2s. )
Examples:
Decimal: 128
Ternary: 11202
Balanced Ternary: 1ZZZ1Z
Decimal: 1000
Ternary: 1102101
Balanced Ternary: 111Z101
C++
#include <bits/stdc++.h>
using namespace std;
int arr[32];
void balTernary(int ter)
{
int carry = 0, base = 10;
int i = 32;
while (ter > 0) {
int rem = ter % base;
rem = rem + carry;
if (rem == 0) {
arr[i--] = 0;
carry = 0;
}
else if (rem == 1) {
arr[i--] = 1;
carry = 0;
}
else if (rem == 2) {
arr[i--] = -1;
carry = 1;
}
else if (rem == 3) {
arr[i--] = 0;
carry = 1;
}
ter = ter / base;
}
if (carry == 1)
arr[i] = 1;
}
int ternary(int number)
{
int ans = 0, rem = 1, base = 1;
while (number > 0) {
rem = number % 3;
ans = ans + rem * base;
number /= 3;
base = base * 10;
}
return ans;
}
int main()
{
int number = 3056;
int ter = ternary(number);
memset(arr, 0, sizeof(arr));
balTernary(ter);
int i = 0;
while (arr[i] == 0) {
i++;
}
for (int j = i; j <= 32; j++) {
if (arr[j] == -1)
cout << 'Z';
else
cout << arr[j];
}
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int []arr = new int[33];
static void balTernary(int ter)
{
int carry = 0, base = 10;
int i = 32;
while (ter > 0)
{
int rem = ter % base;
rem = rem + carry;
if (rem == 0)
{
arr[i--] = 0;
carry = 0;
}
else if (rem == 1)
{
arr[i--] = 1;
carry = 0;
}
else if (rem == 2)
{
arr[i--] = -1;
carry = 1;
}
else if (rem == 3)
{
arr[i--] = 0;
carry = 1;
}
ter = (int)(ter / base);
}
if (carry == 1)
arr[i] = 1;
}
static int ternary(int number)
{
int ans = 0, rem = 1, base = 1;
while (number > 0)
{
rem = number % 3;
ans = ans + rem * base;
number = (int)(number/3);
base = base * 10;
}
return ans;
}
public static void main(String args[])
{
int number = 3056;
int ter = ternary(number);
Arrays.fill(arr,0);
balTernary(ter);
int i = 0;
while (arr[i] == 0)
{
i++;
}
for (int j = i; j <= 32; j++)
{
if (arr[j] == -1)
System.out.print('Z');
else
System.out.print(arr[j]);
}
}
}
|
Python3
arr = [0] * 32
def balTernary(ter):
carry, base, i = 0, 10, 31
while ter > 0:
rem = (ter % base) + carry
if rem == 0:
arr[i] = 0
carry, i = 0, i-1
elif rem == 1:
arr[i] = 1
carry, i = 0, i-1
elif rem == 2:
arr[i] = -1
carry, i = 1, i-1
elif rem == 3:
arr[i] = 0
carry, i = 1, i-1
ter = ter // base
if carry == 1:
arr[i] = 1
def ternary(number):
ans, rem, base = 0, 1, 1
while number > 0:
rem = number % 3
ans = ans + rem * base
number //= 3
base = base * 10
return ans
if __name__ == "__main__":
number = 3056
ter = ternary(number)
balTernary(ter)
i = 0
while arr[i] == 0:
i += 1
for j in range(i, 32):
if arr[j] == -1:
print('Z', end = "")
else:
print(arr[j], end = "")
|
C#
using System;
class GFG
{
static int []arr = new int[33];
static void balTernary(int ter)
{
int carry = 0, b = 10;
int i = 32;
while (ter > 0)
{
int rem = ter % b;
rem = rem + carry;
if (rem == 0)
{
arr[i--] = 0;
carry = 0;
}
else if (rem == 1)
{
arr[i--] = 1;
carry = 0;
}
else if (rem == 2)
{
arr[i--] = -1;
carry = 1;
}
else if (rem == 3)
{
arr[i--] = 0;
carry = 1;
}
ter = (int)(ter / b);
}
if (carry == 1)
arr[i] = 1;
}
static int ternary(int number)
{
int ans = 0, rem = 1, b = 1;
while (number > 0)
{
rem = number % 3;
ans = ans + rem * b;
number = (int)(number / 3);
b = b * 10;
}
return ans;
}
public static void Main(String []args)
{
int number = 3056;
int ter = ternary(number);
balTernary(ter);
int i = 0;
while (arr[i] == 0)
{
i++;
}
for (int j = i; j <= 32; j++)
{
if (arr[j] == -1)
Console.Write('Z');
else
Console.Write(arr[j]);
}
}
}
|
Javascript
<script>
let arr = new Array(33);
function balTernary(ter)
{
let carry = 0, base = 10;
let i = 32;
while (ter > 0)
{
let rem = ter % base;
rem = rem + carry;
if (rem == 0)
{
arr[i--] = 0;
carry = 0;
}
else if (rem == 1)
{
arr[i--] = 1;
carry = 0;
}
else if (rem == 2)
{
arr[i--] = -1;
carry = 1;
}
else if (rem == 3)
{
arr[i--] = 0;
carry = 1;
}
ter = Math.floor(ter / base);
}
if (carry == 1)
arr[i] = 1;
}
function ternary(number)
{
let ans = 0, rem = 1, base = 1;
while (number > 0)
{
rem = number % 3;
ans = ans + rem * base;
number = Math.floor(number/3);
base = base * 10;
}
return ans;
}
let number = 3056;
let ter = ternary(number);
for(let i=0;i<arr.length;i++)
{
arr[i]=0;
}
balTernary(ter);
let i = 0;
while (arr[i] == 0)
{
i++;
}
for (let j = i; j <= 32; j++)
{
if (arr[j] == -1)
document.write('Z');
else
document.write(arr[j]);
}
</script>
|
Time Complexity: O(log3n) as the time is constant.
Auxiliary Space: O(1)
Recovering original decimal number from a balanced ternary number:-
Procedure:- Similarly as it’s done in binary to decimal conversion
Example:- 111ZZ1ZZ
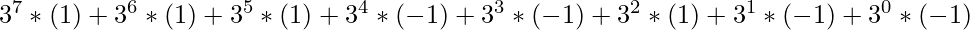
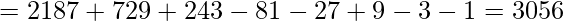
Game Rules:
There are two robots allowed to move in steps on x-axis starting from 0.
They can make several steps starting from 0 but there are some limitations on their movement.
In 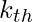 step robot will move exact
step robot will move exact 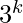 units of distance.
units of distance.
In each step robot must choose one of the two directions left (x- coordinate decreases) or right (x-coordinate increases), in a particular step only one robot will move and another will wait.
It is not allowed to skip any step.
Statement:
Given two integers x1 and x2. Robot 1 and 2 are separately required to cover their respective distances x1 and x2. Is it possible??
If it is possible you won otherwise you lose.
Approach:
There is only one balanced ternary representation of each Decimal number (distance here), this means there is only one way to cover a particular distance satisfying above rules.
So, if it is possible to cover distances x1 and x2 such that when one robot moves other remains still and both can’t remain still at the same time then it’s a victory.
Logic:
First represent x1 and x2 as balanced ternary number using above procedure.
Iterate from LSB check:-
At a time(step) only one value should be 1 or Z.
Both can’t be 0 at the same time(step).
If rule breaks at any step it’s your lose otherwise you won.
Example:
Input: x1 = 6890, x2 = 18252
Output:
Balanced ternary representation of x1 = 01001101ZZ
Balanced ternary representation of x2 = 10Z1001000
Victory
Input: x1 = 18, x2 = 45
Output:
Balanced ternary representation of x1 = 01Z00
Balanced ternary representation of x2 = 1ZZ00
Defeat
Iterate bitwise over both the arrays and break wherever rule breaks.
To do first make length of both arrays equal by adding 0s at beginning of the shortest one, such that length becomes same.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isDefeat(string s1, string s2, int n)
{
for (int i = 0; i < n; i++) {
if ((s1[i] == '0' && s2[i] == '1')
|| (s1[i] == '1' && s2[i] == '0'))
continue;
else if ((s1[i] == '0' && s2[i] == 'Z')
|| (s1[i] == 'Z' && s2[i] == '0'))
continue;
else {
return true;
}
}
return false;
}
int main()
{
string s1 = { "01001101ZZ" };
string s2 = { "10Z1001000" };
int n = 10;
if (isDefeat(s1, s2, n))
cout << "Defeat";
else
cout << "Victory";
return 0;
}
|
Java
class GfG
{
static boolean isDefeat(String s1, String s2, int n)
{
for (int i = 0; i < n; i++)
{
if ((s1.charAt(i) == '0' && s2.charAt(i) == '1')
|| (s1.charAt(i) == '1' && s2.charAt(i) == '0'))
continue;
else if ((s1.charAt(i) == '0' && s2.charAt(i) == 'Z')
|| (s1.charAt(i) == 'Z' && s2.charAt(i) == '0'))
continue;
else
{
return true;
}
}
return false;
}
public static void main(String[] args)
{
String s1 = ("01001101ZZ" );
String s2 = ("10Z1001000" );
int n = 10;
if (isDefeat(s1, s2, n))
System.out.println("Defeat");
else
System.out.println("Victory");
}
}
|
Python3
def isDefeat(s1, s2, n):
for i in range(n):
if ((s1[i] == '0' and s2[i] == '1') or
(s1[i] == '1' and s2[i] == '0')):
continue
elif ((s1[i] == '0' and s2[i] == 'Z') or
(s1[i] == 'Z' and s2[i] == '0')):
continue
else:
return True
return False
s1 = "01001101ZZ"
s2 = "10Z1001000"
n = 10
if (isDefeat(s1, s2, n)):
print("Defeat")
else:
print("Victory")
|
C#
using System;
class GfG
{
static bool isDefeat(string s1, string s2, int n)
{
for (int i = 0; i < n; i++)
{
if ((s1[i] == '0' && s2[i] == '1')
|| (s1[i] == '1' && s2[i] == '0'))
continue;
else if ((s1[i] == '0' && s2[i] == 'Z')
|| (s1[i] == 'Z' && s2[i]== '0'))
continue;
else
{
return true;
}
}
return false;
}
public static void Main()
{
string s1 = ("01001101ZZ" );
string s2 = ("10Z1001000" );
int n = 10;
if (isDefeat(s1, s2, n))
Console.WriteLine("Defeat");
else
Console.WriteLine("Victory");
}
}
|
PHP
<?php
function isDefeat($s1, $s2, $n)
{
for ($i = 0; $i < $n; $i++)
{
if( ($s1[$i] == '0' && $s2[$i] == '1')
|| ($s1[$i] == '1' && $s2[$i] == '0'))
continue;
else if (($s1[$i] == '0' && $s2[$i] == 'Z')
|| ($s1[$i] == 'Z' && $s2[$i] == '0'))
continue;
else
{
return true;
}
}
return false;
}
$s1 = ("01001101ZZ" );
$s2 = ("10Z1001000" );
$n = 10;
if (isDefeat($s1, $s2, $n))
echo("Defeat");
else
echo("Victory");
|
Javascript
<script>
function isDefeat(s1, s2, n)
{
for(let i = 0; i < n; i++)
{
if ((s1[i] == '0' && s2[i] == '1') ||
(s1[i] == '1' && s2[i] == '0'))
continue;
else if ((s1[i] == '0' && s2[i] == 'Z') ||
(s1[i] == 'Z' && s2[i]== '0'))
continue;
else
{
return true;
}
}
return false;
}
let s1 = ("01001101ZZ");
let s2 = ("10Z1001000");
let n = 10;
if (isDefeat(s1, s2, n))
document.write("Defeat");
else
document.write("Victory");
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...