Flatten a binary tree into linked list

Given a binary tree, flatten it into linked list in-place. Usage of auxiliary data structure is not allowed. After flattening, left of each node should point to NULL and right should contain next node in preorder.

Examples: 

Input : 
          1
        /   \
       2     5
      / \     \
     3   4     6

Output :
    1
     \
      2
       \
        3
         \
          4
           \
            5
             \
              6

Input :
        1
       / \
      3   4
         /
        2
         \
          5
Output :
     1
      \
       3
        \
         4
          \
           2
            \ 
             5

Simple Approach: A simple solution is to use Level Order Traversal using Queue. In level order traversal, keep track of previous node. Make current node as right child of previous and left of previous node as NULL. This solution requires queue, but question asks to solve without additional data structure.

Efficient Without Additional Data Structure Recursively look for the node with no grandchildren and both left and right child in the left sub-tree. Then store node->right in temp and make node->right=node->left. Insert temp in first node NULL on right of node by node=node->right. Repeat until it is converted to linked list. 

For Example, 

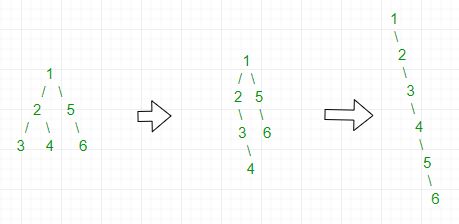
Implementation:

C++

// C++ Program to flatten a given Binary Tree into linked
// list by using Morris Traversal concept
#include <bits/stdc++.h>
using namespace std;

struct Node {
    int key;
    Node *left, *right;
};

// utility that allocates a new Node with the given key
Node* newNode(int key)
{
    Node* node = new Node;
    node->key = key;
    node->left = node->right = NULL;
    return (node);
}

// Function to convert binary tree into linked list by
// altering the right node and making left node point to
// NULL
void flatten(struct Node* root)
{
    // base condition- return if root is NULL or if it is a
    // leaf node
    if (root == NULL || root->left == NULL && root->right == NULL)
        return;
    // if root->left exists then we have to make it
    // root->right
    if (root->left != NULL) {
        // move left recursively
        flatten(root->left);
        // store the node root->right
        struct Node* tmpRight = root->right;
        root->right = root->left;
        root->left = NULL;
        // find the position to insert the stored value
        struct Node* t = root->right;
        while (t->right != NULL)
            t = t->right;
        // insert the stored value
        t->right = tmpRight;
    }
    // now call the same function for root->right
    flatten(root->right);
}

// To find the inorder traversal
void inorder(struct Node* root)
{
    // base condition
    if (root == NULL)
        return;
    inorder(root->left);
    cout << root->key << " ";
    inorder(root->right);
}

/* Driver program to test above functions*/
int main()
{
    /*    1
        /   \
       2     5
      / \     \
     3   4     6 */
    Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(5);
    root->left->left = newNode(3);
    root->left->right = newNode(4);
    root->right->right = newNode(6);
    flatten(root);
    cout << "The Inorder traversal after flattening binary tree ";
    inorder(root);
    return 0;
}

// This code is contributed by Aditya Kumar (adityakumar129)

C

// C Program to flatten a given Binary Tree into linked
// list
#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int key;
    struct Node *left, *right;
}Node;

// utility that allocates a new Node with the given key
Node* newNode(int key)
{
    Node* node = (Node*)malloc(sizeof(Node));
    node->key = key;
    node->left = node->right = NULL;
    return (node);
}

// Function to convert binary tree into linked list by
// altering the right node and making left node point to
// NULL
void flatten(Node* root)
{
    // base condition- return if root is NULL or if it is a
    // leaf node
    if (root == NULL || root->left == NULL && root->right == NULL)
        return;

    // if root->left exists then we have to make it
    // root->right
    if (root->left != NULL) {
        // move left recursively
        flatten(root->left);
        // store the node root->right
        struct Node* tmpRight = root->right;
        root->right = root->left;
        root->left = NULL;
        // find the position to insert the stored value
        struct Node* t = root->right;
        while (t->right != NULL)
            t = t->right;
        // insert the stored value
        t->right = tmpRight;
    }

    // now call the same function for root->right
    flatten(root->right);
}

// To find the inorder traversal
void inorder(struct Node* root)
{
    // base condition
    if (root == NULL)
        return;
    inorder(root->left);
    printf("%d ", root->key);
    inorder(root->right);
}

/* Driver program to test above functions*/
int main()
{
    /*    1
        /   \
       2     5
      / \     \
     3   4     6 */
    Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(5);
    root->left->left = newNode(3);
    root->left->right = newNode(4);
    root->right->right = newNode(6);

    flatten(root);

    printf("The Inorder traversal after flattening binary tree ");
    inorder(root);
    return 0;
}

// This code is contributed by aditykumar129.

Java

// Java program to flatten a given Binary Tree into linked
// list

// A binary tree node
class Node {
    int data;
    Node left, right;
    Node(int key)
    {
        data = key;
        left = right = null;
    }
}

class BinaryTree {

    Node root;

    // Function to convert binary tree into linked list by
    // altering the right node and making left node NULL
    public void flatten(Node node)
    {
        // Base case - return if root is NULL
        if (node == null)
            return;
        // Or if it is a leaf node
        if (node.left == null && node.right == null)
            return;
        // If root.left children exists then we have to make
        // it node.right (where node is root)
        if (node.left != null) {
            // Move left recursively
            flatten(node.left);
            // Store the node.right in Node named tempNode
            Node tempNode = node.right;
            node.right = node.left;
            node.left = null;
            // Find the position to insert the stored value
            Node curr = node.right;
            while (curr.right != null)
                curr = curr.right;
            // Insert the stored value
            curr.right = tempNode;
        }
        // Now call the same function for node.right
        flatten(node.right);
    }
    // Function for Inorder traversal
    public void inOrder(Node node)
    {
        // Base Condition
        if (node == null)
            return;
        inOrder(node.left);
        System.out.print(node.data + " ");
        inOrder(node.right);
    }

    // Driver code
    public static void main(String[] args)
    {
        BinaryTree tree = new BinaryTree();

        /*    1
            /   \
           2     5
          / \     \
         3   4     6 */

        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(5);
        tree.root.left.left = new Node(3);
        tree.root.left.right = new Node(4);
        tree.root.right.right = new Node(6);

        System.out.println(
            "The Inorder traversal after flattening binary tree ");
        tree.flatten(tree.root);
        tree.inOrder(tree.root);
    }
}

// This code is contributed by Aditya Kumar (adityakumar129)

Python3

# Python3 program to flatten a given Binary
# Tree into linked list
class Node:

    def __init__(self):

        self.key = 0
        self.left = None
        self.right = None

# Utility that allocates a new Node
# with the given key
def newNode(key):

    node = Node()
    node.key = key
    node.left = node.right = None
    return (node)

# Function to convert binary tree into
# linked list by altering the right node
# and making left node point to None
def flatten(root):

    # Base condition- return if root is None
    # or if it is a leaf node
    if (root == None or root.left == None and
                        root.right == None):
        return

    # If root.left exists then we have
    # to make it root.right
    if (root.left != None):

        # Move left recursively
        flatten(root.left)

        # Store the node root.right
        tmpRight = root.right
        root.right = root.left
        root.left = None

        # Find the position to insert
        # the stored value
        t = root.right
        while (t.right != None):
            t = t.right

        # Insert the stored value
        t.right = tmpRight

    # Now call the same function
    # for root.right
    flatten(root.right)

# To find the inorder traversal
def inorder(root):

    # Base condition
    if (root == None):
        return

    inorder(root.left)
    print(root.key, end = ' ')
    inorder(root.right)

# Driver Code
if __name__=='__main__':

    '''   1
        /   \
       2     5
      / \     \
     3   4     6 '''
    root = newNode(1)
    root.left = newNode(2)
    root.right = newNode(5)
    root.left.left = newNode(3)
    root.left.right = newNode(4)
    root.right.right = newNode(6)

    flatten(root)

    print("The Inorder traversal after "
          "flattening binary tree ",
          end = '')
    inorder(root)

# This code is contributed by pratham76

C#

// C# program to flatten a given
// Binary Tree into linked list
using System;

// A binary tree node
class Node
{
  public int data;
  public Node left, right;

  public Node(int key)
  {
    data = key;
    left = right = null;
  }
}

class BinaryTree
{
  Node root;

  // Function to convert binary tree into
  // linked list by altering the right node
  // and making left node NULL
  public void flatten(Node node)
  {

    // Base case - return if root is NULL
    if (node == null)
      return;

    // Or if it is a leaf node
    if (node.left == null &&
        node.right == null)
      return;

    // If root.left children exists then we have
    // to make it node.right (where node is root)
    if (node.left != null)
    {

      // Move left recursively
      flatten(node.left);

      // Store the node.right in
      // Node named tempNode
      Node tempNode = node.right;
      node.right = node.left;
      node.left = null;

      // Find the position to insert
      // the stored value
      Node curr = node.right;
      while (curr.right != null)
      {
        curr = curr.right;
      }

      // Insert the stored value
      curr.right = tempNode;
    }

    // Now call the same function
    // for node.right
    flatten(node.right);

  }

  // Function for Inorder traversal
  public void inOrder(Node node)
  {

    // Base Condition
    if (node == null)
      return;
    inOrder(node.left);
    Console.Write(node.data + " ");
    inOrder(node.right);
  }

  // Driver code
  public static void Main(string[] args)
  {
    BinaryTree tree = new BinaryTree();

    /* 1
        / \
    2     5
    / \     \
    3 4     6 */

    tree.root = new Node(1);
    tree.root.left = new Node(2);
    tree.root.right = new Node(5);
    tree.root.left.left = new Node(3);
    tree.root.left.right = new Node(4);
    tree.root.right.right = new Node(6);
    Console.Write("The Inorder traversal after " +
                  "flattening binary tree ");
    tree.flatten(tree.root);
    tree.inOrder(tree.root);
  }
}

// This code is contributed by rutvik_56

Javascript

<script>

// Javascript program to flatten a given
// Binary Tree into linked list

// A binary tree node
class Node
{
    constructor(key)
    {
        this.data = key;
        this.left = null;
        this.right = null;
    }
}

var root;

// Function to convert binary tree into
// linked list by altering the right node
// and making left node NULL
function flatten(node)
{

    // Base case - return if root is NULL
    if (node == null)
        return;

    // Or if it is a leaf node
    if (node.left == null &&
        node.right == null)
        return;

    // If root.left children exists then we have
    // to make it node.right (where node is root)
    if (node.left != null)
    {

        // Move left recursively
        flatten(node.left);

        // Store the node.right in
        // Node named tempNode
        var tempNode = node.right;
        node.right = node.left;
        node.left = null;

        // Find the position to insert
        // the stored value
        var curr = node.right;
        while (curr.right != null)
        {
            curr = curr.right;
        }

        // Insert the stored value
        curr.right = tempNode;
    }

    // Now call the same function
    // for node.right
    flatten(node.right);
}

// Function for Inorder traversal
function inOrder(node)
{

    // Base Condition
    if (node == null)
        return;

    inOrder(node.left);
    document.write(node.data + " ");
    inOrder(node.right);
}

// Driver code
/*   1
    / \
  2     5
 / \     \
3   4     6 */
root = new Node(1);
root.left = new Node(2);
root.right = new Node(5);
root.left.left = new Node(3);
root.left.right = new Node(4);
root.right.right = new Node(6);

document.write("The Inorder traversal after " +
               "flattening binary tree ");
flatten(root);
inOrder(root);

// This code is contributed by famously

</script>

Output

The Inorder traversal after flattening binary tree 1 2 3 4 5 6 

Complexity Analysis:

• Time Complexity: O(n), traverse the whole tree
• Space Complexity: O(1), No Extra Space is used

Another Approach:
We will use the intuition behind morris’s traversal. In Morris Traversal we use the concept of a threaded binary tree.

At a node(say cur) if there exists a left child, we will find the rightmost node in the left subtree(say prev).
We will set prev’s right child to cur’s right child,
We will then set cur’s right child to it’s left child.
We will then move cur to the next node by assigning cur it to its right child
We will stop the execution when cur points to NULL.

Implementation:

C++

// C++ Program to flatten a given Binary Tree into linked
// list
#include <bits/stdc++.h>
using namespace std;

struct Node {
    int key;
    Node *left, *right;
};

// utility that allocates a new Node with the given key
Node* newNode(int key)
{
    Node* node = new Node;
    node->key = key;
    node->left = node->right = NULL;
    return (node);
}

// Function to convert binary tree into linked list by
// altering the right node and making left node point to
// NULL
void flatten(Node* root)
{
    // traverse till root is not NULL
    while (root) {
        // if root->left is not NULL
        if (root->left != NULL) {
            // set curr node as root->left;
            Node* curr = root->left;
            // traverse to the extreme right of curr
            while (curr->right) {
                curr = curr->right;
            }
            // join curr->right to root->right
            curr->right = root->right;
            // put root->left to root->right
            root->right = root->left;
            // make root->left as NULL
            root->left = NULL;
        }
        // now go to the right of the root
        root = root->right;
    }
}

// To find the inorder traversal
void inorder(struct Node* root)
{
    // base condition
    if (root == NULL)
        return;
    inorder(root->left);
    cout << root->key << " ";
    inorder(root->right);
}

/* Driver program to test above functions*/
int main()
{
    /*    1
        /   \
       2     5
      / \     \
     3   4     6 */
    Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(5);
    root->left->left = newNode(3);
    root->left->right = newNode(4);
    root->right->right = newNode(6);
    flatten(root);
    cout << "The Inorder traversal after flattening binary "
            "tree ";
    inorder(root);
    return 0;
}

// This code is contributed by Harsh Raghav

Java

// Java Program to flatten a given Binary Tree into linked
// list
import java.io.*;

class Node {
  int key;
  Node left, right;
}

class GFG {

  // utility that allocates a new Node with the given key
  static Node newNode(int key)
  {
    Node node = new Node();
    node.key = key;
    node.left = node.right = null;
    return node;
  }

  // Function to convert binary tree into linked list by
  // altering the right node and making left node point to
  // NULL
  static void flatten(Node root)
  {
    // traverse till root is not NULL
    while (root != null) {
      // if root->left is not NULL
      if (root.left != null) {
        // set curr node as root->left;
        Node curr = root.left;
        // traverse to the extreme right of curr
        while (curr.right != null) {
          curr = curr.right;
        }
        // join curr->right to root->right
        curr.right = root.right;
        // put root->left to root->right
        root.right = root.left;
        // make root->left as NULL
        root.left = null;
      }
      // now go to the right of the root
      root = root.right;
    }
  }

  // To find the inorder traversal
  static void inorder(Node root)
  {
    // base condition
    if (root == null) {
      return;
    }
    inorder(root.left);
    System.out.print(root.key + " ");
    inorder(root.right);
  }

  public static void main(String[] args)
  {

    /*    1
            /   \
              2     5
            / \     \
          3   4     6  */

    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(5);
    root.left.left = newNode(3);
    root.left.right = newNode(4);
    root.right.right = newNode(6);
    flatten(root);

    System.out.print(
      "The Inorder traversal after flattening binary tree ");
    inorder(root);
  }
}

// This code is contributed by lokesh.

Output

The Inorder traversal after flattening binary tree 1 2 3 4 5 6 

Time Complexity: O(N) Time complexity will be the same as that of a Morris’s traversal
Auxiliary Space: O(1)