Find position of given term in a series formed with only digits 4 and 7 allowed
Last Updated :
08 Jun, 2022
There is a series of numbers that have only digits, 4 and 7, and numbers are arranged in increasing order. The first few numbers of the series are 4, 7, 44, 47, 74, 77, 444, …etc. Given a number N, the task is to find the position of that number in the given series.
Examples:
Input: N = 4
Output: 1
Explanation:
The first number in the series is 4
Input: N = 777
Output: 14
Explanation:
The 14th number in the series is 777
Approach: This problem can be solved using the below observations:
- Below is the pattern observe in the given series. The numbers can be seen as:
""
/ \
4 7
/ \ / \
44 47 74 77
/ \ / \ / \ / \
- As we can observe the pattern is increasing in power of 2. Therefore the idea is to iterate over the digits of the number starting from the least significant digit and update the position of the number as:
- If current digit = 7, then add
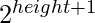 to the position.
to the position. - If current digit = 4, then add
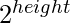 to the position.
to the position.
- Print the final position after the above operations.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findPosition(int n)
{
int i = 0;
int pos = 0;
while (n > 0) {
if (n % 10 == 7) {
pos = pos + pow(2, i + 1);
}
else {
pos = pos + pow(2, i);
}
i++;
n = n / 10;
}
cout << pos;
}
int main()
{
int N = 777;
findPosition(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void findPosition(int n)
{
int i = 0;
int pos = 0;
while (n > 0)
{
if (n % 10 == 7)
{
pos = pos + (int)Math.pow(2, i + 1);
}
else
{
pos = pos + (int)Math.pow(2, i);
}
i++;
n = n / 10;
}
System.out.print(pos);
}
public static void main(String[] args)
{
int N = 777;
findPosition(N);
}
}
|
Python3
def findPosition(n):
i = 0
pos = 0
while (n > 0):
if (n % 10 == 7):
pos = pos + pow(2, i + 1)
else:
pos = pos + pow(2, i)
i += 1
n = n // 10
print(pos)
if __name__ == '__main__':
N = 777
findPosition(N)
|
C#
using System;
class GFG{
static void findPosition(int n)
{
int i = 0;
int pos = 0;
while (n > 0)
{
if (n % 10 == 7)
{
pos = pos + (int)Math.Pow(2, i + 1);
}
else
{
pos = pos + (int)Math.Pow(2, i);
}
i++;
n = n / 10;
}
Console.Write(pos);
}
public static void Main()
{
int N = 777;
findPosition(N);
}
}
|
Javascript
<script>
function findPosition(n)
{
var i = 0;
var pos = 0;
while (n > 0) {
if (n % 10 == 7) {
pos = pos + parseInt( Math.pow(2, i + 1));
}
else {
pos = pos + parseInt( Math.pow(2, i));
}
i++;
n = parseInt(n / 10);
}
document.write(pos);
}
var N = 777;
findPosition(N);
</script>
|
Time Complexity: O(log10N * log2N), where N represents the given integer.
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Share your thoughts in the comments
Please Login to comment...