Find if two given Quadratic equations have common roots or not

Given values a1, b1 and c1 of first Quadratic equations 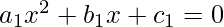and values a2, b2 and c2 of second Quadratic equations 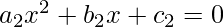, the task is to find whether both quadratic equations have common roots or not.
Examples:

Input: a1 = 1, b1 = -5, c1 = 6, a2 = 2, b2 = -10, c2 = 12 
Output: Yes 
Explanation:
Roots of both quadratic equations are (2, 3)
Input: a1 = 1, b1 = -5, c1 = 6, a2 = 1, b2 = -9, c2 = 20 
Output: No 
Explanation:
Roots of first quadratic equations are (2, 3), and Roots of second quadratic equations are (4, 5) 
Therefore, both quadratic equations have different roots. 

Approach:
Let the two quadratic equations are 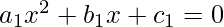and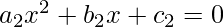 

• Let us assume the given condition to be true, i.e. both the equations have common roots, say 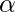and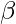 
  
• As we know that 
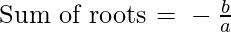  and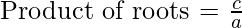 
  where a, b, c represents the quadratic equation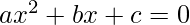 
  
• Therefore, 
  For 1st quadratic equation: 
  
  
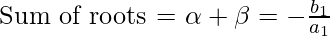
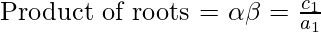
  Similarly, for 2nd quadratic equation: 
  
  
  
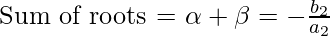
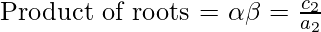
• Now since both the roots are common, 
  Therefore, from above equations 
  
  
  
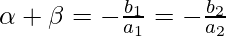
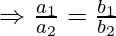
• Also, 
  
  
  
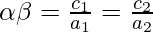
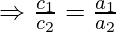
• Combining the above equations:

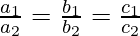
• which is the required condition for both roots to be common of the two quadratic equations.

Programs:

C++

// C++ Program to Find if two given
// Quadratic equations have
// common roots or not

#include <iostream>
using namespace std;

// function to check if 2 quadratic
// equations have common roots or not.
bool checkSolution(float a1, float b1,
                   float c1, float a2,
                   float b2, float c2)
{
    return (a1 / a2) == (b1 / b2)
           && (b1 / b2) == (c1 / c2);
}

// Driver code
int main()
{
    float a1 = 1, b1 = -5, c1 = 6;
    float a2 = 2, b2 = -10, c2 = 12;
    if (checkSolution(a1, b1, c1, a2, b2, c2))
        cout << "Yes";
    else
        cout << "No";
    return 0;
}

Java

// Java Program to Find if two given
// quadratic equations have common
// roots or not
class GFG {

// Function to check if 2 quadratic
// equations have common roots or not.
static boolean checkSolution(float a1, float b1,
                             float c1, float a2,
                             float b2, float c2)
{
    return ((a1 / a2) == (b1 / b2) &&
            (b1 / b2) == (c1 / c2));
}

// Driver code
public static void main (String[] args)
{
    float a1 = 1, b1 = -5, c1 = 6;
    float a2 = 2, b2 = -10, c2 = 12;

    if (checkSolution(a1, b1, c1, a2, b2, c2))
        System.out.println("Yes");
    else
        System.out.println("No");
}
}

// This code is contributed by AnkitRai01

Python3

# Python3 program to find if two given
# quadratic equations have common
# roots or not

# Function to check if 2 quadratic
# equations have common roots or not.
def checkSolution(a1, b1, c1, a2, b2, c2):

    return ((a1 / a2) == (b1 / b2) and
            (b1 / b2) == (c1 / c2))

# Driver code
a1, b1, c1 = 1, -5, 6
a2, b2, c2 = 2, -10, 12

if (checkSolution(a1, b1, c1, a2, b2, c2)):
    print("Yes")
else:
    print("No")

# This code is contributed by divyamohan123

C#

// C# Program to Find if two given
// quadratic equations have common
// roots or not
using System;
class GFG{

// Function to check if 2 quadratic
// equations have common roots or not.
static bool checkSolution(float a1, float b1,
                          float c1, float a2,
                          float b2, float c2)
{
    return ((a1 / a2) == (b1 / b2) &&
            (b1 / b2) == (c1 / c2));
}

// Driver code
public static void Main (string[] args)
{
    float a1 = 1, b1 = -5, c1 = 6;
    float a2 = 2, b2 = -10, c2 = 12;

    if (checkSolution(a1, b1, c1, a2, b2, c2))
        Console.WriteLine("Yes");
    else
        Console.WriteLine("No");
}
}

// This code is contributed by AnkitRai01

Javascript

<script>

// Javascript Program to Find if two given
// Quadratic equations have
// common roots or not

// function to check if 2 quadratic
// equations have common roots or not.
function checkSolution(a1, b1, c1, a2, b2, c2)
{
    return (a1 / a2) == (b1 / b2)
           && (b1 / b2) == (c1 / c2);
}

// Driver code
a1 = 1, b1 = -5, c1 = 6;
a2 = 2, b2 = -10, c2 = 12;
if (checkSolution(a1, b1, c1, a2, b2, c2))
    document.write("Yes");
else
    document.write("No");

</script>

Output:

Yes

Time Complexity: O(1)

Auxiliary Space: O(1)