Euler’s Totient function Φ(n) for an input n is the count of numbers in {1, 2, 3, …, n-1} that are relatively prime to n, i.e., the numbers whose GCD (Greatest Common Divisor) with n is 1.
Examples :
Φ(1) = 1
gcd(1, 1) is 1
Φ(2) = 1
gcd(1, 2) is 1, but gcd(2, 2) is 2.
Φ(3) = 2
gcd(1, 3) is 1 and gcd(2, 3) is 1
Φ(4) = 2
gcd(1, 4) is 1 and gcd(3, 4) is 1
Φ(5) = 4
gcd(1, 5) is 1, gcd(2, 5) is 1,
gcd(3, 5) is 1 and gcd(4, 5) is 1
Φ(6) = 2
gcd(1, 6) is 1 and gcd(5, 6) is 1,
How to compute Φ(n) for an input n?
A simple solution is to iterate through all numbers from 1 to n-1 and count numbers with gcd with n as 1. Below is the implementation of the simple method to compute Euler’s Totient function for an input integer n.
C
// A simple C program to calculate Euler's Totient Function
#include <stdio.h>
// Function to return gcd of a and b
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate Euler Totient Function
int phi(unsigned int n)
{
unsigned int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
printf("phi(%d) = %d\n", n, phi(n));
return 0;
}
// A simple java program to calculate
// Euler's Totient Function
import java.io.*;
class GFG {
// Function to return GCD of a and b
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate
// Euler Totient Function
static int phi(int n)
{
int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver code
public static void main(String[] args)
{
int n;
for (n = 1; n <= 10; n++)
System.out.println("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by sunnusingh
# A simple Python3 program
# to calculate Euler's
# Totient Function
# Function to return
# gcd of a and b
def gcd(a, b):
if (a == 0):
return b
return gcd(b % a, a)
# A simple method to evaluate
# Euler Totient Function
def phi(n):
result = 1
for i in range(2, n):
if (gcd(i, n) == 1):
result+=1
return result
# Driver Code
for n in range(1, 11):
print("phi(",n,") = ",
phi(n), sep = "")
# This code is contributed
# by Smitha
// A simple C# program to calculate
// Euler's Totient Function
using System;
class GFG {
// Function to return GCD of a and b
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate
// Euler Totient Function
static int phi(int n)
{
int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver code
public static void Main()
{
for (int n = 1; n <= 10; n++)
Console.WriteLine("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by nitin mittal
<script>
// Javascript program to calculate
// Euler's Totient Function
// Function to return
// gcd of a and b
function gcd(a, b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate
// Euler Totient Function
function phi(n)
{
let result = 1;
for (let i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver Code
for (let n = 1; n <= 10; n++)
document.write(`phi(${n}) = ${phi(n)} <br>`);
// This code is contributed by _saurabh_jaiswal
</script>
<Φphp
// PHP program to calculate
// Euler's Totient Function
// Function to return
// gcd of a and b
function gcd($a, $b)
{
if ($a == 0)
return $b;
return gcd($b % $a, $a);
}
// A simple method to evaluate
// Euler Totient Function
function phi($n)
{
$result = 1;
for ($i = 2; $i < $n; $i++)
if (gcd($i, $n) == 1)
$result++;
return $result;
}
// Driver Code
for ($n = 1; $n <= 10; $n++)
echo "phi(" .$n. ") =" . phi($n)."\n";
// This code is contributed by Sam007
Φ>
// A simple C++ program to calculate
// Euler's Totient Function
#include <iostream>
using namespace std;
// Function to return gcd of a and b
int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
// A simple method to evaluate Euler Totient Function
int phi(unsigned int n)
{
unsigned int result = 1;
for (int i = 2; i < n; i++)
if (gcd(i, n) == 1)
result++;
return result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
cout << "phi("<<n<<") = " << phi(n) << endl;
return 0;
}
// This code is contributed by SHUBHAMSINGH10
Outputphi(1) = 1
phi(2) = 1
phi(3) = 2
phi(4) = 2
phi(5) = 4
phi(6) = 2
phi(7) = 6
phi(8) = 4
phi(9) = 6
phi(10) = 4
The above code calls gcd function O(n) times. The time complexity of the gcd function is O(h) where “h” is the number of digits in a smaller number of given two numbers. Therefore, an upper bound on the time complexity of the above solution is O(N^2 log N) [How Φ there can be at most Log10n digits in all numbers from 1 to n]
Auxiliary Space: O(log N)
Below is a Better Solution. The idea is based on Euler’s product formula which states that the value of totient functions is below the product overall prime factors p of n.
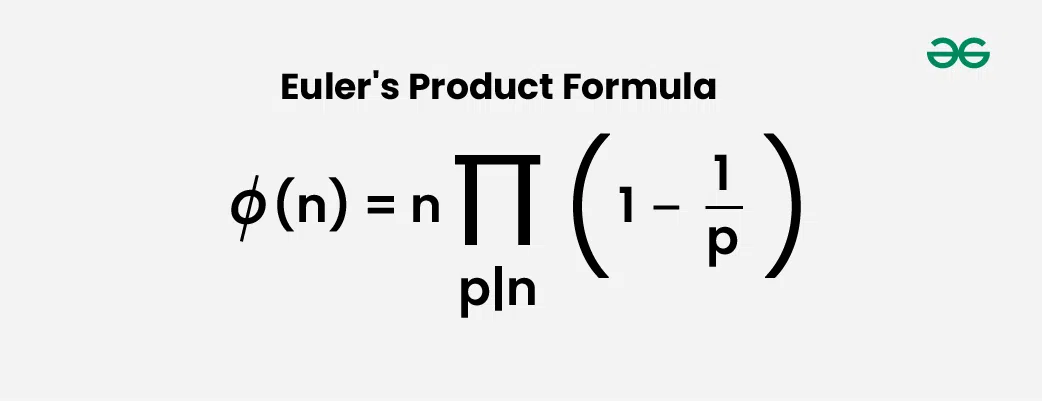
The formula basically says that the value of Φ(n) is equal to n multiplied by-product of (1 – 1/p) for all prime factors p of n. For example value of Φ(6) = 6 * (1-1/2) * (1 – 1/3) = 2.
We can find all prime factors using the idea used in this post.
1) Initialize : result = n
2) Run a loop from 'p' = 2 to sqrt(n), do following for every 'p'.
a) If p divides n, then
Set: result = result * (1.0 - (1.0 / (float) p));
Divide all occurrences of p in n.
3) Return result
Below is the implementation of Euler’s product formula.
C++
// C++ program to calculate Euler's
// Totient Function using Euler's
// product formula
#include <bits/stdc++.h>
using namespace std;
int phi(int n)
{
// Initialize result as n
float result = n;
// Consider all prime factors of n
// and for every prime factor p,
// multiply result with (1 - 1/p)
for(int p = 2; p * p <= n; ++p)
{
// Check if p is a prime factor.
if (n % p == 0)
{
// If yes, then update n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return (int)result;
}
// Driver code
int main()
{
int n;
for(n = 1; n <= 10; n++)
{
cout << "Phi" << "("
<< n << ")" << " = "
<< phi(n) <<endl;
}
return 0;
}
// This code is contributed by koulick_sadhu
// C program to calculate Euler's Totient Function
// using Euler's product formula
#include <stdio.h>
int phi(int n)
{
float result = n; // Initialize result as n
// Consider all prime factors of n and for every prime
// factor p, multiply result with (1 - 1/p)
for (int p = 2; p * p <= n; ++p) {
// Check if p is a prime factor.
if (n % p == 0) {
// If yes, then update n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return (int)result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
printf("phi(%d) = %d\n", n, phi(n));
return 0;
}
// Java program to calculate Euler's Totient
// Function using Euler's product formula
import java.io.*;
class GFG {
static int phi(int n)
{
// Initialize result as n
float result = n;
// Consider all prime factors of n and for
// every prime factor p, multiply result
// with (1 - 1/p)
for (int p = 2; p * p <= n; ++p) {
// Check if p is a prime factor.
if (n % p == 0) {
// If yes, then update n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return (int)result;
}
// Driver program to test above function
public static void main(String args[])
{
int n;
for (n = 1; n <= 10; n++)
System.out.println("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by Nikita Tiwari.
# Python 3 program to calculate
# Euler's Totient Function
# using Euler's product formula
def phi(n) :
result = n # Initialize result as n
# Consider all prime factors
# of n and for every prime
# factor p, multiply result with (1 - 1 / p)
p = 2
while p * p<= n :
# Check if p is a prime factor.
if n % p == 0 :
# If yes, then update n and result
while n % p == 0 :
n = n // p
result = result * (1.0 - (1.0 / float(p)))
p = p + 1
# If n has a prime factor
# greater than sqrt(n)
# (There can be at-most one
# such prime factor)
if n > 1 :
result -= result // n
#Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
#if n is a prime number
return int(result)
# Driver program to test above function
for n in range(1, 11) :
print("phi(", n, ") = ", phi(n))
# This code is contributed
# by Nikita Tiwari.
// C# program to calculate Euler's Totient
// Function using Euler's product formula
using System;
class GFG {
static int phi(int n)
{
// Initialize result as n
float result = n;
// Consider all prime factors
// of n and for every prime
// factor p, multiply result
// with (1 - 1 / p)
for (int p = 2; p * p <= n; ++p)
{
// Check if p is a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result *= (float)(1.0 - (1.0 / (float)p));
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return (int)result;
}
// Driver Code
public static void Main()
{
int n;
for (n = 1; n <= 10; n++)
Console.WriteLine("phi(" + n + ") = " + phi(n));
}
}
// This code is contributed by nitin mittal.
// Javascript program to calculate
// Euler's Totient Function
// using Euler's product formula
function phi(n)
{
// Initialize result as n
let result = n;
// Consider all prime factors
// of n and for every prime
// factor p, multiply result
// with (1 - 1/p)
for (let p = 2; p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result *= (1.0 - (1.0 / p));
}
}
// If n has a prime factor greater
// than sqrt(n) (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return parseInt(result);
}
// Driver Code
for (let n = 1; n <= 10; n++)
document.write(`phi(${n}) = ${phi(n)} <br>`);
// This code is contributed by _saurabh_jaiswal
<Φphp
// PHP program to calculate
// Euler's Totient Function
// using Euler's product formula
function phi($n)
{
// Initialize result as n
$result = $n;
// Consider all prime factors
// of n and for every prime
// factor p, multiply result
// with (1 - 1/p)
for ($p = 2; $p * $p <= $n; ++$p)
{
// Check if p is
// a prime factor.
if ($n % $p == 0)
{
// If yes, then update
// n and result
while ($n % $p == 0)
$n /= $p;
$result *= (1.0 - (1.0 / $p));
}
}
// If n has a prime factor greater
// than sqrt(n) (There can be at-most
// one such prime factor)
if ($n > 1)
$result -= $result / $n;
//Since in the set {1,2,....,n-1}, all numbers are relatively prime with n
//if n is a prime number
return intval($result);
}
// Driver Code
for ($n = 1; $n <= 10; $n++)
echo "phi(" .$n. ") =" . phi($n)."\n";
// This code is contributed by Sam007
Φ>
OutputPhi(1) = 1
Phi(2) = 1
Phi(3) = 2
Phi(4) = 2
Phi(5) = 4
Phi(6) = 2
Phi(7) = 6
Phi(8) = 4
Phi(9) = 6
Phi(10) = 4
Time Complexity: O(Φ n log n)
Auxiliary Space: O(1)
We can avoid floating-point calculations in the above method. The idea is to count all prime factors and their multiples and subtract this count from n to get the totient function value (Prime factors and multiples of prime factors won’t have gcd as 1)
1) Initialize result as n
2) Consider every number 'p' (where 'p' varies from 2 to Φ(n)).
If p divides n, then do following
a) Subtract all multiples of p from 1 to n [all multiples of p
will have gcd more than 1 (at least p) with n]
b) Update n by repeatedly dividing it by p.
3) If the reduced n is more than 1, then remove all multiples
of n from result.
Below is the implementation of the above algorithm.
C++
// C++ program to calculate Euler's
// Totient Function
#include <bits/stdc++.h>
using namespace std;
int phi(int n)
{
// Initialize result as n
int result = n;
// Consider all prime factors of n
// and subtract their multiples
// from result
for(int p = 2; p * p <= n; ++p)
{
// Check if p is a prime factor.
if (n % p == 0)
{
// If yes, then update n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver code
int main()
{
int n;
for(n = 1; n <= 10; n++)
{
cout << "Phi" << "("
<< n << ")" << " = "
<< phi(n) << endl;
}
return 0;
}
// This code is contributed by koulick_sadhu
// C program to calculate Euler's Totient Function
#include <stdio.h>
int phi(int n)
{
int result = n; // Initialize result as n
// Consider all prime factors of n and subtract their
// multiples from result
for (int p = 2; p * p <= n; ++p) {
// Check if p is a prime factor.
if (n % p == 0) {
// If yes, then update n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor greater than sqrt(n)
// (There can be at-most one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver program to test above function
int main()
{
int n;
for (n = 1; n <= 10; n++)
printf("phi(%d) = %d\n", n, phi(n));
return 0;
}
// Java program to calculate
// Euler's Totient Function
import java.io.*;
class GFG
{
static int phi(int n)
{
// Initialize result as n
int result = n;
// Consider all prime factors
// of n and subtract their
// multiples from result
for (int p = 2; p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver Code
public static void main (String[] args)
{
int n;
for (n = 1; n <= 10; n++)
System.out.println("phi(" + n +
") = " + phi(n));
}
}
// This code is contributed by ajit
# Python3 program to calculate
# Euler's Totient Function
def phi(n):
# Initialize result as n
result = n;
# Consider all prime factors
# of n and subtract their
# multiples from result
p = 2;
while(p * p <= n):
# Check if p is a
# prime factor.
if (n % p == 0):
# If yes, then
# update n and result
while (n % p == 0):
n = int(n / p);
result -= int(result / p);
p += 1;
# If n has a prime factor
# greater than sqrt(n)
# (There can be at-most
# one such prime factor)
if (n > 1):
result -= int(result / n);
return result;
# Driver Code
for n in range(1, 11):
print("phi(",n,") =", phi(n));
# This code is contributed
# by mits
// C# program to calculate
// Euler's Totient Function
using System;
class GFG
{
static int phi(int n)
{
// Initialize result as n
int result = n;
// Consider all prime
// factors of n and
// subtract their
// multiples from result
for (int p = 2;
p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then update
// n and result
while (n % p == 0)
n /= p;
result -= result / p;
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= result / n;
return result;
}
// Driver Code
static public void Main ()
{
int n;
for (n = 1; n <= 10; n++)
Console.WriteLine("phi(" + n +
") = " +
phi(n));
}
}
// This code is contributed
// by akt_mit
// Javascript program to calculate
// Euler's Totient Function
function phi(n)
{
// Initialize
// result as n
let result = n;
// Consider all prime
// factors of n and subtract
// their multiples from result
for (let p = 2;
p * p <= n; ++p)
{
// Check if p is
// a prime factor.
if (n % p == 0)
{
// If yes, then
// update n and result
while (n % p == 0)
n = parseInt(n / p);
result -= parseInt(result / p);
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if (n > 1)
result -= parseInt(result / n);
return result;
}
// Driver Code
for (let n = 1; n <= 10; n++)
document.write(`phi(${n}) = ${phi(n)} <br>`);
// This code is contributed
// by _saurabh_jaiswal
<Φphp
// PHP program to calculate
// Euler's Totient Function
function phi($n)
{
// Initialize
// result as n
$result = $n;
// Consider all prime
// factors of n and subtract
// their multiples from result
for ($p = 2;
$p * $p <= $n; ++$p)
{
// Check if p is
// a prime factor.
if ($n % $p == 0)
{
// If yes, then
// update n and result
while ($n % $p == 0)
$n = (int)$n / $p;
$result -= (int)$result / $p;
}
}
// If n has a prime factor
// greater than sqrt(n)
// (There can be at-most
// one such prime factor)
if ($n > 1)
$result -= (int)$result / $n;
return $result;
}
// Driver Code
for ($n = 1; $n <= 10; $n++)
echo "phi(", $n,") =",
phi($n), "\n";
// This code is contributed
// by ajit
Φ>
OutputPhi(1) = 1
Phi(2) = 1
Phi(3) = 2
Phi(4) = 2
Phi(5) = 4
Phi(6) = 2
Phi(7) = 6
Phi(8) = 4
Phi(9) = 6
Phi(10) = 4
Time Complexity: O(Φ n log n)
Auxiliary Space: O(1)
Let us take an example to understand the above algorithm.
n = 10.
Initialize: result = 10
2 is a prime factor, so n = n/i = 5, result = 5
3 is not a prime factor.
The for loop stops after 3 as 4*4 is not less than or equal
to 10.
After for loop, result = 5, n = 5
Since n > 1, result = result - result/n = 4
Some Interesting Properties of Euler’s Totient Function
1) For a prime number p, 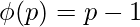
Proof :
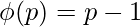 , where p is any prime numberWe know that
, where p is any prime numberWe know that 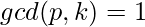 where k is any random number and
where k is any random number and 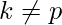 [Tex]\\[/Tex]Total number from 1 to p = p Number for which
[Tex]\\[/Tex]Total number from 1 to p = p Number for which 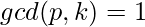 is
is 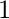 , i.e the number p itself, so subtracting 1 from p
, i.e the number p itself, so subtracting 1 from p 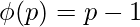
Examples :
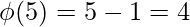 [Tex]\\[/Tex]
[Tex]\\[/Tex]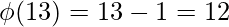 [Tex]\\[/Tex]
[Tex]\\[/Tex]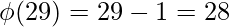
2) For two prime numbers a and b , used in RSA Algorithm
, used in RSA Algorithm
Proof :
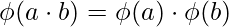 , where a and b are prime numbers
, where a and b are prime numbers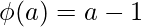 ,
, 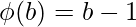 [Tex]\\[/Tex]Total number from 1 to ab = ab Total multiples of a from 1 to ab =
[Tex]\\[/Tex]Total number from 1 to ab = ab Total multiples of a from 1 to ab = 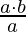 =
= 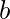 Total multiples of b from 1 to ab =
Total multiples of b from 1 to ab = 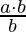 =
= 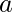 Example:a = 5, b = 7, ab = 35Multiples of a =
Example:a = 5, b = 7, ab = 35Multiples of a = 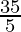 = 7 {5, 10, 15, 20, 25, 30, 35}Multiples of b =
= 7 {5, 10, 15, 20, 25, 30, 35}Multiples of b = 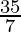 = 5 {7, 14, 21, 28, 35}
= 5 {7, 14, 21, 28, 35} Can there be any double counting ?(watch above example carefully, try with other prime numbers also for more grasp)Ofcourse, we have counted
Can there be any double counting ?(watch above example carefully, try with other prime numbers also for more grasp)Ofcourse, we have counted 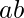 twice in multiples of a and multiples of b so, Total multiples = a + b - 1 (with which
twice in multiples of a and multiples of b so, Total multiples = a + b - 1 (with which 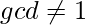 with
with 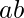 )
) [Tex]\phi(ab) = ab - (a + b - 1)[/Tex] , removing all number with
[Tex]\phi(ab) = ab - (a + b - 1)[/Tex] , removing all number with 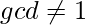 with
with 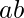
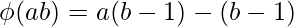 [Tex]\phi(ab) = (a - 1) \cdot (b - 1)[/Tex]
[Tex]\phi(ab) = (a - 1) \cdot (b - 1)[/Tex]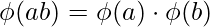
Examples :
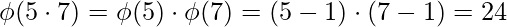 [Tex]\\[/Tex]
[Tex]\\[/Tex]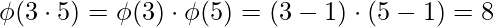 [Tex]\\[/Tex]
[Tex]\\[/Tex]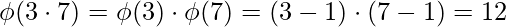
3) For a prime number p, 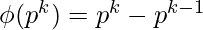
Proof :
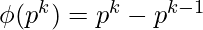 , where p is a prime number
, where p is a prime number Total numbers from 1 to
Total numbers from 1 to 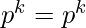 Total multiples of
Total multiples of 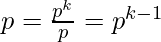 Removing these multiples as with them
Removing these multiples as with them 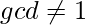 [Tex]\\[/Tex]Example : p = 2, k = 5,
[Tex]\\[/Tex]Example : p = 2, k = 5, 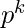 = 32Multiples of 2 (as with them
= 32Multiples of 2 (as with them 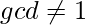 ) = 32 / 2 = 16 {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32}
) = 32 / 2 = 16 {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32} [Tex]\phi(p ^ k) = p ^ k - p ^ {k - 1}[/Tex]
[Tex]\phi(p ^ k) = p ^ k - p ^ {k - 1}[/Tex]
Examples :
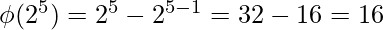 [Tex]\\[/Tex]
[Tex]\\[/Tex]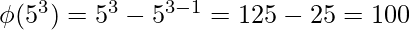 [Tex]\\[/Tex]
[Tex]\\[/Tex]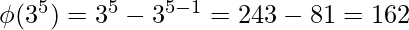
4) For two number a and b 

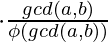
Special Case : gcd(a, b) = 1
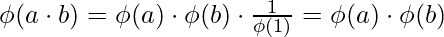
Examples :
Special Case : 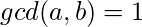 ,
, 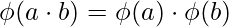
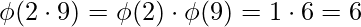 [Tex]\\[/Tex]
[Tex]\\[/Tex]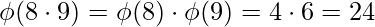 [Tex]\\[/Tex]
[Tex]\\[/Tex]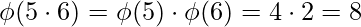
 [Tex]\\[/Tex]Normal Case :
[Tex]\\[/Tex]Normal Case : 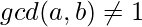 ,
, 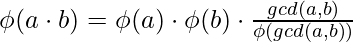 [Tex]\\[/Tex]
[Tex]\\[/Tex]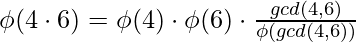
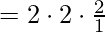
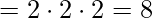 [Tex]\\[/Tex]
[Tex]\\[/Tex]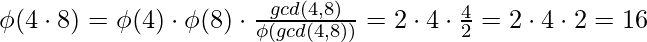 [Tex]\\[/Tex]
[Tex]\\[/Tex]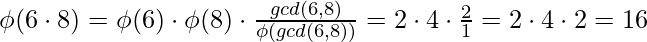
5) Sum of values of totient functions of all divisors of n is equal to n.

Examples :
n = 6
factors = {1, 2, 3, 6}
n = 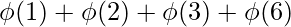 = 1 + 1 + 2 + 2 = 6
= 1 + 1 + 2 + 2 = 6 n = 8factors = {1, 2, 4, 8}n =
n = 8factors = {1, 2, 4, 8}n = 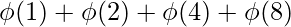 = 1 + 1 + 2 + 4 = 8
= 1 + 1 + 2 + 4 = 8 n = 10factors = {1, 2, 5, 10}n =
n = 10factors = {1, 2, 5, 10}n = 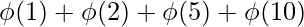 = 1 + 1 + 4 + 4 = 10
= 1 + 1 + 4 + 4 = 10
6) The most famous and important feature is expressed in Euler’s theorem :
The theorem states that if n and a are coprime
(or relatively prime) positive integers, then
aΦ(n) Φ 1 (mod n)
The RSA cryptosystem is based on this theorem:
In the particular case when m is prime say p, Euler’s theorem turns into the so-called Fermat’s little theorem :
ap-1 Φ 1 (mod p)
7) Number of generators of a finite cyclic group under modulo n addition is Φ(n).
Related Article:
Euler’s Totient function for all numbers smaller than or equal to n
Optimized Euler Totient Function for Multiple Evaluations
References:
http://e-maxx.ru/algo/euler_function
http://en.wikipedia.org/wiki/Euler%27s_totient_function
https://cp-algorithms.com/algebra/phi-function.html
http://mathcenter.oxford.memory.edu/site/math125/chineseRemainderTheorem/
Share your thoughts in the comments
Please Login to comment...