Probability of Euler’s Totient Function in a range [L, R] to be divisible by M
Last Updated :
25 May, 2021
Given three integers L, R, and M, the task is to find the probability of Euler’s Totient Function of a number in the range [L, R] is divisible by M.
Euler’s Totient function is the count of numbers in {1, 2, 3, …, N} that are relatively prime to N, i.e., the numbers whose GCD (Greatest Common Divisor) with N is 1.
Examples:
Input: L = 1, R = 5, M = 2
Output: 0.6
Explanation:
Euler’s Totient Function for N = 1, 2, 3, 4 and 5 is {1, 1, 2, 2, 4} respectively.
Count of Euler’s Totient Function divisible by M(= 2) is 3.
Therefore, the required probability is 3/5 = 0.6
Input: L = 1, R = 7, M = 4
Output: 0.142
Explanation:
Euler’s Totient Function for N = 1, 2, 3, ….7 is {1, 1, 2, 2, 4, 2, 6} respectively.
Count of Euler’s Totient Function divisible by M(= 4) is 1.
Therefore, the required probability is 1/7 = 0.142
Approach: The idea is to pre-compute Euler’s Totient Function and iterate over the given range and count the numbers divisible by M to calculate the probability.
For the computation of the Euler’s Totient Function, use the Euler’s Product Formula :
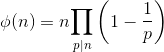
where pi is the prime factor of N.
For every prime factor i of N ( L <= n <= R), perform the following steps:
- Subtract all multiples of i from [1, N].
- Update N by repeatedly dividing it by i.
- If the reduced N is more than 1, then remove all multiples of N from result.
For the computation of the prime factors, use Sieve of Eratosthenes method. The probability in the given range will be count/(L – R + 1).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define size 1000001
void seiveOfEratosthenes(int* prime)
{
prime[0] = 1, prime[1] = 0;
for (int i = 2; i * i < 1000001; i++) {
if (prime[i] == 0) {
for (int j = i * i; j < 1000001;
j += i) {
prime[j] = 1;
}
}
}
}
float probabiltyEuler(int* prime, int L,
int R, int M)
{
int* arr = new int[size]{ 0 };
int* eulerTotient = new int[size]{ 0 };
int count = 0;
for (int i = L; i <= R; i++) {
eulerTotient[i - L] = i;
arr[i - L] = i;
}
for (int i = 2; i < 1000001; i++) {
if (prime[i] == 0) {
for (int j = (L / i) * i; j <= R;
j += i) {
if (j - L >= 0) {
eulerTotient[j - L]
= eulerTotient[j - L]
/ i * (i - 1);
while (arr[j - L] % i == 0) {
arr[j - L] /= i;
}
}
}
}
}
for (int i = L; i <= R; i++) {
if (arr[i - L] > 1) {
eulerTotient[i - L]
= (eulerTotient[i - L] / arr[i - L])
* (arr[i - L] - 1);
}
}
for (int i = L; i <= R; i++) {
if ((eulerTotient[i - L] % M) == 0) {
count++;
}
}
return (1.0 * count / (R + 1 - L));
}
int main()
{
int* prime = new int[size]{ 0 };
seiveOfEratosthenes(prime);
int L = 1, R = 7, M = 3;
cout << probabiltyEuler(prime, L, R, M);
return 0;
}
|
Java
import java.util.*;
class GFG{
static final int size = 1000001;
static void seiveOfEratosthenes(int []prime)
{
prime[0] = 1;
prime[1] = 0;
for (int i = 2; i * i < 1000001; i++)
{
if (prime[i] == 0)
{
for (int j = i * i; j < 1000001; j += i)
{
prime[j] = 1;
}
}
}
}
static float probabiltyEuler(int []prime, int L,
int R, int M)
{
int[] arr = new int[size];
int []eulerTotient = new int[size];
int count = 0;
for (int i = L; i <= R; i++)
{
eulerTotient[i - L] = i;
arr[i - L] = i;
}
for (int i = 2; i < 1000001; i++)
{
if (prime[i] == 0)
{
for (int j = (L / i) * i; j <= R; j += i)
{
if (j - L >= 0)
{
eulerTotient[j - L] = eulerTotient[j - L] /
i * (i - 1);
while (arr[j - L] % i == 0)
{
arr[j - L] /= i;
}
}
}
}
}
for (int i = L; i <= R; i++)
{
if (arr[i - L] > 1)
{
eulerTotient[i - L] = (eulerTotient[i - L] / arr[i - L]) *
(arr[i - L] - 1);
}
}
for (int i = L; i <= R; i++)
{
if ((eulerTotient[i - L] % M) == 0)
{
count++;
}
}
return (float) (1.0 * count / (R + 1 - L));
}
public static void main(String[] args)
{
int []prime = new int[size];
seiveOfEratosthenes(prime);
int L = 1, R = 7, M = 3;
System.out.print(probabiltyEuler(prime, L, R, M));
}
}
|
Python3
size = 1000001
def seiveOfEratosthenes(prime):
prime[0] = 1
prime[1] = 0
i = 2
while(i * i < 1000001):
if (prime[i] == 0):
j = i * i
while(j < 1000001):
prime[j] = 1
j = j + i
i += 1
def probabiltyEuler(prime, L, R, M):
arr = [0] * size
eulerTotient = [0] * size
count = 0
for i in range(L, R + 1):
eulerTotient[i - L] = i
arr[i - L] = i
for i in range(2, 1000001):
if (prime[i] == 0):
for j in range((L // i) * i, R + 1, i):
if (j - L >= 0):
eulerTotient[j - L] = (eulerTotient[j - L] //
i * (i - 1))
while (arr[j - L] % i == 0):
arr[j - L] = arr[j - L] // i
for i in range(L, R + 1):
if (arr[i - L] > 1):
eulerTotient[i - L] = ((eulerTotient[i - L] //
arr[i - L]) *
(arr[i - L] - 1))
for i in range(L, R + 1):
if ((eulerTotient[i - L] % M) == 0):
count += 1
return (float)(1.0 * count / (R + 1 - L))
prime = [0] * size
seiveOfEratosthenes(prime)
L, R, M = 1, 7, 3
print(probabiltyEuler(prime, L, R, M))
|
C#
using System;
class GFG{
static readonly int size = 1000001;
static void seiveOfEratosthenes(int []prime)
{
prime[0] = 1;
prime[1] = 0;
for (int i = 2; i * i < 1000001; i++)
{
if (prime[i] == 0)
{
for (int j = i * i; j < 1000001; j += i)
{
prime[j] = 1;
}
}
}
}
static float probabiltyEuler(int []prime, int L,
int R, int M)
{
int[] arr = new int[size];
int []eulerTotient = new int[size];
int count = 0;
for (int i = L; i <= R; i++)
{
eulerTotient[i - L] = i;
arr[i - L] = i;
}
for (int i = 2; i < 1000001; i++)
{
if (prime[i] == 0)
{
for (int j = (L / i) * i; j <= R; j += i)
{
if (j - L >= 0)
{
eulerTotient[j - L] = eulerTotient[j - L] /
i * (i - 1);
while (arr[j - L] % i == 0)
{
arr[j - L] /= i;
}
}
}
}
}
for (int i = L; i <= R; i++)
{
if (arr[i - L] > 1)
{
eulerTotient[i - L] = (eulerTotient[i - L] / arr[i - L]) *
(arr[i - L] - 1);
}
}
for (int i = L; i <= R; i++)
{
if ((eulerTotient[i - L] % M) == 0)
{
count++;
}
}
return (float) (1.0 * count / (R + 1 - L));
}
public static void Main(String[] args)
{
int []prime = new int[size];
seiveOfEratosthenes(prime);
int L = 1, R = 7, M = 3;
Console.Write(probabiltyEuler(prime, L, R, M));
}
}
|
Javascript
<script>
let size = 1000001;
let prime = new Array(size,0);
function seiveOfEratosthenes()
{
prime[0] = 1;
prime[1] = 0;
for (let i = 2; i * i < 1000001; i++)
{
if (prime[i] == 0)
{
for (let j = i * i; j < 1000001; j += i)
{
prime[j] = 1;
}
}
}
}
function probabiltyEuler(L,R, M)
{
let arr = new Array(size,0);
let eulerTotient = new Array(size,0);
let count = 0;
for (let i = L; i <= R; i++)
{
eulerTotient[i - L] = i;
arr[i - L] = i;
}
for (let i = 2; i < 1000001; i++)
{
if (prime[i] == 0)
{
for (let j = (L / i) * i; j <= R; j += i)
{
if (j - L >= 0)
{
eulerTotient[j - L] =
eulerTotient[j - L] / i * (i - 1);
while (arr[j - L] % i == 0)
{
arr[j - L] /= i;
}
}
}
}
}
for (let i = L; i <= R; i++)
{
if (arr[i - L] > 1)
{
eulerTotient[i - L] =
(eulerTotient[i - L] / arr[i - L]) *
(arr[i - L] - 1);
}
}
for (let i = L; i <= R; i++)
{
if ((eulerTotient[i - L] % M) == 0)
{
count++;
}
}
count/=2;
return 1.0 * count / (R + 1 - L);
}
seiveOfEratosthenes();
let L = 1;
let R = 7;
let M = 3;
document.write(probabiltyEuler(L, R, M).toFixed(7));
</script>
|
Time Complexity : O(Nlog(N))
Auxiliary Space: O(size), where size denotes the number upto which Sieve is calculated.
Share your thoughts in the comments
Please Login to comment...