Euler Totient Function in Python

Euler’s Totient function, also known as Euler’s Phi Function Φ (n) is a mathematical function that counts the number of positive integers up to a given integer n that are relatively prime to n. i.e., the numbers whose GCD (Greatest Common Divisor) with n is 1.

Examples :

Input: Φ(1) = 1
Output: gcd(1, 1) is 1

Input: Φ(2) = 1
Output: gcd(1, 2) is 1, but gcd(2, 2) is 2.

Input: Φ(3) = 2
Output: gcd(1, 3) is 1 and gcd(2, 3) is 1

Using Iteration:

In this approach, we iterate through all numbers from 1 to n-1 and check if each number is coprime with n using the gcd function and find if the gcd of i and n is 1 thus incrementing the count of coprime numbers and finally returning the count.

Step-by-step approach:

• Define a GCD function to find the greatest common divisor.
• Define Euler’s Totient Function.
• Iterate through numbers from 1 to n-1.
• Check coprimality with n.
• Count coprime numbers.
• Return the count.
• Execute for numbers 1 to 10 and print the results.

Below is the implementation of the above approach:

Python3

# Python3 program  to calculate Euler's  Totient Function
 
# Function to return
# gcd of a and b
def gcd(a, b):
 
    if (a == 0):
        return b
    return gcd(b % a, a)
 

def euler_totient(n):
    # Initialize the count of coprime numbers to 0
    count = 0
    # Iterate from 1 to n-1
    for i in range(1, n):
        # Check if i and n are coprime using gcd
        if gcd(i, n) == 1:
            count += 1
    return count

# Driver program  
for n in range(1, 11) :
    print("Euler's Totient for", n, ":" , euler_totient(n))
  

Output

Euler's Totient for 1 : 0
Euler's Totient for 2 : 1
Euler's Totient for 3 : 2
Euler's Totient for 4 : 2
Euler's Totient for 5 : 4
Euler's Totient for 6 : 2
Euler's Totient for 7 : 6
Euler's Totient fo...

Time complexity: O(N^2 log N)
Auxiliary Space: O(log N)

Using Euler’s Product Formula:

The approach here is to use Euler’s Product Formula which states that the value of totient functions is below the product overall prime factors p of n to calculate Euler’s Totient Function.

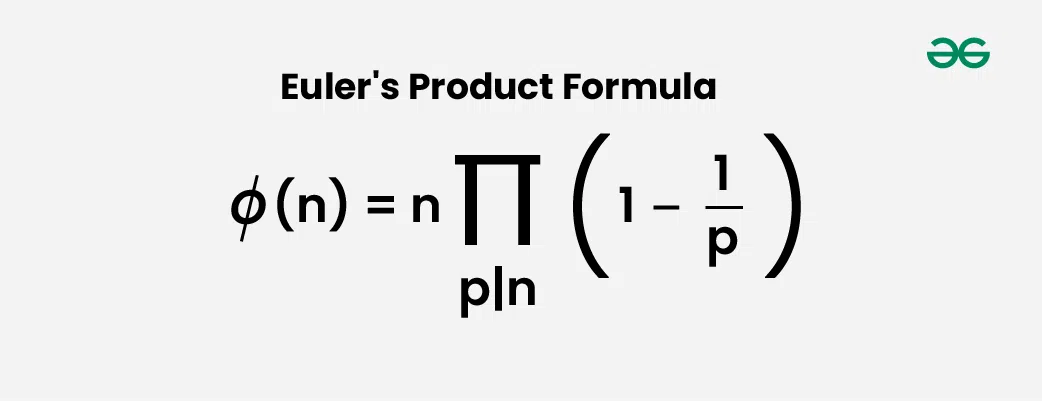
The formula basically says that the value of Φ(n) is equal to n multiplied by-product of (1 – 1/p) for all prime factors p of n. For example value of Φ(6) = 6 * (1-1/2) * (1 – 1/3) = 2.

Step by step approach:

• Initialize : result = n
• Run a loop from ‘p’ = 2 to sqrt(n), do following for every ‘p’.
  • If p divides n, then
    • Set: result = result * (1.0 – (1.0 / (float) p));
    • Divide all occurrences of p in n.
• Return result

Below is the implementation of the above approach:

Python3

# Python 3 program to calculate Euler's Totient Function using Euler's product formula
 
def euler_totient_product(n) :
 
    result = n   # Initialize result as n
      
  # Iterate through all prime factors of n
    p = 2
    while p * p<= n :
 
        # Check if p is a prime factor.
        if n % p == 0 :
 
            # If yes, then update n and result
            while n % p == 0 :
                n = n // p
            result = result * (1.0 - (1.0 / float(p)))
        p = p + 1
         
   # If n is prime
    if n > 1 :
        result -= result // n
    return int(result)
     
     
# Driver program  
for n in range(1, 11) :
    print("Euler's Totient for", n, ":", euler_totient_product(n))

Output

Euler's Totient for 1 : 1
Euler's Totient for 2 : 1
Euler's Totient for 3 : 2
Euler's Totient for 4 : 2
Euler's Totient for 5 : 4
Euler's Totient for 6 : 2
Euler's Totient for 7 : 6
Euler's Totient fo...

Time Complexity: O(√n log n),where n is the given integer
Auxiliary Space: O(1)