Euler’s Totient function for all numbers smaller than or equal to n

Euler’s Totient function ?(n) for an input n is the count of numbers in {1, 2, 3, …, n} that are relatively prime to n, i.e., the numbers whose GCD (Greatest Common Divisor) with n is 1.

For example, ?(4) = 2, ?(3) = 2 and ?(5) = 4. There are 2 numbers smaller or equal to 4 that are relatively prime to 4, 2 numbers smaller or equal to 3 that are relatively prime to 3. And 4 numbers smaller than or equal to 5 that are relatively prime to 5.
We have discussed different methods for the computation of ?(n) in the previous post. 

How to compute ? for all numbers smaller than or equal to n?

Example: 

Input: n = 5
Output: Totient of 1 is 1
        Totient of 2 is 1
        Totient of 3 is 2
        Totient of 4 is 2
        Totient of 5 is 4

We strongly recommend you to minimize your browser and try this yourself first.
A Simple Solution is to call ?(i) for i = 1 to n. 

An Efficient Solution is to use an idea similar to the Sieve of Eratosthenes to precompute all values. The method is based on below product formula.

The formula basically says that the value of ?(n) is equal to n multiplied by-product of (1 – 1/p) for all prime factors p of n. For example value of ?(6) = 6 * (1-1/2) * (1 – 1/3) = 2.

Below is the complete algorithm: 

1) Create an array phi[1..n] to store ? values of all numbers 
   from 1 to n.  

2) Initialize all values such that phi[i] stores i.  This
   initialization serves two purposes.
   a) To check if phi[i] is already evaluated or not. Note that
      the maximum possible phi value of a number i is i-1.
   b) To initialize phi[i] as i is multiple in the above product
      formula. 

3) Run a loop for p = 2 to n
    a) If phi[p] is p, means p is not evaluated yet and p is a 
       prime number (similar to Sieve), otherwise phi[p] must 
       have been updated in step 3.b
    b) Traverse through all multiples of p and update all 
       multiples of p by multiplying with (1-1/p).

4) Run a loop from i = 1 to n and print all Ph[i] values.

Below is the implementation of above algorithm. 

C++

// C++ program to compute Totient function for
// all numbers smaller than or equal to n.
#include<iostream>
using namespace std;

// Computes and prints totient of all numbers
// smaller than or equal to n.
void computeTotient(int n)
{
    // Create and initialize an array to store
    // phi or totient values
    long long phi[n+1];
    for (int i=1; i<=n; i++)
        phi[i] = i; // indicates not evaluated yet
                    // and initializes for product
                    // formula.

    // Compute other Phi values
    for (int p=2; p<=n; p++)
    {
        // If phi[p] is not computed already,
        // then number p is prime
        if (phi[p] == p)
        {
            // Phi of a prime number p is
            // always equal to p-1.
            phi[p] = p-1;

            // Update phi values of all
            // multiples of p
            for (int i = 2*p; i<=n; i += p)
            {
            // Add contribution of p to its
            // multiple i by multiplying with
            // (1 - 1/p)
            phi[i] = (phi[i]/p) * (p-1);
            }
        }
    }

    // Print precomputed phi values
    for (int i=1; i<=n; i++)
    cout << "Totient of " << i << " is "
        << phi[i] << endl;
}

// Driver program to test above function
int main()
{
    int n = 12;
    computeTotient(n);
    return 0;
}

Java

// Java program to compute Totient
// function for all numbers smaller
// than or equal to n.
import java.util.*;

class GFG {

// Computes and prints totient of all numbers
// smaller than or equal to n.
static void computeTotient(int n) {

    // Create and initialize an array to store
    // phi or totient values
    long phi[] = new long[n + 1];
    for (int i = 1; i <= n; i++)
    phi[i] = i; // indicates not evaluated yet
                // and initializes for product
                // formula.

    // Compute other Phi values
    for (int p = 2; p <= n; p++) {

    // If phi[p] is not computed already,
    // then number p is prime
    if (phi[p] == p) {

        // Phi of a prime number p is
        // always equal to p-1.
        phi[p] = p - 1;

        // Update phi values of all
        // multiples of p
        for (int i = 2 * p; i <= n; i += p) {

        // Add contribution of p to its
        // multiple i by multiplying with
        // (1 - 1/p)
        phi[i] = (phi[i] / p) * (p - 1);
        }
    }
    }

    // Print precomputed phi values
    for (int i = 1; i <= n; i++)
    System.out.println("Totient of " + i +
                        " is " + phi[i]);
}

// Driver code
public static void main(String[] args) {

    int n = 12;
    computeTotient(n);
}
}

// This code is contributed by Anant Agarwal.

Python3

# Python program to compute
# Totient function for
# all numbers smaller than
# or equal to n.

# Computes and prints
# totient of all numbers
# smaller than or equal to n.
def computeTotient(n):

    # Create and initialize
    # an array to store
    # phi or totient values
    phi=[]
    for i in range(n + 2):
        phi.append(0)

    for i in range(1, n+1):

        phi[i] = i # indicates not evaluated yet
                    # and initializes for product
                    # formula.

    # Compute other Phi values
    for p in range(2,n+1):

        # If phi[p] is not computed already,
        # then number p is prime
        if (phi[p] == p):

            # Phi of a prime number p is
            # always equal to p-1.
            phi[p] = p-1

            # Update phi values of all
            # multiples of p
            for i in range(2*p,n+1,p):

                # Add contribution of p to its
                # multiple i by multiplying with
                # (1 - 1/p)
                phi[i] = (phi[i]//p) * (p-1)


    # Print precomputed phi values
    for i in range(1,n+1):
        print("Totient of ", i ," is ",
        phi[i])

# Driver code

n = 12
computeTotient(n)

# This code is contributed
# by Anant Agarwal

C#

// C# program to check if given two
// strings are at distance one.
using System;

class GFG
{

// Computes and prints totient of all
// numbers smaller than or equal to n
static void computeTotient(int n)
{

    // Create and initialize an array to
    // store phi or totient values
    long []phi = new long[n + 1];
    for (int i = 1; i <= n; i++)

    // indicates not evaluated yet
    // and initializes for product
    // formula.
    phi[i] = i;

    // Compute other Phi values
    for (int p = 2; p <= n; p++)
    {

    // If phi[p] is not computed already,
    // then number p is prime
    if (phi[p] == p)
    {

        // Phi of a prime number p is
        // always equal to p-1.
        phi[p] = p - 1;

        // Update phi values of all
        // multiples of p
        for (int i = 2 * p; i <= n; i += p)
        {

        // Add contribution of p to its
        // multiple i by multiplying with
        // (1 - 1/p)
        phi[i] = (phi[i] / p) * (p - 1);

        }
    }
    }

    // Print precomputed phi values
    for (int i = 1; i <= n; i++)
    Console.WriteLine("Totient of " + i +" is " + phi[i]);
}

// Driver code
public static void Main()
{

    int n = 12;
    computeTotient(n);
}
}

// This code is contributed by Sam007.

PHP

<?php
// PHP program to compute Totient
// function for all numbers smaller
// than or equal to n.

// Computes and prints totient
// of all numbers smaller than
// or equal to n.
function computeTotient($n)
{

    // Create and initialize
    // an array to store
    // phi or totient values
    for($i = 1; $i <= $n; $i++)

        // indicates not evaluated yet
        // and initializes for product
        // formula.
        $phi[$i] = $i;

    // Compute other Phi values
    for($p = 2; $p <= $n; $p++)
    {

        // If phi[p] is not computed already,
        // then number p is prime
        if ($phi[$p] == $p)
        {

            // Phi of a prime number p is
            // always equal to p-1.
            $phi[$p] = $p - 1;

            // Update phi values of all
            // multiples of p
            for($i = 2 * $p; $i <= $n; $i += $p)
            {

                // Add contribution of p to its
                // multiple i by multiplying with
                // (1 - 1/$p)
                $phi[$i] = ($phi[$i] / $p) * ($p - 1);
            }
        }
    }

    // Print precomputed phi values
    for($i = 1; $i <= $n; $i++)
    echo "Totient of " , $i , " is ",
        $phi[$i] ,"\n";
}

    // Driver Code
    $n = 12;
    computeTotient($n);

// This code is contributed by ajit
?>

Javascript

<script>
    // Javascript program to check if given two
    // strings are at distance one.

    // Computes and prints totient of all
    // numbers smaller than or equal to n
    function computeTotient(n)
    {

        // Create and initialize an array to
        // store phi or totient values
        let phi = new Array(n + 1);
        for (let i = 1; i <= n; i++)

        // indicates not evaluated yet
        // and initializes for product
        // formula.
        phi[i] = i;

        // Compute other Phi values
        for (let p = 2; p <= n; p++)
        {

          // If phi[p] is not computed already,
          // then number p is prime
          if (phi[p] == p)
          {

              // Phi of a prime number p is
              // always equal to p-1.
              phi[p] = p - 1;

              // Update phi values of all
              // multiples of p
              for (let i = 2 * p; i <= n; i += p)
              {

              // Add contribution of p to its
              // multiple i by multiplying with
              // (1 - 1/p)
              phi[i] = parseInt(phi[i] / p, 10) * (p - 1);

              }
          }
        }

        // Print precomputed phi values
        for (let i = 1; i <= n; i++)
            document.write("Totient of " + i +" is " + phi[i] + "</br>");
    }

    let n = 12;
    computeTotient(n);
</script>

Output

Totient of 1 is 1
Totient of 2 is 1
Totient of 3 is 2
Totient of 4 is 2
Totient of 5 is 4
Totient of 6 is 2
Totient of 7 is 6
Totient of 8 is 4
Totient of 9 is 6
Totient of 10 is 4
Totient of 11 is 10
Totient of 12 is 4

Time Complexity: O(n²)

Auxiliary Space: O(n)

The same solution can be used when we have a large number of queries for computing the totient function. 

Another way to compute Euler’s totient function can also be done by using the below formula:

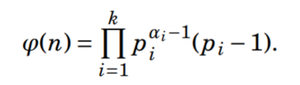
Euler’s totient function

Let us see an example to understand the above function, basically, it does the same job but in a different way:

For example, ?(12) = { (2^(2-1)) x (2-1) } x { (3^(1-1)) x (3-1) } =4

Note that ?(n) = n?1 if n is prime.

Below is the implementation of the above formula:

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
#define ll long long

ll Euler_totient_function(ll n)
{
    ll result = 1;
    for (ll i = 2; i * i <= n; i++) {
        ll c = 0;
        if (n % i == 0) {
            while (n % i == 0) {
                c++;
                n /= i;
            }
        }
        if (c > 0) {
            ll power = (ll)pow(i, c - 1);
            ll sm = (ll)pow(i, c - 1) * (i - 1);
            result *= sm;
        }
    }
    if (n > 1) {
        result *= (n - 1);
    }
    return result;
}

// driver code
int main()
{
    for (ll i = 1; i < 13; i++) {
        cout << "Euler_totient_function(" << i << "): ";
        cout << Euler_totient_function(i) << endl;
    }
}
#praveeny182

Java

// Java program for the above approach
import java.io.*;

class GFG{

static long Euler_totient_function(long n)
{
    long result = 1;
    for(long i = 2; i * i <= n; i++)
    {
        long c = 0;
        if (n % i == 0)
        {
            while (n % i == 0)
            {
                c++;
                n /= i;
            }
        }
        if (c > 0)
        {
            long power = (long)Math.pow(i, c - 1);
            long sm = (long)Math.pow(i, c - 1) * (i - 1);
            result *= sm;
        }
    }
    if (n > 1)
    {
        result *= (n - 1);
    }
    return result;
}

// Driver code
public static void main(String[] args)
{
    for(long i = 1; i < 13; i++)
    {
        System.out.print("Euler_totient_function(" +
                         i + "): ");
        System.out.println(Euler_totient_function(i));
    }
}
}

// This code is contributed by rishavmahato348

Python3

# python program for the above approach
import math
def Euler_totient_function(n):
    result = 1
    for i in range(2,n+1):
        c = 0
        if n % i == 0:
            while (n % i == 0):
                c+=1
                n //= i
        if (c > 0):
            power = math.pow(i,c-1)
            m = math.pow(i,c-1)*(i-1)
            result*=m
    if (n > 1):
        result *= (n - 1)
    return int(result)


for i in range(1,13):
    print("Euler_totient_function(" , i , "): ",end="")
    print(Euler_totient_function(i))

C#

// C# program for the above approach
using System;

class GFG {

    static long Euler_totient_function(long n)
    {
        long result = 1;
        for (long i = 2; i * i <= n; i++) {
            long c = 0;
            if (n % i == 0) {
                while (n % i == 0) {
                    c++;
                    n /= i;
                }
            }
            if (c > 0) {
                long sm
                    = (long)Math.Pow(i, c - 1) * (i - 1);
                result *= sm;
            }
        }
        if (n > 1) {
            result *= (n - 1);
        }
        return result;
    }

    // Driver code
    public static void Main()
    {
        for (long i = 1; i < 13; i++) {
            Console.Write("Euler_totient_function(" + i
                          + "): ");
            Console.WriteLine(Euler_totient_function(i));
        }
    }
}

// This code is contributed by rishavmahato348

Javascript

<script>
// Javascript program for the above approach

function Euler_totient_function(n)
{
    let result = 1;
    for (let i = 2; i * i <= n; i++) {
        let c = 0;
        if (n % i == 0) {
            while (n % i == 0) {
                c++;
                n = parseInt(n / i);
            }
        }
        if (c > 0) {
            let power = Math.pow(i, c - 1);
            let sm = Math.pow(i, c - 1) * (i - 1);
            result *= sm;
        }
    }
    if (n > 1) {
        result *= (n - 1);
    }
    return result;
}

// driver code
    for (let i = 1; i < 13; i++) {
        document.write("Euler_totient_function(" + i + "): ");
        document.write(Euler_totient_function(i) + "<br>");
    }

// This code is contributed by subham348.
</script>

Output

Euler_totient_function(1): 1
Euler_totient_function(2): 1
Euler_totient_function(3): 2
Euler_totient_function(4): 2
Euler_totient_function(5): 4
Euler_totient_function(6): 2
Euler_totient_function(7): 6
Euler_totient_function(8): 4
Euler_totient_function(9): 6
Euler_totient_function(10): 4
Euler_totient_function(11): 10
Euler_totient_function(12): 4

Time Complexity: O(sqrt(n)*log(n))

Auxiliary Space: O(1)

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above