Divide an isosceles triangle in two parts with ratio of areas as n:m
Last Updated :
27 Aug, 2022
Given the height 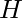 of an isosceles triangle and two integers
of an isosceles triangle and two integers 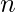 ,
, 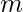 . The task is to find the height
. The task is to find the height 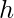 from top of the triangle such that if we make a cut at height h from top parallel to base then the triangle must be divided into two parts with the ratio of their areas equal to n:m.
from top of the triangle such that if we make a cut at height h from top parallel to base then the triangle must be divided into two parts with the ratio of their areas equal to n:m.
Examples:
Input : H = 4, n = 1, m = 1
Output : 2.82843
Input : H = 4, n = 1, m = 0
Output : 4
First of all before proceeding let us mention some of the basic properties of an isosceles triangle.
Let ?ABC is an isosceles triangle with AB = AC and BC being unequal side and base of the triangle. If D is mid-point of BC, then AD is our height H. Also, if we draw a parallel line to BC which cuts AB and AC at points E and F respectively and G being the midpoint of EF then ?AEG is similar to ?ABD, ?AFG is similar to ?ACD, ?AEF is similar to ?ABC, and by using properties of similar triangles we can conclude the following points:
AE/AB = AG/AD = EG/BD = EF/BC = AF/AC —–(i)

As per problem’s requirement, we have to find out the height h, such that the ratio of the area of ?AEF to the area of trapezium EFCB = n:m.
Let, h is the height of cut from the top of the triangle.
Now, area of ?AEF = 0.5 * AG * EF and area of trapezium EFCB = 0.5 * GD * (EF+BC)
also, ratio of both is n:m.
So, we can say that ratio of area of ?AEF to area of ?ABC is equal to n :(n+m).
=> area of ?AEF / area of ?ABC = n / (n+m)
=> (0.5 * AG * EF) / (0.5 * AD * BC) = n / (n+m)
=> (AG/AD) * (EF/BC) = n / (n+m)
=> (EF/BC) * (EF/BC) = n / (n+m)
=> h2 /H2 = n / (n+m)
=> h = H*sqrt(n/(n+m))
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float heightCalculate(int H, int n, int m)
{
float N = n * 1.0;
float M = m * 1.0;
float h = H * sqrt(N / (N + M));
return h;
}
int main()
{
int H = 10, n = 3, m = 4;
cout << heightCalculate(H, n, m);
return 0;
}
|
Java
import java.io.*;
class GFG {
static float heightCalculate(int H, int n, int m)
{
float N = (float)(n * 1.0);
float M = (float)(m * 1.0);
float h = H *(float) Math.sqrt(N / (N + M));
return h;
}
public static void main (String[] args) {
int H = 10, n = 3, m = 4;
System.out.print( heightCalculate(H, n, m));
}
}
|
Python3
from math import sqrt
def heightCalculate(H, n, m):
N = n * 1.0
M = m * 1.0
h = H * sqrt(N / (N + M))
return h
if __name__ == '__main__':
H = 10
n = 3
m = 4
print("{0:.6}" .
format(heightCalculate(H, n, m)));
|
C#
using System;
class GFG
{
static float heightCalculate(int H,
int n, int m)
{
float N = (float)(n * 1.0);
float M = (float)(m * 1.0);
float h = H * (float) Math.Sqrt(N / (N + M));
return h;
}
public static void Main ()
{
int H = 10, n = 3, m = 4;
Console.WriteLine(heightCalculate(H, n, m));
}
}
|
PHP
<?php
function heightCalculate($H, $n, $m)
{
$N = $n * 1.0;
$M = $m * 1.0;
$h = $H * sqrt($N / ($N + $M));
return $h;
}
$H = 10; $n = 3; $m = 4;
echo heightCalculate($H, $n, $m);
?>
|
Javascript
<script>
function heightCalculate(H, n, m)
{
let N = n * 1.0;
let M = m * 1.0;
let h = H * Math.sqrt(N / (N + M));
return h;
}
let H = 10, n = 3, m = 4;
document.write(heightCalculate(H, n, m));
</script>
|
Time Complexity: O(log(n)) as it is using inbuilt sqrt function
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...