Distance Matrix by GPU in R Programming
Last Updated :
27 Apr, 2021
Distance measurement is a vital tool in statistical analysis. It quantifies dissimilarity between sample data for numerical computation. One of the popular choices of distance metric is the Euclidean distance, which is the square root of the sum of squares of attribute differences. In particular, for two data points p and q with n numerical attributes, the Euclidean distance between them is:
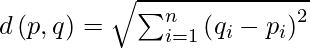
Available distance measures are (written for two vectors x and y)
- Euclidean: Usual distance between the two vectors (2 norms aka L2): √∑i(xi−yi)2
- Maximum: Maximum distance between two components of x and y (supremum norm)
- Manhattan: Absolute distance between the two vectors (1 norm aka L1), ∑Ni=1|Pi−Qi|
- Canberra: Terms with zero numerators and denominators are omitted from the sum and treated as if the values were missing: ∑i|xi−yi|/(|xi|+|yi|)
- Binary (aka asymmetric binary): The vectors are regarded as binary bits, so non-zero elements are ‘on’ and zero elements are ‘off’. The distance is the proportion of bits in which the only one is on amongst those in which at least one is on.
- Minkowski: The p norm, the pth root of the sum of the pth powers of the differences of the components: ∑Ni=1|Pi−Qi|p)1/p
Implementation in R
For computing distance matrix by GPU in R programming, we can use the dist() function. dist() function computes and returns the distance matrix computed by using the specified distance measure to compute the distances between the rows of a data matrix.
Syntax:
dist(x, method = “euclidean”, diag = FALSE, upper = FALSE, p = 2)
Parameters:
x: a numeric matrix, data frame or “dist” object
method: the distance measure to be used. This must be one of “euclidean”, “maximum”, “manhattan”, “canberra”, “binary” or “minkowski”. Any unambiguous substring can be given.
diag: logical value indicating whether the diagonal of the distance matrix should be printed by print.dist.
upper: logical value indicating whether the upper triangle of the distance matrix should be printed by print.dist.
p: The power of the Minkowski distance
Example
R
x <- matrix(rnorm(150), nrow = 5)
dist(x)
dist(x, diag = TRUE)
dist(x, upper = TRUE)
m <- as.matrix(dist(x))
d <- as.dist(m)
stopifnot(d == dist(x))
x <- c(0, 0, 1, 1, 1, 1)
y <- c(1, 0, 1, 1, 0, 1)
dist(rbind(x, y), method = "binary")
dist(rbind(x, y), method = "canberra")
dist(rbind(x, y), method = "manhattan")
dist(rbind(x, y), method = "euclidean")
dist(rbind(x, y), method = "maximum")
dist(rbind(x, y), method = "minkowski")
|
Output:
> dist(x)
1 2 3 4
2 6.772630
3 7.615303 7.390410
4 6.460424 6.759275 7.773421
5 6.551426 7.688254 7.886380 7.039102
> dist(x, diag = TRUE)
1 2 3 4 5
1 0.000000
2 6.772630 0.000000
3 7.615303 7.390410 0.000000
4 6.460424 6.759275 7.773421 0.000000
5 6.551426 7.688254 7.886380 7.039102 0.000000
> dist(x, upper = TRUE)
1 2 3 4 5
1 6.772630 7.615303 6.460424 6.551426
2 6.772630 7.390410 6.759275 7.688254
3 7.615303 7.390410 7.773421 7.886380
4 6.460424 6.759275 7.773421 7.039102
5 6.551426 7.688254 7.886380 7.039102
> dist(rbind(x, y), method = "binary")
x
y 0.4
> dist(rbind(x, y), method = "canberra")
x
y 2.4
> dist(rbind(x, y), method = "manhattan")
x
y 2
> dist(rbind(x, y), method = "euclidean")
x
y 1.414214
> dist(rbind(x, y), method = "maximum")
x
y 1
> dist(rbind(x, y), method = "minkowski")
x
y 1.414214
Share your thoughts in the comments
Please Login to comment...