Design Mod – N synchronous Counter
Last Updated :
18 Oct, 2022
The value of N can be different from power of 2. Also, the counting sequence may be random for example some cyclic code (8421, 2423 etc). The following method is applied for designing for mod N and any counting sequence.
Design for Mod-N counter :
The steps for the design are –
Step 1 : Decision for number of flip-flops –
Example : If we are designing mod N counter and n number of flip-flops are required then n can be found out by this equation.
N <= 2n
Here we are designing Mod-10 counter Therefore, N= 10 and number of Flip flops(n) required is
For n =3, 10<=8, which is false.
For n= 4,10<=16, which is true.
Therefore number of FF required is 4 for Mod-10 counter.
Step 2 : Write excitation table of Flip flops –
Here T FF is used
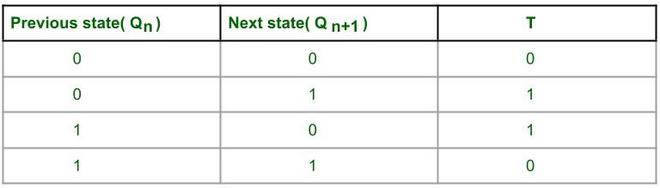
Excitation table of T FF.
Step 3 : Draw state diagram and circuit excitation table –

Counting Sequence of Decade counter
A decade counter is called as mod -10 or divide by 10 counter. It counts from 0 to 9 and again reset to 0. It counts in natural binary sequence. Here 4 T Flip flops are used. It resets after Q3 Q2 Q1 Q0 = 1001.
Circuit excitation table –
Here Q3 Q2 Q1 Q0 are present states of four flip-flops and Q*3 Q*2 Q*1 Q*0 are next counting state of 4 Flip flops. If there is a transition in current state i.e if Q3 value changes from 0 to 1 or 1 to 0 then there’s corresponding T(toggle) bit is written as 1 otherwise 0.

Circuit excitation table
Step 4 : Create Karnaugh map for each FF input in terms of flip-flop outputs as the input variable –
Simplify the K map –

K map for finding minimal expressions.
Step 5 : Create circuit diagram –
Here negative edge triggered clock is used for toggling purpose.
- The clock is provided to every Flip flop at same instant of time.
- The toggle(T) input is provided to every Flip flop according to the simplified equation of K map.

Circuit diagram
Timing diagram : Here toggling is used.

Characteristic table of T FF.
The state of a FF will change only when toggle input(T) of a FF is 1.

Timing diagram of synchronous Decade counter
Explanation :
- Initially Q3 Q2 Q1 Q0 are 0 0 0 0.
- The sequence of counter can be verified from the timing diagram. At every falling edge of the clock output Q0 toggles because T0 is connected to logic 1.
- T1 becomes 1 only when expression T1 = Q’3Q0 becomes 1 also if clock falling edge occurs(because there is negative edge triggering) then the output state of T1 i.e Q1 will change.
- T2 becomes 1 only when expression T2 = Q1Q0 becomes 1 also if clock falling edge occurs then the output state Q2 will change.
- T3 becomes 1 only when expression T1 = Q3Q0 + Q2Q1Q0 resultant becomes 1 also if clock falling edge occurs(because there is negative edge triggering) then the state of Q3 will change.
- We get Output as Q3(MSB) Q2 Q1 Q0(LSB).
- After 10th falling edge the output state of all the FFs again becomes 0 0 0 0.
Share your thoughts in the comments
Please Login to comment...