Count the total number of squares that can be visited by Bishop in one move
Last Updated :
15 Sep, 2022
Given the position of a Bishop on an 8 * 8 chessboard, the task is to count the total number of squares that can be visited by the Bishop in one move. The position of the Bishop is denoted using row and column number of the chessboard.
Examples:
Input: Row = 4, Column = 4
Output: 13
Input: Row = 1, Column = 1
Output: 7
Approach: In the game of chess, a Bishop can only move diagonally and there is no restriction in distance for each move.
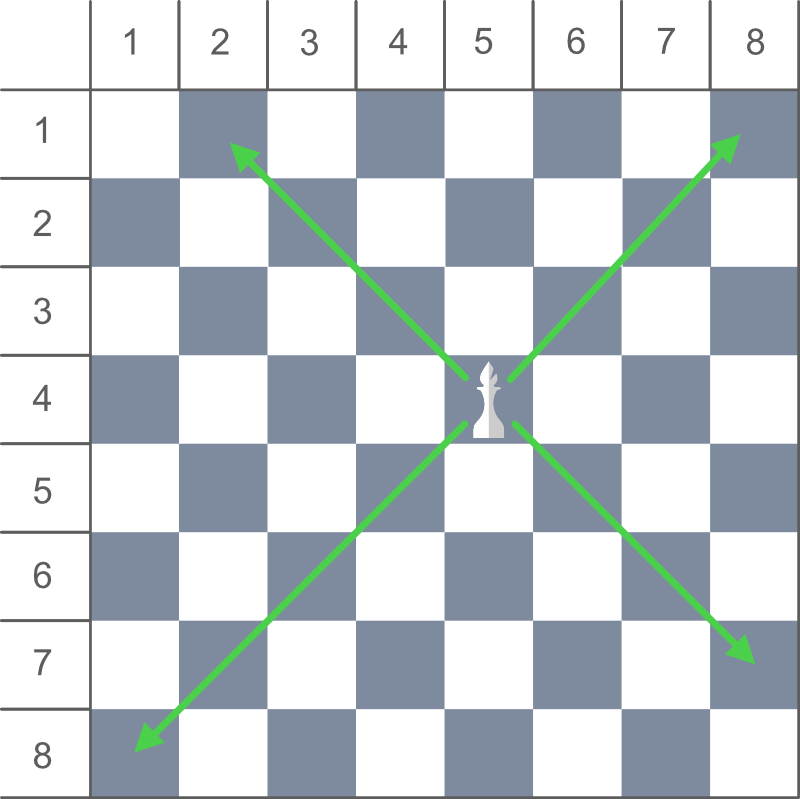
So, We can also say that Bishop can move in four ways i.e. diagonally top left, top right, bottom left and bottom right from current position.
We can calculate the numbers of squares visited in each move by:
Total squares visited in Top Left move = min(r, c) – 1
Total squares visited in Top Right move = min(r, 9 – c) – 1
Total squares visited in Bottom Left move = 8 – max(r, 9 – c)
Total squares visited in Bottom Right move = 8 – max(r, c)
where, r and c are the coordinates of the current position of the Bishop on the chessboard.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countSquares(int row, int column)
{
int topLeft = min(row, column) - 1;
int bottomRight = 8 - max(row, column);
int topRight = min(row, 9 - column) - 1;
int bottomLeft = 8 - max(row, 9 - column);
return (topLeft + topRight + bottomRight + bottomLeft);
}
int main()
{
int row = 4, column = 4;
cout << countSquares(row, column);
return 0;
}
|
Java
class GFG {
static int countSquares(int row, int column)
{
int topLeft = Math.min(row, column) - 1;
int bottomRight = 8 - Math.max(row, column);
int topRight = Math.min(row, 9 - column) - 1;
int bottomLeft = 8 - Math.max(row, 9 - column);
return (topLeft + topRight + bottomRight + bottomLeft);
}
public static void main(String[] args)
{
int row = 4, column = 4;
System.out.println(countSquares(row, column));
}
}
|
C#
using System;
class GFG {
static int countSquares(int row, int column)
{
int topLeft = Math.Min(row, column) - 1;
int bottomRight = 8 - Math.Max(row, column);
int topRight = Math.Min(row, 9 - column) - 1;
int bottomLeft = 8 - Math.Max(row, 9 - column);
return (topLeft + topRight + bottomRight + bottomLeft);
}
public static void Main()
{
int row = 4, column = 4;
Console.WriteLine(countSquares(row, column));
}
}
|
Python3
def countSquares(row, column):
topLeft = min(row, column) - 1
bottomRight = 8 - max(row, column)
topRight = min(row, 9-column) -1
bottomLeft = 8 - max(row, 9-column)
return (topLeft + topRight + bottomRight + bottomLeft)
row = 4
column = 4
print(countSquares(row, column))
|
PHP
<?php
function countSquares($row, $column)
{
$topLeft = min($row, $column) - 1;
$bottomRight = 8 - max($row, $column);
$topRight = min($row, 9 - $column) - 1;
$bottomLeft = 8 - max($row, 9 - $column);
return ($topLeft + $topRight +
$bottomRight + $bottomLeft);
}
$row = 4;
$column = 4;
echo countSquares($row, $column);
?>
|
Javascript
<script>
function countSquares(row, column)
{
var topLeft = Math.min(row, column) - 1;
var bottomRight = 8 - Math.max(row, column);
var topRight = Math.min(row, 9 - column) - 1;
var bottomLeft = 8 - Math.max(row, 9 - column);
return (topLeft + topRight + bottomRight + bottomLeft);
}
var row = 4, column = 4;
document.write( countSquares(row, column));
</script>
|
Complexity Analysis:
- Time Complexity: O(1)
- Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...