Count ways to place Knights moving in L shape in chessboard
Last Updated :
23 Sep, 2022
Given two integers, N and M, denoting dimensions of a chessboard. The task is to count ways to place a black and a white knight on an N * M chessboard such that they do not attack each other the knights have to be placed on different squares.
Note: A knight can move two squares horizontally and one square vertically (L shaped), or two squares vertically and one square horizontally (L shaped). The knights attack each other if one can reach the other in one move.
Examples:
Input: N=2, M=2
Output: 12
Explanation: Black and a white knight can be placed in 12 possible ways such that none of them attracts each other.
Input: N=2, M=3
Output: 26
Naive Approach:
For each cell count number of ways the knights can be placed so that both can attack each other and then subtract the count from the total arrangements.
Below is the idea to solve the problem:
- Total arrangements can be calculated as:
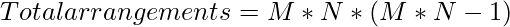 because for each cell we can place other knight at (M * N – 1) cells and the total M * N cell will be there.
because for each cell we can place other knight at (M * N – 1) cells and the total M * N cell will be there. - Run for loop for every cell(i, j) of the chess board and check if any of the (i-2, j+1), (i-1, j+2), (i+1, j+2), and (i+2, j+1) cells lies on the chessboard then increment the number of possible combinations by one.
Below is the Implementation of the above approach:
C++
#include <iostream>
using namespace std;
long long Solve(int n, int m)
{
int X_axis[]{ -2, -1, 1, 2 };
int Y_axis[]{ 1, 2, 2, 1 };
long long ret = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 4; ++k) {
int x = i + X_axis[k], y = j + Y_axis[k];
if (x >= 0 && x < m && y >= 0 && y < n)
++ret;
}
}
}
long long Total = m * n;
Total = Total * (Total - 1) / 2;
return 2 * (Total - ret);
}
int main()
{
int N = 2, M = 3;
cout << Solve(N, M) << endl;
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static long Solve(int n, int m)
{
int X_axis[] = { -2, -1, 1, 2 };
int Y_axis[] = { 1, 2, 2, 1 };
long ret = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 4; ++k) {
int x = i + X_axis[k];
int y = j + Y_axis[k];
if (x >= 0 && x < m && y >= 0 && y < n)
++ret;
}
}
}
long Total = m * n;
Total = Total * (Total - 1) / 2;
return 2 * (Total - ret);
}
public static void main(String[] args)
{
int N = 2, M = 3;
System.out.println(Solve(N, M));
}
}
|
Python3
def Solve(n, m):
X_axis = []
X_axis = [-2, -1, 1, 2]
Y_axis = []
Y_axis = [1, 2, 2, 1]
ret = 0
for i in range(m):
for j in range(n):
for k in range(4):
x = i + X_axis[k]
y = j + Y_axis[k]
if (x >= 0 and x < m and
y >= 0 and y < n):
ret += 1
Total = m * n
Total = Total * (Total - 1) // 2
return 2 * (Total - ret)
N = 2
M = 3
print(Solve(N, M))
|
C#
using System;
class GFG {
static long Solve(int n, int m)
{
int[] X_axis = { -2, -1, 1, 2 };
int[] Y_axis = { 1, 2, 2, 1 };
long ret = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 4; ++k) {
int x = i + X_axis[k];
int y = j + Y_axis[k];
if (x >= 0 && x < m && y >= 0 && y < n)
++ret;
}
}
}
long Total = m * n;
Total = Total * (Total - 1) / 2;
return 2 * (Total - ret);
}
public static void Main(String[] args)
{
int N = 2, M = 3;
Console.Write(Solve(N, M));
}
}
|
Javascript
<script>
function Solve(n, m)
{
let X_axis = [ -2, -1, 1, 2];
let Y_axis = [ 1, 2, 2, 1 ];
let ret = 0;
for (let i = 0; i < m; ++i)
{
for (let j = 0; j < n; ++j)
{
for (let k = 0; k < 4; ++k)
{
let x = i + X_axis[k],
y = j + Y_axis[k];
if (x >= 0 && x < m
&& y >= 0 && y < n)
++ret;
}
}
}
let Total = m * n;
Total = Total * (Total - 1) / 2;
return 2 * (Total - ret);
}
let N = 2, M = 3;
document.write(Solve(N, M));
</script>
|
Time complexity: O(N * M)
Auxiliary Space: O(1).
Efficient Approach:
The arrangements in this case where knight to move 2 steps in the horizontal direction and 1 step in the vertical. where attack is possible are equal to 4 * (N – 2) * (M – 1) and similarly for 2 steps in the vertical direction and 1 step in the horizontal. Thus the answer will be Total possible arrangement – 4 * (N – 2) * (M – 1) – 4 * (N – 1) * (M – 2).
Follow the below steps to Implement the idea:
- Suppose the board has N rows and M columns. Now first consider knight to move 2 steps in the horizontal direction and 1 step in the vertical. So if we are at (i, j) after such moves we can reach at (i+2, j+1), (i+2, j-1), (i-2, j+1), (i-2, j-1).To have (i+2) inside the board we can have our positions 0 to N-3 i.e we have to leave the last two rows otherwise (i+2) will be out of the board. similarly for (i-2) range is possible if 2 to N-1.
- Similarly for (j+1) range will be 0 to M-2, and for (j-1) range will be 1 to M-1 i.e one column less in each case.
- So, arrangements in this case where attack possible equal to 4 * (N – 2) * (M – 1)
- Similarly, if we consider two steps in vertical and one step in horizontal we will have one less row and two less col so that two knights can attack each other.
- We will subtract this arrangement from total arrangements which is M * N * (M * N – 1).
- Hence the answer will be M * N * (M * N – 1) – 4 * (N – 2) * (M – 1) – 4 * (N – 1) * (M – 2)
Below is the Implementation of the above approach:
C++
#include <iostream>
using namespace std;
long long Solve(int N, int M)
{
int ans = (N * M - 1) * N * M;
if (N >= 1 && M >= 2) {
ans -= (4 * (N - 1) * (M - 2));
}
if (N >= 2 && M >= 1) {
ans -= (4 * (N - 2) * (M - 1));
}
return ans;
}
int main()
{
int N = 2, M = 3;
cout << Solve(N, M) << endl;
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static long Solve(int N, int M)
{
long ans = (N * M - 1) * N * M;
if (N >= 1 && M >= 2) {
ans -= (4 * (N - 1) * (M - 2));
}
if (N >= 2 && M >= 1) {
ans -= (4 * (N - 2) * (M - 1));
}
return ans;
}
public static void main(String[] args)
{
int N = 2, M = 3;
System.out.println(Solve(N, M));
}
}
|
Python3
def Solve(N, M):
ans = (N * M - 1) * N * M
if (N >= 1 and M >= 2):
ans -= (4 * (N - 1) * (M - 2))
if (N >= 2 and M >= 1):
ans -= (4 * (N - 2) * (M - 1))
return ans
N = 2
M = 3
print(Solve(N, M))
|
C#
using System;
class GFG {
static long Solve(int N, int M)
{
int ans = (N * M - 1) * N * M;
if (N >= 1 && M >= 2) {
ans -= (4 * (N - 1) * (M - 2));
}
if (N >= 2 && M >= 1) {
ans -= (4 * (N - 2) * (M - 1));
}
return ans;
}
static public void Main()
{
int N = 2, M = 3;
Console.Write(Solve(N, M));
}
}
|
Javascript
<script>
function Solve(N, M)
{
let ans = (N * M - 1) * N * M;
if (N >= 1 && M >= 2)
{
ans -= (4 * (N - 1) * (M - 2));
}
if (N >= 2 && M >= 1)
{
ans -= (4 * (N - 2) * (M - 1));
}
return ans;
}
let N = 2, M = 3;
document.write(Solve(N, M));
</script>
|
Time Complexity: O(1).
Auxiliary Space: O(1).
Share your thoughts in the comments
Please Login to comment...