Count squares possible from M and N straight lines parallel to X and Y axis respectively
Last Updated :
28 Dec, 2022
Given two arrays X[] and Y[] consisting of N and M integers such that there are N lines parallel to the y-axis and M lines parallel to the x-axis. The task is to find the total number of squares formed by these lines on a coordinate plane.
Each integer(say a) in the array X[] denotes lines having equation x = a, parallel to y-axis.
Each integer(say b) in the array Y[] denotes lines having equation y = b, parallel to x-axis.
Examples:
Input: N = 3, M = 4, X[] = {1, 3, 7}, Y[] = {2, 4, 6, 1}
Output: 3
Explanation:
3 lines are parallel to y-axis for x = 1, x = 3 and x = 7.
4 lines are parallel to x-axis for y = 2, y = 4, y = 6 and y = 1.
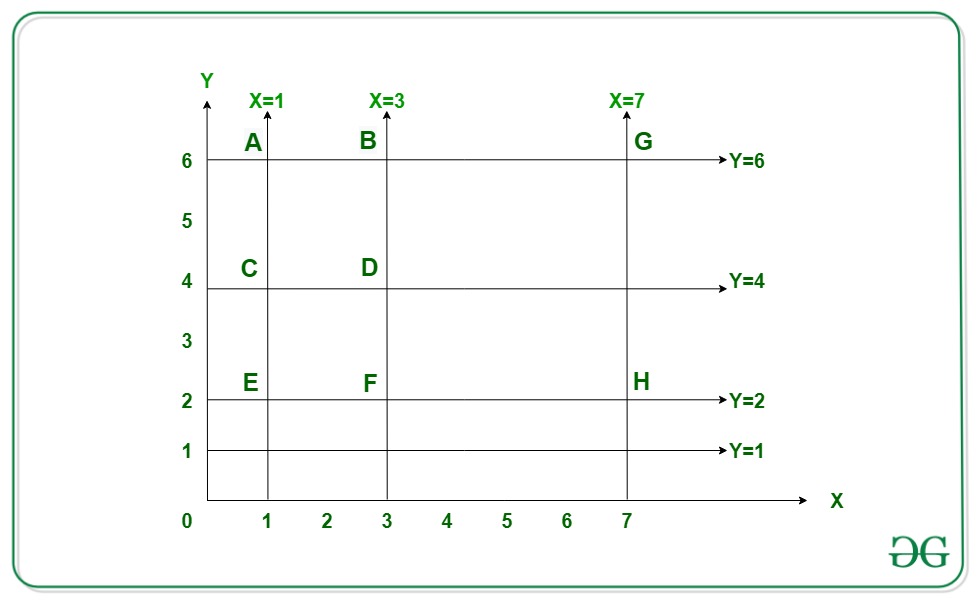
From the above image, below are three possible squares formed:
1) square CDEF (x = 1, x = 3, y = 2, y = 4), side = 2 units.
2) square ABDC (x = 1, x = 3, y = 4, y = 6), side = 2 units.
3) square BGHF (x = 3, x = 7, y = 2, y = 6), side = 4 units.
Input: N = 5, M = 4, X[] = {1, 9, 2, 3, 7}, Y[] = {1, 2, 4, 6}
Output: 8
Approach: Follow the steps below to solve the problem:
- Find the distance between all pairs in X[] array and store the count in a Map, say M1.
- Find the distance between all pairs in Y[] array and store the count in a Map M2.
- If the distance of pairs of M1 is present in M2, then a square can be made by using both the pairs.
- Therefore, the total count of squares can be calculated by adding all the counts of distances stored in M1 as well as in M2.
- Print the total count of squares after completing the above steps.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int numberOfSquares(int X[], int Y[],
int N, int M)
{
unordered_map<int, int> m1, m2;
int i, j, ans = 0;
for (i = 0; i < N; i++) {
for (j = i + 1; j < N; j++) {
int dist = abs(X[i] - X[j]);
m1[dist]++;
}
}
for (i = 0; i < M; i++) {
for (j = i + 1; j < M; j++) {
int dist = abs(Y[i] - Y[j]);
m2[dist]++;
}
}
for (auto i = m1.begin();
i != m1.end(); i++) {
if (m2.find(i->first)
!= m2.end()) {
ans += (i->second
* m2[i->first]);
}
}
return ans;
}
int main()
{
int X[] = { 1, 3, 7 };
int Y[] = { 2, 4, 6, 1 };
int N = sizeof(X) / sizeof(X[0]);
int M = sizeof(Y) / sizeof(Y[0]);
cout << numberOfSquares(X, Y, N, M);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG{
static int numberOfSquares(int[] X, int[] Y, int N,
int M)
{
HashMap<Integer,
Integer> m1 = new HashMap<Integer,
Integer>();
HashMap<Integer,
Integer> m2 = new HashMap<Integer,
Integer>();
int i, j, ans = 0;
for(i = 0; i < N; i++)
{
for(j = i + 1; j < N; j++)
{
int dist = Math.abs(X[i] - X[j]);
m1.put(dist, m1.getOrDefault(dist, 0) + 1);
}
}
for(i = 0; i < M; i++)
{
for(j = i + 1; j < M; j++)
{
int dist = Math.abs(Y[i] - Y[j]);
m2.put(dist, m2.getOrDefault(dist, 0) + 1);
}
}
for(Map.Entry<Integer,
Integer> entry : m1.entrySet())
{
if (m2.containsKey(entry.getKey()))
{
ans += (entry.getValue() *
m2.get(entry.getKey()));
}
}
return ans;
}
public static void main(String[] args)
{
int X[] = { 1, 3, 7 };
int Y[] = { 2, 4, 6, 1 };
int N = X.length;
int M = Y.length;
System.out.println(numberOfSquares(X, Y, N, M));
}
}
|
Python3
def numberOfSquares(X, Y, N, M):
m1 = {}
m2 = {}
ans = 0
for i in range(0, N):
for j in range(i + 1, N):
dist = abs(X[i] - X[j])
if dist in m1:
m1[dist] = m1[dist] + 1
else:
m1[dist] = 1
for i in range(0, M):
for j in range(i + 1, M):
dist = abs(Y[i] - Y[j])
if dist in m2:
m2[dist] = m2[dist] + 1
else:
m2[dist] = 1
for key in m1:
if key in m2:
ans = ans + (m1[key] * m2[key])
return ans
if __name__ == "__main__":
X = [ 1, 3, 7 ]
Y = [ 2, 4, 6, 1 ]
N = len(X)
M = len(Y)
print(numberOfSquares(X, Y, N, M))
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int numberOfSquares(int[] X, int[] Y, int N,
int M)
{
Dictionary<int,
int> m1 = new Dictionary<int,
int>();
Dictionary<int,
int> m2 = new Dictionary<int,
int>();
int i, j, ans = 0;
for(i = 0; i < N; i++)
{
for(j = i + 1; j < N; j++)
{
int dist = Math.Abs(X[i] - X[j]);
if (m1.ContainsKey(dist))
m1[dist]++;
else
m1.Add(dist, 1);
}
}
for(i = 0; i < M; i++)
{
for(j = i + 1; j < M; j++)
{
int dist = Math.Abs(Y[i] - Y[j]);
if (m2.ContainsKey(dist))
m2[dist]++;
else
m2.Add(dist, 1);
}
}
foreach(KeyValuePair<int, int> entry in m1)
{
if (m2.ContainsKey(entry.Key))
{
ans += (entry.Value *
m2[entry.Key]);
}
}
return ans;
}
public static void Main()
{
int[] X = { 1, 3, 7 };
int[] Y = { 2, 4, 6, 1 };
int N = X.Length;
int M = Y.Length;
Console.WriteLine(numberOfSquares(X, Y, N, M));
}
}
|
Javascript
<script>
function numberOfSquares(X, Y, N, M)
{
var m1 = new Map(), m2 = new Map();
var i, j, ans = 0;
for (i = 0; i < N; i++) {
for (j = i + 1; j < N; j++) {
var dist = Math.abs(X[i] - X[j]);
if(m1.has(dist))
m1.set(dist, m1.get(dist)+1)
else
m1.set(dist, 1);
}
}
for (i = 0; i < M; i++) {
for (j = i + 1; j < M; j++) {
var dist = Math.abs(Y[i] - Y[j]);
if(m2.has(dist))
m2.set(dist, m2.get(dist)+1)
else
m2.set(dist, 1);
}
}
m1.forEach((value, key) => {
if (m2.has(key)) {
ans += (value
* m2.get(key));
}
});
return ans;
}
var X = [1, 3, 7];
var Y = [2, 4, 6, 1];
var N = X.length;
var M = Y.length;
document.write( numberOfSquares(X, Y, N, M));
</script>
|
Time Complexity: O(M2+ N2)
Auxiliary Space: O(M2+ N2)
Share your thoughts in the comments
Please Login to comment...