Count points from an array that lies inside a semi-circle
Last Updated :
28 May, 2021
Given two pairs (X, Y), (P, Q) and R the coordinate of the center of semi-circle, coordinate of the intersection of semicircle and diameter of the semicircle and, the radius of the semicircle, and an array arr[] of dimension N*2 consisting of the coordinates of few points, the task is to find the number of points from the array that lies inside or on the
semicircle.
Note: The semicircle above the diameter is considered.
Examples:
Input: X = 0, Y = 0, R = 5, P = 5, Q = 0, arr[][] = { {2, 3}, {5, 6}, {-1, 4}, {5, 5} }
Output: 2
Explanation: The points {2, 3} and {-1, 4} are inside the semi-circle.

Input: X = 2, Y = 3, R = 10, P = 12, Q = 3, arr[][] = { {-7, -5}, {0, 6}, {11, 4} }
Output: 2
Approach: The given problem can be solved based on the following observations:
- The points that lies on or inside the semicircle must be above or on the diameter of semicircle and the distance between center and that point should be ? R.
- Suppose
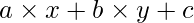 is the equation of diameter.
is the equation of diameter.
The point (R, S) lies above the line if
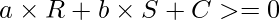
- A point (R, S) lies above the line formed by joining points (X, Y) and (P, Q) if
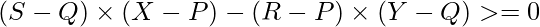
Follow the steps below to solve the problem:
- Find the equation of line the diameter of the semi-circle from the points (X, Y) and (P, Q).
- Initialize a variable, say ans, to store the count of required points.
- Traverse the array arr[] and perform the following operations:
- Calculate the distance between the points (X, Y) and (P, Q) and store it in a variable, say d.
- Put arr[i][0] and arr[i][1] in the place of R and S respectively, in the formula
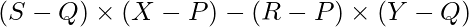
and store the result in a variable, say f. - Increment the count of ans by 1 if R ? d and f ? 0.
- After completing the above steps, print the value stored in ans.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int getPointsIns(int x1, int y1, int radius, int x2,
int y2, vector<pair<int, int>> points)
{
int ans = 0;
for(int i = 0; i < points.size(); i++)
{
bool condOne = false, condTwo = false;
if ((points[i].second - y2) *
(x2 - x1) - (y2 - y1) *
(points[i].first - x2) >= 0)
{
condOne = true;
}
if (radius >= (int)sqrt(pow((y1 - points[i].second), 2) +
pow(x1 - points[i].first, 2)))
{
condTwo = true;
}
if (condOne && condTwo)
{
ans += 1;
}
}
return ans;
}
int main()
{
int X = 0;
int Y = 0;
int R = 5;
int P = 5;
int Q = 0;
vector<pair<int, int>> arr = { make_pair(2, 3),
make_pair(5, 6),
make_pair(-1, 4),
make_pair(5, 5) };
cout << getPointsIns(X, Y, R, P, Q, arr);
return 0;
}
|
Java
import java.io.*;
class Gfg {
public static int getPointsIns(int x1, int y1,int radius,
int x2,int y2, pair points[])
{
int ans = 0;
for (int i = 0; i < points.length; i++)
{
boolean condOne = false, condTwo = false;
if ((points[i].b - y2) *
(x2 - x1)- (y2 - y1) *
(points[i].a - x2)>= 0)
{
condOne = true;
}
if (radius >= (int)Math.sqrt(Math.pow((y1 - points[i].b), 2)+
Math.pow(x1 - points[i].a, 2)))
{
condTwo = true;
}
if (condOne && condTwo)
{
ans += 1;
}
}
return ans;
}
public static void main(String[] args)
{
int X = 0;
int Y = 0;
int R = 5;
int P = 5;
int Q = 0;
pair arr[] = {new pair(2, 3), new pair(5, 6), new pair(-1, 4), new pair(5,5)};
System.out.print(getPointsIns(X, Y, R, P, Q, arr));
}
}
class pair
{
int a;
int b;
pair(int a,int b)
{
this.a = a;
this.b = b;
}
}
|
Python3
def getPointsIns(x1, y1, radius, x2, y2, points):
ans = 0
for point in points:
condOne = (point[1] - y2) * (x2 - x1) \
- (y2 - y1) * (point[0] - x2) >= 0
condTwo = radius >= ((y1 - point[1]) ** 2 \
+ (x1 - point[0]) ** 2) ** (0.5)
if condOne and condTwo:
ans += 1
return ans
X = 0
Y = 0
R = 5
P = 5
Q = 0
arr = [[2, 3], [5, 6], [-1, 4], [5, 5]]
print(getPointsIns(X, Y, R, P, Q, arr))
|
C#
using System;
class Gfg
{
public static int getPointsIns(int x1, int y1,
int radius, int x2,
int y2, pair[] points)
{
int ans = 0;
for (int i = 0; i < points.Length; i++) {
bool condOne = false, condTwo = false;
if ((points[i].b - y2) * (x2 - x1)
- (y2 - y1) * (points[i].a - x2)
>= 0) {
condOne = true;
}
if (radius >= (int)Math.Sqrt(
Math.Pow((y1 - points[i].b), 2)
+ Math.Pow(x1 - points[i].a, 2))) {
condTwo = true;
}
if (condOne && condTwo) {
ans += 1;
}
}
return ans;
}
public static void Main(string[] args)
{
int X = 0;
int Y = 0;
int R = 5;
int P = 5;
int Q = 0;
pair[] arr = { new pair(2, 3), new pair(5, 6),
new pair(-1, 4), new pair(5, 5) };
Console.Write(getPointsIns(X, Y, R, P, Q, arr));
}
}
public class pair {
public int a;
public int b;
public pair(int a, int b)
{
this.a = a;
this.b = b;
}
}
|
Javascript
<script>
function getPointsIns(x1,y1,radius,x2,y2,points)
{
let ans = 0;
for (let i = 0; i < points.length; i++)
{
let condOne = false, condTwo = false;
if ((points[i][1] - y2) *
(x2 - x1)- (y2 - y1) *
(points[i][0] - x2)>= 0)
{
condOne = true;
}
if (radius >= Math.sqrt(Math.pow((y1 - points[i][1]), 2)+
Math.pow(x1 - points[i][0], 2)))
{
condTwo = true;
}
if (condOne && condTwo)
{
ans += 1;
}
}
return ans;
}
let X = 0;
let Y = 0;
let R = 5;
let P = 5;
let Q = 0;
let arr = [[2, 3], [5, 6], [-1, 4], [5, 5]];
document.write(getPointsIns(X, Y, R, P, Q, arr));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...